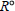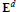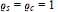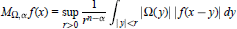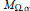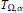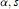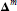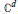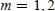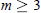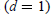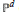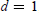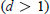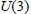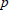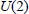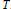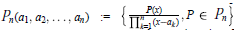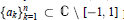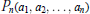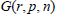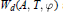Research Article
Subgroups of the Adjoint Group of a Radical Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-15
-
- Article
-
- You have access
- Export citation
Asymptotic Shape of Finite Packings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 16-28
-
- Article
-
- You have access
- Export citation
Weighted Norm Inequalities for Fractional Integral Operators With Rough Kernel
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 29-39
-
- Article
-
- You have access
- Export citation
Green's Functions for Powers of the Invariant Laplacian
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 40-73
-
- Article
-
- You have access
- Export citation
Elementary Proof of the Fundamental Lemma For a Unitary Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 74-98
-
- Article
-
- You have access
- Export citation
Aϕ-Invariant Subspaces on the Torus
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 99-133
-
- Article
-
- You have access
- Export citation
On Critical Level Sets of Some two Degrees of Freedom Integrable Hamiltonian Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 134-151
-
- Article
-
- You have access
- Export citation
Inequalities for Rational Functions With Prescribed Poles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 152-166
-
- Article
-
- You have access
- Export citation
Murnaghan-Nakayama Rules for Characters of Iwahori-Hecke Algebras of the Complex Reflection Groups G(r, p, n)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 167-192
-
- Article
-
- You have access
- Export citation
Intertwining Operator and h-Harmonics Associated With Reflection Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 193-209
-
- Article
-
- You have access
- Export citation
Isomorphisms Between Generalized Cartan Type W Lie Algebras in Characteristic 0
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 210-224
-
- Article
-
- You have access
- Export citation