Research Article
A Characterization of Universal Loeb Measurability for Completely Regular Hausdorff Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-690
-
- Article
-
- You have access
- Export citation
An Application of Homogenization Theory to Harmonic Analysis: Harnack Inequalities And Riesz Transforms on Lie Groups of Polynomial Growth
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 691-727
-
- Article
-
- You have access
- Export citation
Differential Forms and Resolutions on Certain Analytic Spaces II. Flat Resolutions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 728-749
-
- Article
-
- You have access
- Export citation
Continuous Hahn Polynomials of Differential Operator Argument and Analysis on Riemannian Symmetric Spaces of Constant Curvature
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 750-773
-
- Article
-
- You have access
- Export citation
Positive Dependence of Exchangeable Sequences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 774-783
-
- Article
-
- You have access
- Export citation
A Set-Valued Generalization of Fan's Best Approximation Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 784-796
-
- Article
-
- You have access
- Export citation
Bourgain Algebras of Douglas Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 797-804
-
- Article
-
- You have access
- Export citation
Analysis on Sparse Parts in the Maximal Ideal Space of H∞
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 805-823
-
- Article
-
- You have access
- Export citation
Class Numbers of Real Quadratic Fields, Continued Fractions, Reduced Ideals, Prime-Producing Quadratic Polynomials and Quadratic Residue Covers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 824-842
-
- Article
-
- You have access
- Export citation
Dedekind Completeness and the Algebraic Complexity of o-Minimal Structures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 843-855
-
- Article
-
- You have access
- Export citation
Extreme Points of Positive Functionals and Spectral States on Real Banach Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 856-866
-
- Article
-
- You have access
- Export citation
An Addition Theorem and Some Product Formulas for the Hahn-Exton q-Bessel Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 867-879
-
- Article
-
- You have access
- Export citation
Fixed Point Theorem and Nonlinear Ergodic Theorem for Nonexpansive Semigroups Without Convexity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 880-887
-
- Article
-
- You have access
- Export citation
Fixed Point Principles for Cones of a Banach Space for the Multivalued Maps Differentiable at the Origin and Infinity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 888-896
-
- Article
-
- You have access
- Export citation



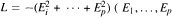 are left invariant Hörmander vector fields) on a connected Lie group
are left invariant Hörmander vector fields) on a connected Lie group 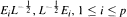 , are bounded on
, are bounded on 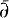 operator. This construction is independent of the one in [1] and apart from the general result of Section 1 of [1], it can be read independently. As in [1], the hypotheses on
operator. This construction is independent of the one in [1] and apart from the general result of Section 1 of [1], it can be read independently. As in [1], the hypotheses on 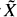 in a desingularization of
in a desingularization of 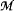 is a Dedekind complete model of
is a Dedekind complete model of 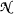 of
of  . In contrast, we show that if
. In contrast, we show that if 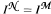 .
.