Research Article
The topological degree of A-proper mapping in the Menger PN-space (I)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-168
-
- Article
-
- You have access
- Export citation
The topological degree of A-proper mapping in the Menger PN-space (II)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-173
-
- Article
-
- You have access
- Export citation
Multiplicity of positive periodic solutions to second order differential equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 175-182
-
- Article
-
- You have access
- Export citation
Pseudo-Einstein real hypersurfaces in complex two-plane Grassmannians
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 183-200
-
- Article
-
- You have access
- Export citation
The joint distribution of the Riemann zeta - function
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 201-217
-
- Article
-
- You have access
- Export citation
On the number of conjugacy classes of normalisers in a finite p-group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 219-230
-
- Article
-
- You have access
- Export citation
Groups acting on a set whose orbits are all singleton
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 231-234
-
- Article
-
- You have access
- Export citation
Products of composition and differentiation between Hardy spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 235-243
-
- Article
-
- You have access
- Export citation
Construction of elliptic curves with cyclic groups over prime fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 245-254
-
- Article
-
- You have access
- Export citation
Reverse inequalities for the numerical radius of linear operators in Hilbert spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 255-262
-
- Article
-
- You have access
- Export citation
Namioka spaces and topological games
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 263-272
-
- Article
-
- You have access
- Export citation
On representations of variants of semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 273-283
-
- Article
-
- You have access
- Export citation
On some generalisations of the Erdős distance problem over finite fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 285-292
-
- Article
-
- You have access
- Export citation
A note on a theorem of F. Wang and G. Tang
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 293-297
-
- Article
-
- You have access
- Export citation
Upper semi continuity of attractors of delay differential equations in the delay
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 299-306
-
- Article
-
- You have access
- Export citation
The generalised f-projection operator with an application
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 307-317
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Small graph designs and their various properties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 319-320
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 73 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 73 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation



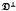 -
-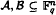 where
where 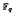 is a finite field of
is a finite field of 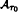 in the space
in the space 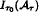 of
of