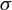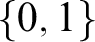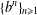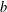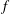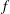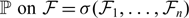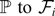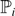21 results in 60Axx
UNPRINCIPLED
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 13 June 2023, pp. 435-474
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Berkelmans–Pries dependency function: A generic measure of dependence between random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 23 March 2023, pp. 1115-1135
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
AXIOMS FOR TYPE-FREE SUBJECTIVE PROBABILITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 493-508
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
A category-theoretic proof of the ergodic decomposition theorem
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 15 February 2023, pp. 4166-4192
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
NECESSARY AND SUFFICIENT CONDITIONS FOR DOMINATION RESULTS FOR PROPER SCORING RULES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 16 January 2023, pp. 132-143
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semantics modulo satisfiability with applications: function representation, probabilities and game theory
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 June 2022, pp. 264-265
- Print publication:
- June 2022
-
- Article
-
- You have access
- Export citation
TOWARDS THE INEVITABILITY OF NON-CLASSICAL PROBABILITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 21 February 2022, pp. 1053-1079
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUPPORT FOR GEOMETRIC POOLING
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 21 October 2020, pp. 298-337
- Print publication:
- March 2023
-
- Article
-
- You have access
- Export citation
PROBABILISTIC STABILITY, AGM REVISION OPERATORS AND MAXIMUM ENTROPY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 October 2020, pp. 553-590
- Print publication:
- September 2022
-
- Article
- Export citation
A NEW ARGUMENT FOR KOLOMOGOROV CONDITIONALIZATION
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 930-945
- Print publication:
- December 2021
-
- Article
- Export citation
NOTE ON FOURIER–STIELTJES COEFFICIENTS OF COIN-TOSSING MEASURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 20 April 2020, pp. 479-489
- Print publication:
- December 2020
-
- Article
- Export citation
FORMAL QUALITATIVE PROBABILITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 882-909
- Print publication:
- December 2021
-
- Article
- Export citation
Orlicz Addition for Measures and an Optimization Problem for the
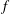 $f$-divergence
$f$-divergence
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 16 July 2019, pp. 455-479
- Print publication:
- April 2020
-
- Article
- Export citation
Reconciliation of probability measures
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 1300-1310
-
- Article
- Export citation
Influence in product spaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 145-152
- Print publication:
- July 2016
-
- Article
- Export citation
An Alternative Condition for Stochastic Domination
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1198-1200
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
On matrix exponential distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 271-292
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
The characterisation of scoring functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 135-147
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
An invariant-sum characterization of Benford's law
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 288-291
- Print publication:
- March 1997
-
- Article
- Export citation
Probabilistic convergence spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 400-420
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation