The ergodic decomposition theorem is a cornerstone result of dynamical systems and ergodic theory. It states that every invariant measure on a dynamical system is a mixture of ergodic ones. Here, we formulate and prove the theorem in terms of string diagrams, using the formalism of Markov categories. We recover the usual measure-theoretic statement by instantiating our result in the category of stochastic kernels. Along the way, we give a conceptual treatment of several concepts in the theory of deterministic and stochastic dynamical systems. In particular, ergodic measures appear very naturally as particular cones of deterministic morphisms (in the sense of Markov categories), and the invariant 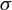$\sigma $-algebra of a dynamical system can be seen as a colimit in the category of Markov kernels. In line with other uses of category theory, once the necessary structures are in place, our proof of the main theorem is much more intuitive than traditional approaches. In particular, it does not use any quantitative limiting arguments, and it does not rely on the cardinality of the group or monoid indexing the dynamics. We hope that this result paves the way for further applications of category theory to dynamical systems, ergodic theory, and information theory.