To study when a paratopological group becomes a topological group, Arhangel’skii et al. [‘Topological games and topologies on groups’, Math. Maced. 8 (2010), 1–19] introduced the class of 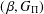 $(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourable spaces. We show that every
$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourable spaces. We show that every 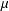 $\unicode[STIX]{x1D707}$-complete (or normal)
$\unicode[STIX]{x1D707}$-complete (or normal) 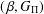 $(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourable semitopological group is a topological group. We prove that the product of a
$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourable semitopological group is a topological group. We prove that the product of a 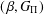 $(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourable space and a strongly Fréchet
$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourable space and a strongly Fréchet 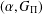 $(\unicode[STIX]{x1D6FC},G_{\unicode[STIX]{x1D6F1}})$-favourable space is
$(\unicode[STIX]{x1D6FC},G_{\unicode[STIX]{x1D6F1}})$-favourable space is 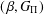 $(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourable. We also show that continuous closed irreducible mappings preserve the
$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourable. We also show that continuous closed irreducible mappings preserve the 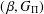 $(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourableness in both directions.
$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourableness in both directions.
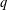 $q$-CONGRUENCES
$q$-CONGRUENCES
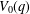 $V_{0}(q)$
$V_{0}(q)$
 $m$-FIBONACCI PARTITIONS
$m$-FIBONACCI PARTITIONS
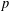 $p$-SUBGROUPS
$p$-SUBGROUPS
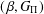 $(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-UNFAVOURABLE SPACES
$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-UNFAVOURABLE SPACES