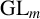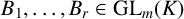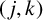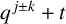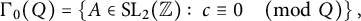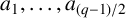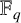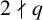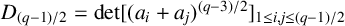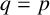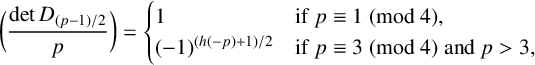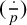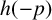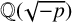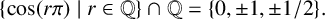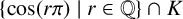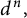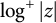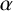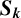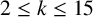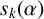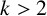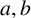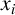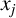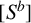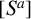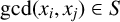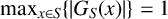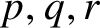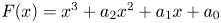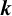41 results in 11Cxx
A MORDELL–LANG-TYPE PROBLEM FOR
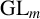 $\mathrm{GL}_{m}$
$\mathrm{GL}_{m}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
A new formula for the determinant and bounds on its tensor and Waring ranks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTERISTIC POLYNOMIALS OF THE MATRICES WITH
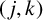 $(\,j,k)$-ENTRY
$(\,j,k)$-ENTRY 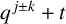 $q^{\,j\pm k}+t$
$q^{\,j\pm k}+t$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
Counting elements of the congruence subgroup
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1-15
-
- Article
-
- You have access
- HTML
- Export citation
ON MATRICES ARISING IN FINITE FIELD HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-6
-
- Article
-
- You have access
- HTML
- Export citation
ON GENERALISED LEGENDRE MATRICES INVOLVING ROOTS OF UNITY OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 199-210
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
Representatives of similarity classes of matrices over PIDs corresponding to ideal classes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 88-103
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME COUNTING QUESTIONS FOR MATRIX PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 32-43
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
A DYNAMICAL SYSTEM PROOF OF NIVEN’S THEOREM AND ITS EXTENSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 June 2023, pp. 138-151
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
LEFT AND RIGHT EIGENVECTORS OF A VARIANT OF THE SYLVESTER–KAC MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 19 June 2023, pp. 316-326
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mahler measure of polynomial iterates
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 881-885
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ANALOGUE OF THE SCHUR–SIEGEL–SMYTH TRACE PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 August 2022, pp. 227-238
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
THE ABSOLUTE
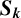 $\boldsymbol {S_k}$
-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
$\boldsymbol {S_k}$
-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 11 August 2022, pp. 239-249
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
ON THE DIVISIBILITY AMONG POWER LCM MATRICES ON GCD-CLOSED SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 19 May 2022, pp. 31-39
- Print publication:
- February 2023
-
- Article
-
- You have access
- HTML
- Export citation
Combinatorial and harmonic-analytic methods for integer tilings
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 March 2022, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On monic abelian cubics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 16 May 2022, pp. 550-567
- Print publication:
- March 2022
-
- Article
- Export citation
APPLICATIONS OF CIRCULANT MATRICES TO DETERMINANTS INVOLVING
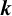 $\boldsymbol {k}$
TH POWER RESIDUES
$\boldsymbol {k}$
TH POWER RESIDUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 09 February 2022, pp. 243-253
- Print publication:
- October 2022
-
- Article
- Export citation
AN EFFECTIVE ANALYTIC FORMULA FOR THE NUMBER OF DISTINCT IRREDUCIBLE FACTORS OF A POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 339-356
- Print publication:
- December 2022
-
- Article
- Export citation
A NOTE ON GIRSTMAIR’S IRREDUCIBILITY CRITERION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 04 November 2021, pp. 62-66
- Print publication:
- August 2022
-
- Article
- Export citation
HANKEL DETERMINANTS OF FACTORIAL FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 June 2021, pp. 46-57
- Print publication:
- February 2022
-
- Article
- Export citation