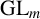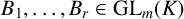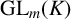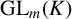1. Introduction
Many important classes of Diophantine problems can be formulated by starting with a set of invertible matrices
![]() $B_1,\ldots ,B_r\in \mathrm {GL}_m$
(over some algebraically closed field K) and studying the set
$B_1,\ldots ,B_r\in \mathrm {GL}_m$
(over some algebraically closed field K) and studying the set
for a given subvariety
![]() $V\subseteq \mathrm {GL}_m(K)$
. We mention just a small sample of questions that fall under this framework. When
$V\subseteq \mathrm {GL}_m(K)$
. We mention just a small sample of questions that fall under this framework. When
![]() $r=1$
,
$r=1$
,
![]() $K=\mathbb {Q}$
and V is the set of matrices whose
$K=\mathbb {Q}$
and V is the set of matrices whose
![]() $(1,1)$
-entry is zero then this question is equivalent to Skolem’s problem, which asks whether there is a decision procedure to determine if an integer linear recurrence has a zero. By increasing r and using block diagonal matrices, we can similarly study solutions
$(1,1)$
-entry is zero then this question is equivalent to Skolem’s problem, which asks whether there is a decision procedure to determine if an integer linear recurrence has a zero. By increasing r and using block diagonal matrices, we can similarly study solutions
![]() $(n_1,\ldots ,n_r)\in \mathbb {N}^r$
to
$(n_1,\ldots ,n_r)\in \mathbb {N}^r$
to
![]() $f_1(n_1)+\cdots +f_r(n_r)=0$
, where
$f_1(n_1)+\cdots +f_r(n_r)=0$
, where
![]() $f_1,\ldots ,f_r$
are sequences satisfying linear recurrences. This problem was considered by Cerlienco et al. [Reference Cerlienco, Mignotte and Piras2] and it was later shown by Derksen and Masser [Reference Derksen and Masser3] that determining whether there is a solution is undecidable.
$f_1,\ldots ,f_r$
are sequences satisfying linear recurrences. This problem was considered by Cerlienco et al. [Reference Cerlienco, Mignotte and Piras2] and it was later shown by Derksen and Masser [Reference Derksen and Masser3] that determining whether there is a solution is undecidable.
The above construction can be further generalised by considering some ambient algebraic variety G endowed with finitely many self-maps
![]() $\varphi _1,\dots , \varphi _r$
, and a given starting point
$\varphi _1,\dots , \varphi _r$
, and a given starting point
![]() $\alpha \in G$
and a subvariety
$\alpha \in G$
and a subvariety
![]() $V\subset G$
. Then one studies the structure of the set
$V\subset G$
. Then one studies the structure of the set
The Mordell–Lang conjecture (proven by Laurent [Reference Laurent8] in the case of algebraic tori, by Faltings [Reference Faltings, Cristante and Messing4] in the case of abelian varieties and by Vojta [Reference Vojta12] for arbitrary semiabelian varieties) asserts that if G is a semiabelian variety (defined over an algebraically closed field K of characteristic
![]() $0$
), then the intersection of any finitely generated subgroup
$0$
), then the intersection of any finitely generated subgroup
![]() $\Gamma $
of
$\Gamma $
of
![]() $G(K)$
with a subvariety
$G(K)$
with a subvariety
![]() $V\subset G$
is a finite union of cosets of subgroups of
$V\subset G$
is a finite union of cosets of subgroups of
![]() $\Gamma $
. This famed conjecture can easily be translated into a question of type (1.2) by taking the self-maps
$\Gamma $
. This famed conjecture can easily be translated into a question of type (1.2) by taking the self-maps
![]() $\varphi _i$
on G to be translations by elements from a finite set of generators for
$\varphi _i$
on G to be translations by elements from a finite set of generators for
![]() $\Gamma $
. This alternative interpretation of the classical Mordell–Lang question led to the formulation of the dynamical Mordell–Lang conjecture. (See [Reference Bell, Ghioca and Tucker1] for a comprehensive treatment of this problem.)
$\Gamma $
. This alternative interpretation of the classical Mordell–Lang question led to the formulation of the dynamical Mordell–Lang conjecture. (See [Reference Bell, Ghioca and Tucker1] for a comprehensive treatment of this problem.)
Recently, two of the authors (see [Reference Huang7] and Ghioca and Huang, ‘A non-abelian variant of the classical Mordell–Lang conjecture’, submitted for publication) have investigated S-unit equations in finite-dimensional division rings. By embedding these rings into matrix rings, one can phrase many of these ‘noncommutative S-unit questions’ in the above general framework.
As it turns out, there is a natural dichotomy that arises when studying the original problem (1.1) inside
![]() $\mathrm {GL}_m$
. When the matrices are diagonalisable, then the solution sets are well behaved and a version of the Mordell–Lang conjecture holds in this context (see [Reference Ghioca, Tucker and Zieve6, Theorem 1.3]). Even though the result from [Reference Ghioca, Tucker and Zieve6] is stated in the context of endomorphisms of semiabelian varieties, the problem translates immediately to a question regarding finitely generated subgroups of
$\mathrm {GL}_m$
. When the matrices are diagonalisable, then the solution sets are well behaved and a version of the Mordell–Lang conjecture holds in this context (see [Reference Ghioca, Tucker and Zieve6, Theorem 1.3]). Even though the result from [Reference Ghioca, Tucker and Zieve6] is stated in the context of endomorphisms of semiabelian varieties, the problem translates immediately to a question regarding finitely generated subgroups of
![]() $\mathrm {GL}_m$
of diagonalisable matrices. Indeed, given diagonalisable matrices
$\mathrm {GL}_m$
of diagonalisable matrices. Indeed, given diagonalisable matrices
![]() $B_i$
, that is,
$B_i$
, that is,
then the question of finding all r-tuples
![]() $(n_1,\dots , n_r)\in {\mathbb Z}^r$
with the property that
$(n_1,\dots , n_r)\in {\mathbb Z}^r$
with the property that
reduces to the classical Mordell–Lang problem for algebraic tori, solved by Laurent [Reference Laurent8]. However, when one allows arbitrary matrices
![]() $B_i$
, the above general question becomes undecidable and work of Scanlon and Yasufuku [Reference Scanlon and Yasufuku10] shows that any Diophantine subset of
$B_i$
, the above general question becomes undecidable and work of Scanlon and Yasufuku [Reference Scanlon and Yasufuku10] shows that any Diophantine subset of
![]() $\mathbb {N}^r$
can be realised as the set of solutions to an equation
$\mathbb {N}^r$
can be realised as the set of solutions to an equation
![]() $B_1^{n_1}\cdots B_r^{n_r}\in V$
for a subvariety V of
$B_1^{n_1}\cdots B_r^{n_r}\in V$
for a subvariety V of
![]() $\mathrm {GL}_m(K)$
. The fundamental difference between these two situations is that in the diagonalisable case, the analysis reduces to the study of equations
$\mathrm {GL}_m(K)$
. The fundamental difference between these two situations is that in the diagonalisable case, the analysis reduces to the study of equations
(with P a polynomial and
![]() $\lambda _{i,j}$
eigenvalues of the matrices), which, although difficult, can be greatly aided with the help of theorems on S-unit equations (see [Reference Laurent8, Reference Schlickewei11]).
$\lambda _{i,j}$
eigenvalues of the matrices), which, although difficult, can be greatly aided with the help of theorems on S-unit equations (see [Reference Laurent8, Reference Schlickewei11]).
In the nondiagnonalisable case, however, one must now contend with polynomial- exponential equations and the famed DPRM theorem (see [Reference Matiyasevich9]) shows that every recursively enumerable subset of
![]() $\mathbb {N}^r$
(that is, every subset that can be enumerated by a Turing machine) can be realised as the zero set of such an equation.
$\mathbb {N}^r$
(that is, every subset that can be enumerated by a Turing machine) can be realised as the zero set of such an equation.
Somewhat surprisingly, we are able to show that the pathologies that arise in the nondiagonalisable case can be handled when one imposes conditions on the eigenvalues of the matrix generators and only considers subvarieties V of
![]() $M_n(K)$
that do not pass through the origin. Given a field K, we recall that a collection of elements
$M_n(K)$
that do not pass through the origin. Given a field K, we recall that a collection of elements
![]() $s_1,\dots ,s_r\in \overline {K}^\times $
is multiplicatively independent if
$s_1,\dots ,s_r\in \overline {K}^\times $
is multiplicatively independent if
![]() $n_1,\dots ,n_r\in {\mathbb Z}$
and
$n_1,\dots ,n_r\in {\mathbb Z}$
and
![]() $s_1^{n_1} \cdots s_r^{n_r}=1$
imply that
$s_1^{n_1} \cdots s_r^{n_r}=1$
imply that
![]() $n_1=\cdots =n_r=0$
. We say a collection of elements
$n_1=\cdots =n_r=0$
. We say a collection of elements
![]() $B_1,\dots ,B_r\in M_r(K)$
has multiplicatively independent eigenvalues if the set of eigenvalues (counted without multiplicity) of
$B_1,\dots ,B_r\in M_r(K)$
has multiplicatively independent eigenvalues if the set of eigenvalues (counted without multiplicity) of
![]() $B_1,\ldots ,B_r$
are pairwise disjoint and their union is multiplicatively independent. Our main result is the following general Mordell–Lang variant.
$B_1,\ldots ,B_r$
are pairwise disjoint and their union is multiplicatively independent. Our main result is the following general Mordell–Lang variant.
Theorem 1.1. Let K be an algebraically closed field of characteristic zero, let
![]() $B_1,\dots ,B_r\in \mathrm {GL}_m(K)$
be matrices with multiplicatively independent eigenvalues and let V be a closed subvariety of
$B_1,\dots ,B_r\in \mathrm {GL}_m(K)$
be matrices with multiplicatively independent eigenvalues and let V be a closed subvariety of
![]() $\mathrm {GL}_m(K)$
not passing through zero. If
$\mathrm {GL}_m(K)$
not passing through zero. If
then
![]() $\lvert {V(K)\cap \Gamma \rvert } < \infty $
.
$\lvert {V(K)\cap \Gamma \rvert } < \infty $
.
In fact, we prove a slightly more general (although equivalent) version of Theorem 1.1 for central simple algebras (see Theorem 2.2), which has the advantage of being immediately applicable to recent ‘noncommutative’ variants of the Mordell–Lang problem.
We note that the finiteness we obtain can be viewed as the ‘generic’ situation of the Mordell–Lang conjecture; that is, one generally expects the intersection of a finitely generated group in a semiabelian variety with a subvariety to be finite unless there is some additional geometric structure that explains the infinite intersection. One cannot expect to get a general finiteness result of the form given in Theorem 2.2 without some mild constraints. We give examples in Section 2.3 which show that attempts to weaken the hypotheses can give rise to pathological intersection sets.
The outline of this paper is as follows. In Section 2, we state a couple of technical results, which are both variants of the classical Mordell–Lang problem in two different settings. Theorem 2.2 is an equivalent formulation of Theorem 1.1 in the context of finite-dimensional central simple algebras, while Theorem 2.7 is a variant of the classical Mordell–Lang theorem in the context of commutative linear algebraic groups. Theorem 2.7 is also a key ingredient in our proof of Theorem 2.2. We prove Theorem 2.7 in Section 3 and we conclude our proof of Theorem 2.2 in Section 4.
2. A couple of variants of the classical Mordell–Lang conjecture
We start by setting the notation for our paper.
2.1. Notation
Throughout this paper, let
![]() ${\mathbb N}$
denote the set of nonnegative integers, K be a field of characteristic
${\mathbb N}$
denote the set of nonnegative integers, K be a field of characteristic
![]() $0$
and A be a finite-dimensional central simple algebra over K. We let
$0$
and A be a finite-dimensional central simple algebra over K. We let
![]() $\ell :=[A:K]$
. Geometrically, A can be identified with the K-points of the
$\ell :=[A:K]$
. Geometrically, A can be identified with the K-points of the
![]() $\ell $
-dimensional affine space
$\ell $
-dimensional affine space
![]() $\mathbb {A}^\ell (K)$
. Moreover, since the multiplicative group
$\mathbb {A}^\ell (K)$
. Moreover, since the multiplicative group
![]() $A^\times $
embeds into
$A^\times $
embeds into
![]() $\operatorname {\mathrm {GL}}_\ell (K)$
by
$\operatorname {\mathrm {GL}}_\ell (K)$
by
![]() $f\mapsto L_f$
, where
$f\mapsto L_f$
, where
![]() $L_f:A\to A$
is the left-multiplication map by f, we see that
$L_f:A\to A$
is the left-multiplication map by f, we see that
![]() $A^\times $
can be identified with the K-points of a linear algebraic group. For
$A^\times $
can be identified with the K-points of a linear algebraic group. For
![]() $f\in A$
, we define
$f\in A$
, we define
![]() $\Lambda _f$
to be the set of eigenvalues of
$\Lambda _f$
to be the set of eigenvalues of
![]() $L_f$
over the algebraic closure
$L_f$
over the algebraic closure
![]() $\overline {K}$
, not counting multiplicities.
$\overline {K}$
, not counting multiplicities.
Definition 2.1. We say a collection of elements
![]() $f_1,\dots ,f_r\in A^\times $
has multiplicatively independent eigenvalues if
$f_1,\dots ,f_r\in A^\times $
has multiplicatively independent eigenvalues if
![]() $\Lambda _{f_1},\dots ,\Lambda _{f_r}$
are disjoint and their union is multiplicatively independent.
$\Lambda _{f_1},\dots ,\Lambda _{f_r}$
are disjoint and their union is multiplicatively independent.
In this paper, unless otherwise noted, each algebraic group is connected.
2.2. A variant of the Mordell–Lang problem for central simple algebras
The following result is an equivalent re-statement of Theorem 1.1 in the setting of finite-dimensional central simple algebras.
Theorem 2.2. Let
![]() $K,A$
be as above, V be a closed K-subvariety of A not passing through zero,
$K,A$
be as above, V be a closed K-subvariety of A not passing through zero,
![]() $f_1,\dots ,f_r\in A^\times $
, and
$f_1,\dots ,f_r\in A^\times $
, and
![]() $\Gamma $
be the set
$\Gamma $
be the set
If
![]() $f_1,\dots , f_r$
have multiplicatively independent eigenvalues, then
$f_1,\dots , f_r$
have multiplicatively independent eigenvalues, then
![]() $\lvert {V(K)\cap \Gamma \rvert } < \infty $
.
$\lvert {V(K)\cap \Gamma \rvert } < \infty $
.
Next, we present various examples showing the relevance of the hypotheses from Theorem 2.2.
2.3. Examples
We first recall that for any nilpotent matrix x in
![]() $\operatorname {\mathrm {Mat}}_n(K)$
(so that
$\operatorname {\mathrm {Mat}}_n(K)$
(so that
![]() $x^n=0$
), there is a well-defined unipotent matrix
$x^n=0$
), there is a well-defined unipotent matrix
 $$ \begin{align*} \exp(x):=\sum_{k=0}^\infty \frac{x^k}{k!} = \sum_{k=0}^{n-1} \frac{x^k}{k!}. \end{align*} $$
$$ \begin{align*} \exp(x):=\sum_{k=0}^\infty \frac{x^k}{k!} = \sum_{k=0}^{n-1} \frac{x^k}{k!}. \end{align*} $$
Moreover,
![]() $\exp (x+y)=\exp (x)\exp (y)$
if
$\exp (x+y)=\exp (x)\exp (y)$
if
![]() $xy=yx$
.
$xy=yx$
.
We denote by
![]() $\varepsilon _n$
the nilpotent matrix
$\varepsilon _n$
the nilpotent matrix
 $$ \begin{align*} \varepsilon_n:=\begin{bmatrix} 0 & 1 & & \\ & 0 & \ddots & \\ & & \ddots & 1 \\ & & & 0 \end{bmatrix} \in \operatorname{\mathrm{Mat}}_n(K). \end{align*} $$
$$ \begin{align*} \varepsilon_n:=\begin{bmatrix} 0 & 1 & & \\ & 0 & \ddots & \\ & & \ddots & 1 \\ & & & 0 \end{bmatrix} \in \operatorname{\mathrm{Mat}}_n(K). \end{align*} $$
The following example shows the necessity of the assumption of Theorem 2.2 that V does not pass through
![]() $0$
.
$0$
.
Example 2.3. Let
![]() $A=\operatorname {\mathrm {Mat}}_3(K)$
,
$A=\operatorname {\mathrm {Mat}}_3(K)$
,
![]() $\varepsilon :=\varepsilon _3$
,
$\varepsilon :=\varepsilon _3$
,
![]() $f_1=2\exp (\varepsilon )$
and
$f_1=2\exp (\varepsilon )$
and
![]() $f_2=3\exp (-\varepsilon ^2)$
. Then for
$f_2=3\exp (-\varepsilon ^2)$
. Then for
![]() $n_1,n_2\in {\mathbb Z}$
,
$n_1,n_2\in {\mathbb Z}$
,
 $$ \begin{align*} f_1^{n_1}f_2^{n_2}=2^{n_1}3^{n_2}\exp(n_1 \varepsilon-n_2 \varepsilon^2) = 2^{n_1} 3^{n_2} \bigg(1+n_1 \varepsilon + \bigg(-n_2+\frac{n_1^2}{2}\bigg) \varepsilon^2\bigg). \end{align*} $$
$$ \begin{align*} f_1^{n_1}f_2^{n_2}=2^{n_1}3^{n_2}\exp(n_1 \varepsilon-n_2 \varepsilon^2) = 2^{n_1} 3^{n_2} \bigg(1+n_1 \varepsilon + \bigg(-n_2+\frac{n_1^2}{2}\bigg) \varepsilon^2\bigg). \end{align*} $$
Hence, if
![]() $V\subseteq A$
is cut out by the condition that the top-right entry is zero, then
$V\subseteq A$
is cut out by the condition that the top-right entry is zero, then
![]() $f_1^{n_1} f_2^{n_2}\in V$
if and only if
$f_1^{n_1} f_2^{n_2}\in V$
if and only if
![]() $n_2={n_1^2}/{2}$
. The corresponding subset in
$n_2={n_1^2}/{2}$
. The corresponding subset in
![]() ${\mathbb Z}^2$
is not only infinite, but also not a finite union of cosets of subgroups of
${\mathbb Z}^2$
is not only infinite, but also not a finite union of cosets of subgroups of
![]() ${\mathbb Z}^2$
.
${\mathbb Z}^2$
.
In this example,
![]() $f_1,f_2$
have multiplicatively independent eigenvalues, but
$f_1,f_2$
have multiplicatively independent eigenvalues, but
![]() $0\in V$
.
$0\in V$
.
In view of Ghioca and Huang (‘A non-abelian variant of the classical Mordell–Lang conjecture’, submitted for publication), it is tempting to replace the assumption of Theorem 2.2 that
![]() $f_1,\dots ,f_r$
have multiplicatively independent eigenvalues by the assumption that
$f_1,\dots ,f_r$
have multiplicatively independent eigenvalues by the assumption that
![]() $\det (f_1)$
,
$\det (f_1)$
,
![]() $\dots ,\det (f_r)$
are multiplicatively independent. The following example shows we cannot do so.
$\dots ,\det (f_r)$
are multiplicatively independent. The following example shows we cannot do so.
Example 2.4. Let
![]() $A=\operatorname {\mathrm {Mat}}_4(K)$
,
$A=\operatorname {\mathrm {Mat}}_4(K)$
,
![]() $\varepsilon :=\varepsilon _3$
,
$\varepsilon :=\varepsilon _3$
,
![]() $f_1=\mathrm {diag}(2\exp (\varepsilon ),1)\in \operatorname {\mathrm {Mat}}_{3+1}(K)$
and
$f_1=\mathrm {diag}(2\exp (\varepsilon ),1)\in \operatorname {\mathrm {Mat}}_{3+1}(K)$
and
![]() $f_2=\mathrm {diag}(3\exp (-\varepsilon ^2),1)$
. Let
$f_2=\mathrm {diag}(3\exp (-\varepsilon ^2),1)$
. Let
![]() $V\subseteq A$
be cut out by the condition that the
$V\subseteq A$
be cut out by the condition that the
![]() $(3,1)$
-entry is zero and the
$(3,1)$
-entry is zero and the
![]() $(4,4)$
-entry is
$(4,4)$
-entry is
![]() $1$
. Then by the same argument as the preceding example,
$1$
. Then by the same argument as the preceding example,
![]() $f_1^{n_1}f_2^{n_2}\in V$
if and only if
$f_1^{n_1}f_2^{n_2}\in V$
if and only if
![]() $n_2={n_1^2}/{2}$
.
$n_2={n_1^2}/{2}$
.
In this example,
![]() $0\notin V$
, and
$0\notin V$
, and
![]() $\det (f_1)=2^3, \det (f_2)=3^3$
are multiplicatively independent. However,
$\det (f_1)=2^3, \det (f_2)=3^3$
are multiplicatively independent. However,
![]() $f_1$
has eigenvalues
$f_1$
has eigenvalues
![]() $\{2,1\}$
, and the presence of
$\{2,1\}$
, and the presence of
![]() $1$
implies that
$1$
implies that
![]() $f_1,f_2$
do not have multiplicatively independent eigenvalues.
$f_1,f_2$
do not have multiplicatively independent eigenvalues.
Finally, the next example shows that if one were to replace the set
![]() $\Gamma $
from Theorem 2.2 with the subgroup generated by
$\Gamma $
from Theorem 2.2 with the subgroup generated by
![]() $f_1,\dots , f_r$
, then the conclusion would fail.
$f_1,\dots , f_r$
, then the conclusion would fail.
Example 2.5. Let
![]() $A=\operatorname {\mathrm {Mat}}_2(K)$
,
$A=\operatorname {\mathrm {Mat}}_2(K)$
,
![]() $f_1=\mathrm {diag}(2,3)$
and
$f_1=\mathrm {diag}(2,3)$
and
![]() $f_2=\mathrm {diag}(5,7)+\varepsilon $
, where
$f_2=\mathrm {diag}(5,7)+\varepsilon $
, where
![]() $\varepsilon =\big [\begin {smallmatrix} 0 & 1 \\ 0 & 0 \end {smallmatrix}\big ]$
. Then the subgroup
$\varepsilon =\big [\begin {smallmatrix} 0 & 1 \\ 0 & 0 \end {smallmatrix}\big ]$
. Then the subgroup
![]() $\Gamma $
generated by
$\Gamma $
generated by
![]() $f_1, f_2$
contains
$f_1, f_2$
contains
![]() $u:=f_1 f_2 f_1^{-1} f_2^{-1}=I_2 - \varepsilon /21$
. In particular,
$u:=f_1 f_2 f_1^{-1} f_2^{-1}=I_2 - \varepsilon /21$
. In particular,
![]() $u^n$
for
$u^n$
for
![]() $n\in {\mathbb N}$
gives infinitely many elements in
$n\in {\mathbb N}$
gives infinitely many elements in
![]() $V(K)\cap \Gamma $
, where
$V(K)\cap \Gamma $
, where
 $$ \begin{align*} V=\left\{{\begin{bmatrix} a & b\\c & d \end{bmatrix}: a=d=1, c=0}\right\}. \end{align*} $$
$$ \begin{align*} V=\left\{{\begin{bmatrix} a & b\\c & d \end{bmatrix}: a=d=1, c=0}\right\}. \end{align*} $$
2.4. A variant of the Mordell–Lang problem in an arbitrary commutative algebraic group
Theorem 2.7 is our key ingredient for proving Theorem 2.2 and it is itself another variant of the classical Mordell–Lang problem (this time in the context of the commutative linear algebraic groups).
One of the most important special cases of the classical Mordell–Lang conjecture says that given a semiabelian variety G (defined over an algebraically closed field K of characteristic
![]() $0$
) and given a finitely generated subgroup
$0$
) and given a finitely generated subgroup
![]() $\Gamma \subset G(K)$
, if
$\Gamma \subset G(K)$
, if
then
![]() $|V(K)\cap \Gamma |<\infty $
. It is natural to consider extensions of the classical Mordell–Lang conjecture to arbitrary commutative algebraic groups G. The first such case to consider would be for affine groups, that is, when G is isomorphic to
$|V(K)\cap \Gamma |<\infty $
. It is natural to consider extensions of the classical Mordell–Lang conjecture to arbitrary commutative algebraic groups G. The first such case to consider would be for affine groups, that is, when G is isomorphic to
![]() $\mathbb {G}_m^\ell \times \mathbb {G}_a^k$
for some
$\mathbb {G}_m^\ell \times \mathbb {G}_a^k$
for some
![]() $k,\ell \in {\mathbb N}$
, and once again study this problem under the assumption (2.1). However, [Reference Ghioca, Hu, Scanlon and Zannier5, Examples 1.1 and 1.2] show that the presence of multiple copies of
$k,\ell \in {\mathbb N}$
, and once again study this problem under the assumption (2.1). However, [Reference Ghioca, Hu, Scanlon and Zannier5, Examples 1.1 and 1.2] show that the presence of multiple copies of
![]() $\mathbb {G}_a$
will generate counterexamples of the Mordell–Lang principle. Our next Theorem 2.7 provides a setting where the aforementioned variant of the Mordell–Lang conjecture holds even in the presence of arbitrarily many copies of
$\mathbb {G}_a$
will generate counterexamples of the Mordell–Lang principle. Our next Theorem 2.7 provides a setting where the aforementioned variant of the Mordell–Lang conjecture holds even in the presence of arbitrarily many copies of
![]() $\mathbb {G}_a$
in the linear algebraic group G.
$\mathbb {G}_a$
in the linear algebraic group G.
To state Theorem 2.7, we need the following definition.
Definition 2.6. Let G be a commutative linear algebraic group over a field K of characteristic
![]() $0$
, and
$0$
, and
![]() $\Gamma $
be a finitely generated subgroup of
$\Gamma $
be a finitely generated subgroup of
![]() $G(K)$
. We say
$G(K)$
. We say
![]() $\Gamma \subseteq G(K)$
is strongly independent if there are
$\Gamma \subseteq G(K)$
is strongly independent if there are
![]() $r,\,u,\,\ell _1,\dots ,\ell _r\in {\mathbb Z}_{\geq 0}$
and an isomorphism
$r,\,u,\,\ell _1,\dots ,\ell _r\in {\mathbb Z}_{\geq 0}$
and an isomorphism
![]() $G\simeq \mathbb {G}_m^{\ell _1+\cdots +\ell _r}\times \mathbb {G}_a^u$
, under which a generating set
$G\simeq \mathbb {G}_m^{\ell _1+\cdots +\ell _r}\times \mathbb {G}_a^u$
, under which a generating set
![]() $g_1,\dots ,g_r$
of
$g_1,\dots ,g_r$
of
![]() $\Gamma $
takes the form
$\Gamma $
takes the form
 $$ \begin{align} \begin{aligned} g_1 &= (\lambda_{1,1},\dots,\lambda_{1,\ell_1})\times (1,\dots,1) \times \cdots \times (1,\dots,1) \times \overline{b}_1,\\ g_2 &= (1,\dots,1) \times (\lambda_{2,1},\dots,\lambda_{2,\ell_2}) \times \cdots \times (1,\dots,1) \times \overline{b}_2, \\ &\vdots \\ g_r &= (1,\dots,1) \times (1,\dots,1) \times \cdots \times (\lambda_{r,1},\dots,\lambda_{r,\ell_r}) \times \overline{b}_r, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} g_1 &= (\lambda_{1,1},\dots,\lambda_{1,\ell_1})\times (1,\dots,1) \times \cdots \times (1,\dots,1) \times \overline{b}_1,\\ g_2 &= (1,\dots,1) \times (\lambda_{2,1},\dots,\lambda_{2,\ell_2}) \times \cdots \times (1,\dots,1) \times \overline{b}_2, \\ &\vdots \\ g_r &= (1,\dots,1) \times (1,\dots,1) \times \cdots \times (\lambda_{r,1},\dots,\lambda_{r,\ell_r}) \times \overline{b}_r, \end{aligned} \end{align} $$
where
![]() $\lambda _{i,j}\in K^\times $
are multiplicatively independent and
$\lambda _{i,j}\in K^\times $
are multiplicatively independent and
![]() $\overline {b}_1,\dots ,\overline {b}_r\in K^u$
(that is, they are K-vectors with u entries). In this case, we let
$\overline {b}_1,\dots ,\overline {b}_r\in K^u$
(that is, they are K-vectors with u entries). In this case, we let
![]() $T_i:=\mathbb {G}_m^{\ell _i}$
and
$T_i:=\mathbb {G}_m^{\ell _i}$
and
![]() $U=\mathbb {G}_a^u$
, and we say
$U=\mathbb {G}_a^u$
, and we say
![]() $\Gamma \subseteq G(K)$
is strongly independent with respect to the decomposition
$\Gamma \subseteq G(K)$
is strongly independent with respect to the decomposition
![]() $G=T_1\times \dots \times T_r\times U$
.
$G=T_1\times \dots \times T_r\times U$
.
Theorem 2.7. Let G be a commutative linear algebraic group over a field K of characteristic zero,
![]() $V\subseteq G$
be a closed subvariety and
$V\subseteq G$
be a closed subvariety and
![]() $\Gamma $
be a finitely generated subgroup of
$\Gamma $
be a finitely generated subgroup of
![]() $G(K)$
. Assume:
$G(K)$
. Assume:
-
(i) The subgroup
 $\Gamma $
is strongly independent in
$\Gamma $
is strongly independent in
 $G(K)$
with respect to some decomposition
$G(K)$
with respect to some decomposition
 $G=T_1\times \dots \times T_r\times U$
; and
$G=T_1\times \dots \times T_r\times U$
; and -
(ii) there is no
 $i\in \{1,\dots , r\}$
and no geometric point
$i\in \{1,\dots , r\}$
and no geometric point
 $v\in (\prod _{j\ne i} T_j)\times U$
such that (2.3)
$v\in (\prod _{j\ne i} T_j)\times U$
such that (2.3) $$ \begin{align} T_i\times \{{v}\} \subseteq V. \end{align} $$
$$ \begin{align} T_i\times \{{v}\} \subseteq V. \end{align} $$
Then
![]() $\lvert {V(K)\cap \Gamma \rvert } < \infty $
.
$\lvert {V(K)\cap \Gamma \rvert } < \infty $
.
2.5. Remarks regarding Theorem 2.7
We show next that the conclusion in Theorem 2.7 fails if one removes the hypotheses regarding V and
![]() $\Gamma $
.
$\Gamma $
.
First of all, condition (2.3) is a weaker version of condition (2.1) and in its absence, Theorem 2.7 would fail as the next example shows.
Example 2.8. Consider
![]() $G=\mathbb {G}_m^2$
and let
$G=\mathbb {G}_m^2$
and let
![]() $\Gamma $
be generated by
$\Gamma $
be generated by
![]() $(2,1)$
and
$(2,1)$
and
![]() $(1,3)$
, while
$(1,3)$
, while
![]() $V=\{2\}\times \mathbb {G}_m$
. Then clearly,
$V=\{2\}\times \mathbb {G}_m$
. Then clearly,
![]() $V\cap \Gamma $
is infinite. Note that in this example,
$V\cap \Gamma $
is infinite. Note that in this example,
![]() $\Gamma $
is strongly independent, but V does not satisfy hypothesis (2.3) from Theorem 2.7.
$\Gamma $
is strongly independent, but V does not satisfy hypothesis (2.3) from Theorem 2.7.
The relevance of the hypothesis that
![]() $\Gamma $
is strongly independent is more subtle. On one hand, the next example shows that in its absence, one would definitely have to strengthen the hypothesis (2.3) to the original hypothesis (2.1) from the classical Mordell–Lang problem.
$\Gamma $
is strongly independent is more subtle. On one hand, the next example shows that in its absence, one would definitely have to strengthen the hypothesis (2.3) to the original hypothesis (2.1) from the classical Mordell–Lang problem.
Example 2.9. Consider the case when
![]() $G=\mathbb {G}_m^2$
and
$G=\mathbb {G}_m^2$
and
![]() $\Gamma \subset G(K)$
is spanned by
$\Gamma \subset G(K)$
is spanned by
![]() $(2,1)$
and
$(2,1)$
and
![]() $(1,4)$
. Then
$(1,4)$
. Then
![]() $\Gamma $
is contained in the subvariety V given by the equation
$\Gamma $
is contained in the subvariety V given by the equation
![]() $x_2=x_1^2$
. We note that V meets the hypothesis (2.3) from Theorem 2.7, but since
$x_2=x_1^2$
. We note that V meets the hypothesis (2.3) from Theorem 2.7, but since
![]() $\Gamma $
is not strongly independent, the intersection
$\Gamma $
is not strongly independent, the intersection
![]() $V\cap \Gamma $
is infinite in this case.
$V\cap \Gamma $
is infinite in this case.
However, the following example shows that even if we were to strengthen the hypothesis (2.3) to (2.1), one would still not obtain the desired conclusion in Theorem 2.7 in the absence of the hypothesis that
![]() $\Gamma $
is strongly independent.
$\Gamma $
is strongly independent.
Example 2.10. Consider the case when
![]() $G=\mathbb {G}_m\times \mathbb {G}_a$
, and
$G=\mathbb {G}_m\times \mathbb {G}_a$
, and
![]() $\Gamma $
is generated by
$\Gamma $
is generated by
![]() $(2,1)$
and
$(2,1)$
and
![]() $(2,0)$
. Then
$(2,0)$
. Then
![]() $\Gamma $
has infinite intersection with the diagonal subvariety
$\Gamma $
has infinite intersection with the diagonal subvariety
![]() $V\subset G$
given by the equation
$V\subset G$
given by the equation
![]() $x_1=x_2$
. Indeed,
$x_1=x_2$
. Indeed,
![]() $\Gamma $
consists of all points of the form
$\Gamma $
consists of all points of the form
and so,
![]() $V\cap \Gamma $
consists of the set
$V\cap \Gamma $
consists of the set
which is not a finite union of cosets of subgroups of
![]() $\Gamma $
. In this case, V is a curve, which is not a coset of a subgroup of
$\Gamma $
. In this case, V is a curve, which is not a coset of a subgroup of
![]() $\Gamma $
, but nevertheless, the intersection
$\Gamma $
, but nevertheless, the intersection
![]() $V\cap \Gamma $
is infinite. Note that
$V\cap \Gamma $
is infinite. Note that
![]() $\Gamma $
is not strongly independent in this example.
$\Gamma $
is not strongly independent in this example.
3. Proof of Theorem 2.7
In this section, we work with the notation and hypotheses from Theorem 2.7 to prove it.
It suffices to prove Theorem 2.7 assuming K is algebraically closed. Therefore, we may assume
![]() $G=\mathbb {G}_m^\ell \times \mathbb {G}_a^k$
for some
$G=\mathbb {G}_m^\ell \times \mathbb {G}_a^k$
for some
![]() $\ell ,k\in \mathbb {N}$
. Furthermore, we can write
$\ell ,k\in \mathbb {N}$
. Furthermore, we can write
where the group
![]() $\Gamma $
is generated by
$\Gamma $
is generated by
 $$ \begin{align} \begin{aligned} g_1 &= (\lambda_{1,1},\dots,\lambda_{1,\ell_1})\times (1,\dots,1) \times \dots \times (1,\dots,1) \times \overline{b}_1,\\ g_2 &= (1,\dots,1) \times (\lambda_{2,1},\dots,\lambda_{2,\ell_2}) \times \dots \times (1,\dots,1) \times \overline{b}_2, \\ &\vdots \\ g_r &= (1,\dots,1) \times (1,\dots,1) \times \dots \times (\lambda_{r,1},\dots,\lambda_{r,\ell_r}) \times \overline{b}_r \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} g_1 &= (\lambda_{1,1},\dots,\lambda_{1,\ell_1})\times (1,\dots,1) \times \dots \times (1,\dots,1) \times \overline{b}_1,\\ g_2 &= (1,\dots,1) \times (\lambda_{2,1},\dots,\lambda_{2,\ell_2}) \times \dots \times (1,\dots,1) \times \overline{b}_2, \\ &\vdots \\ g_r &= (1,\dots,1) \times (1,\dots,1) \times \dots \times (\lambda_{r,1},\dots,\lambda_{r,\ell_r}) \times \overline{b}_r \end{aligned} \end{align} $$
for some
![]() $\overline {b}_1,\dots , \overline {b}_r\in \mathbb {G}_a^k(K)$
; moreover, the elements
$\overline {b}_1,\dots , \overline {b}_r\in \mathbb {G}_a^k(K)$
; moreover, the elements
![]() $\lambda _{i,j}\in K^\times $
are multiplicatively independent. We write
$\lambda _{i,j}\in K^\times $
are multiplicatively independent. We write
where each
![]() $b_{i,j}\in K$
(for
$b_{i,j}\in K$
(for
![]() $1\le i\le r$
and
$1\le i\le r$
and
![]() $1\le j\le k$
).
$1\le j\le k$
).
Taking into account that
![]() $\ell =\ell _1+\cdots +\ell _r$
, we represent each polynomial f in the vanishing ideal
$\ell =\ell _1+\cdots +\ell _r$
, we represent each polynomial f in the vanishing ideal
![]() $\mathcal {I}(V)$
of V as a polynomial in
$\mathcal {I}(V)$
of V as a polynomial in
So, we let
![]() $f_1,\dots , f_m$
be a given set of generators for
$f_1,\dots , f_m$
be a given set of generators for
![]() $\mathcal {I}(V)$
and we consider next
$\mathcal {I}(V)$
and we consider next
![]() $f_s$
for some s with
$f_s$
for some s with
![]() $1\le s\le m$
. Then we can write
$1\le s\le m$
. Then we can write
![]() $f_s$
as
$f_s$
as
 $$ \begin{align} f_s:=\sum_{\overline{j}=(j_{i,u})_{\tiny\substack{{1\le i\le r}\\ 1\le u\le \ell_i}}} \prod_{i=1}^r\prod_{u=1}^{\ell_i} x_{i,u}^{j_{i,u}}\cdot P_{s,\overline{j}}(y_1,\dots, y_k), \end{align} $$
$$ \begin{align} f_s:=\sum_{\overline{j}=(j_{i,u})_{\tiny\substack{{1\le i\le r}\\ 1\le u\le \ell_i}}} \prod_{i=1}^r\prod_{u=1}^{\ell_i} x_{i,u}^{j_{i,u}}\cdot P_{s,\overline{j}}(y_1,\dots, y_k), \end{align} $$
where the sum in (3.3) runs over a finite set
![]() $J_s$
of tuples
$J_s$
of tuples
while
![]() $P_{s,\overline {j}}\in K[y_1,\dots , y_k]$
is some nonzero polynomial.
$P_{s,\overline {j}}\in K[y_1,\dots , y_k]$
is some nonzero polynomial.
For each
![]() $\overline {j}\in J_s$
, there is a polynomial
$\overline {j}\in J_s$
, there is a polynomial
![]() $Q_{s,\overline {j}}\in K[z_1,\dots , z_r]$
(depending on the
$Q_{s,\overline {j}}\in K[z_1,\dots , z_r]$
(depending on the
![]() $\overline {b}_i$
terms, according to (3.2)) with the property that
$\overline {b}_i$
terms, according to (3.2)) with the property that
 $$ \begin{align} Q_{s,\overline{j}}(n_1,\dots, n_r):=P_{s,\overline{j}}\bigg(\sum_{i=1}^r n_i\cdot \overline{b}_i\bigg) \quad\text{for each }n_1,\dots, n_r\in\mathbb{Z}. \end{align} $$
$$ \begin{align} Q_{s,\overline{j}}(n_1,\dots, n_r):=P_{s,\overline{j}}\bigg(\sum_{i=1}^r n_i\cdot \overline{b}_i\bigg) \quad\text{for each }n_1,\dots, n_r\in\mathbb{Z}. \end{align} $$
Using (3.1), (3.2) and (3.4), we see that
![]() $f_s$
vanishes at the point
$f_s$
vanishes at the point
![]() $g_1^{n_1}\cdots g_r^{n_r}\in \mathbb {G}_m^\ell \times \mathbb {G}_a^k$
(for some integers
$g_1^{n_1}\cdots g_r^{n_r}\in \mathbb {G}_m^\ell \times \mathbb {G}_a^k$
(for some integers
![]() $n_1,\dots , n_r$
) if and only if
$n_1,\dots , n_r$
) if and only if
 $$ \begin{align} \sum_{\overline{j}\in J_s} \prod_{i=1}^r\prod_{u=1}^{\ell_i} \lambda_{i,u}^{j_{i,u}\cdot n_i}\cdot Q_{s,\overline{j}}(n_1,\dots, n_r)=0. \end{align} $$
$$ \begin{align} \sum_{\overline{j}\in J_s} \prod_{i=1}^r\prod_{u=1}^{\ell_i} \lambda_{i,u}^{j_{i,u}\cdot n_i}\cdot Q_{s,\overline{j}}(n_1,\dots, n_r)=0. \end{align} $$
So,
![]() $\prod _{i=1}^r g_i^{n_i}\in V$
if and only if
$\prod _{i=1}^r g_i^{n_i}\in V$
if and only if
![]() $\overline {n}:=(n_1,\dots , n_r)$
satisfies the system of equations (3.5) for
$\overline {n}:=(n_1,\dots , n_r)$
satisfies the system of equations (3.5) for
![]() $s=1,\dots ,m$
. We argue by contradiction and assume there exists an infinite set of solutions
$s=1,\dots ,m$
. We argue by contradiction and assume there exists an infinite set of solutions
![]() $\mathcal {S}:=\{\overline {n}^{(i)}\}_{i\ge 1}$
to the above system of polynomial-exponential equations (3.5). To simplify the index notation from (3.5), we re-write that equation as
$\mathcal {S}:=\{\overline {n}^{(i)}\}_{i\ge 1}$
to the above system of polynomial-exponential equations (3.5). To simplify the index notation from (3.5), we re-write that equation as
 $$ \begin{align} \sum_{\overline{j}\in J_s} \left(\overline{\lambda}^{\overline{j}}\right)^{\overline{n}}\cdot Q_{s,\overline{j}}(\overline{n})=0, \end{align} $$
$$ \begin{align} \sum_{\overline{j}\in J_s} \left(\overline{\lambda}^{\overline{j}}\right)^{\overline{n}}\cdot Q_{s,\overline{j}}(\overline{n})=0, \end{align} $$
where
![]() $\overline {\lambda }:=(\lambda _{i,u})_{\substack {1\le i\le r\\ 1\le u\le \ell _i}}$
and
$\overline {\lambda }:=(\lambda _{i,u})_{\substack {1\le i\le r\\ 1\le u\le \ell _i}}$
and
 $$ \begin{align*}\bigg(\overline{\lambda}^{\overline{j}}\bigg)^{\overline{n}}:=\prod_{i=1}^r \prod_{u=1}^{\ell_i} \lambda_{i,u}^{j_{i,u}\cdot n_i}.\end{align*} $$
$$ \begin{align*}\bigg(\overline{\lambda}^{\overline{j}}\bigg)^{\overline{n}}:=\prod_{i=1}^r \prod_{u=1}^{\ell_i} \lambda_{i,u}^{j_{i,u}\cdot n_i}.\end{align*} $$
To analyse the system of m polynomial-exponential equations (3.5), we will apply the method from [Reference Laurent8, Section 8]. Since there are finitely many partitions for each set of indices
![]() $J_s$
, there exists a given collection of partitions
$J_s$
, there exists a given collection of partitions
where
![]() $\mathcal {P}_s$
is a partition of
$\mathcal {P}_s$
is a partition of
![]() $J_s$
for each
$J_s$
for each
![]() $s=1,\dots , m$
, which is maximally compatible (as defined in [Reference Laurent8, page 320]) for infinitely many solutions
$s=1,\dots , m$
, which is maximally compatible (as defined in [Reference Laurent8, page 320]) for infinitely many solutions
![]() $\overline {n}\in \mathcal {S}$
for the system of polynomial-exponential equations (3.5). At the expense of replacing
$\overline {n}\in \mathcal {S}$
for the system of polynomial-exponential equations (3.5). At the expense of replacing
![]() $\mathcal {S}$
by a suitable infinite subset, we may assume that each of the solutions
$\mathcal {S}$
by a suitable infinite subset, we may assume that each of the solutions
![]() $\overline {n}\in \mathcal {S}$
is maximally compatible with the given partition (3.7). The compatibility of the collection of partitions
$\overline {n}\in \mathcal {S}$
is maximally compatible with the given partition (3.7). The compatibility of the collection of partitions
![]() $\mathcal {P}$
with respect to each solution
$\mathcal {P}$
with respect to each solution
![]() $\overline {n}\in \mathcal {S}$
refers to the fact that for each
$\overline {n}\in \mathcal {S}$
refers to the fact that for each
![]() $s=1,\dots , m$
, considering the partition
$s=1,\dots , m$
, considering the partition
![]() $\mathcal {P}_s$
of
$\mathcal {P}_s$
of
![]() $J_s$
given by
$J_s$
given by
we have, for each
![]() $s=1,\dots , m$
,
$s=1,\dots , m$
,
 $$ \begin{align} \sum_{\overline{j}\in J_{s,i}} \bigg(\overline{\lambda}^{\overline{j}}\bigg)^{\overline{n}} Q_{s,\overline{j}}(\overline{n})=0 \quad\text{for each }i=1,\dots,v_s. \end{align} $$
$$ \begin{align} \sum_{\overline{j}\in J_{s,i}} \bigg(\overline{\lambda}^{\overline{j}}\bigg)^{\overline{n}} Q_{s,\overline{j}}(\overline{n})=0 \quad\text{for each }i=1,\dots,v_s. \end{align} $$
The maximality of the collection
![]() $\mathcal {P}$
refers to the fact that there is no further refined collection of partitions (3.8) such that equations (3.9) hold for each subpart of each corresponding partition of
$\mathcal {P}$
refers to the fact that there is no further refined collection of partitions (3.8) such that equations (3.9) hold for each subpart of each corresponding partition of
![]() $J_s$
for
$J_s$
for
![]() $s=1,\dots , m$
.
$s=1,\dots , m$
.
We let
![]() $H_{\mathcal {P}}$
be the subgroup of
$H_{\mathcal {P}}$
be the subgroup of
![]() ${\mathbb Z}^r$
defined as in [Reference Laurent8, page 319], that is,
${\mathbb Z}^r$
defined as in [Reference Laurent8, page 319], that is,
![]() $H_{\mathcal {P}}$
consists of all
$H_{\mathcal {P}}$
consists of all
![]() $\overline {n}\in {\mathbb Z}^r$
with the property that for each
$\overline {n}\in {\mathbb Z}^r$
with the property that for each
![]() $s=1,\dots , m$
and for each
$s=1,\dots , m$
and for each
![]() $i=1,\dots , v_s$
,
$i=1,\dots , v_s$
,
According to [Reference Laurent8, Theorem 6],
![]() $H_{\mathcal {P}}$
cannot be the trivial subgroup of
$H_{\mathcal {P}}$
cannot be the trivial subgroup of
![]() ${\mathbb Z}^r$
since we assumed there exists an infinite set
${\mathbb Z}^r$
since we assumed there exists an infinite set
![]() $\mathcal {S}$
of solutions
$\mathcal {S}$
of solutions
![]() $\overline {n}$
maximally compatible with respect to
$\overline {n}$
maximally compatible with respect to
![]() $\mathcal {P}$
. So, from now on, we assume there exists some nontrivial
$\mathcal {P}$
. So, from now on, we assume there exists some nontrivial
![]() $\overline {n}^{(0)}\in H_{\mathcal {P}}$
(that is, not all the entries of
$\overline {n}^{(0)}\in H_{\mathcal {P}}$
(that is, not all the entries of
![]() $\overline {n}^{(0)}$
are equal to
$\overline {n}^{(0)}$
are equal to
![]() $0$
). Without loss of generality, we assume that
$0$
). Without loss of generality, we assume that
Equation (3.10) says that for each
![]() $s=1,\dots ,m$
and for each
$s=1,\dots ,m$
and for each
![]() $i=1,\dots , v_s$
,
$i=1,\dots , v_s$
,
 $$ \begin{align} \bigg(\overline{\lambda}^{\overline{j}}\bigg)^{\overline{n}^{(0)}} \text{ is the same as we vary }\overline{j}\in J_{s,i}. \end{align} $$
$$ \begin{align} \bigg(\overline{\lambda}^{\overline{j}}\bigg)^{\overline{n}^{(0)}} \text{ is the same as we vary }\overline{j}\in J_{s,i}. \end{align} $$
We fix some
![]() $s\in \{1,\dots , m\}$
and also some
$s\in \{1,\dots , m\}$
and also some
![]() $i\in \{1,\dots , v_s\}$
; then we write each
$i\in \{1,\dots , v_s\}$
; then we write each
![]() $\overline {j}\in J_{s,i}$
as we did before:
$\overline {j}\in J_{s,i}$
as we did before:
![]() $\overline {j}:=(j_{1,1},j_{1,2},\dots ,j_{1,\ell _1},j_{2,1},j_{2,2}, \dots , j_{2,\ell _2},\dots ,j_{r,1},j_{r,2},\dots , j_{r,\ell _r})$
. Re-writing (3.11) using the index notation as in (3.5), we see that
$\overline {j}:=(j_{1,1},j_{1,2},\dots ,j_{1,\ell _1},j_{2,1},j_{2,2}, \dots , j_{2,\ell _2},\dots ,j_{r,1},j_{r,2},\dots , j_{r,\ell _r})$
. Re-writing (3.11) using the index notation as in (3.5), we see that
 $$ \begin{align} \prod_{p=1}^r \prod_{u=1}^{\ell_p} \lambda_{p,u}^{j_{p,u}\cdot n^{(0)}_p}\text{ is constant as we vary}\ \overline{j}\in J_{s,i}. \end{align} $$
$$ \begin{align} \prod_{p=1}^r \prod_{u=1}^{\ell_p} \lambda_{p,u}^{j_{p,u}\cdot n^{(0)}_p}\text{ is constant as we vary}\ \overline{j}\in J_{s,i}. \end{align} $$
Since the
![]() $\lambda _{p,u}$
are multiplicatively independent and also,
$\lambda _{p,u}$
are multiplicatively independent and also,
![]() $n^{(0)}_1\ne 0$
, it follows from (3.12) that for each
$n^{(0)}_1\ne 0$
, it follows from (3.12) that for each
![]() $s=1,\dots , m$
and for each
$s=1,\dots , m$
and for each
![]() $i=1,\dots , v_s$
, the vector
$i=1,\dots , v_s$
, the vector
We let
![]() $\overline {n}^{(1)}\in \mathcal {S}$
and write (3.9) for
$\overline {n}^{(1)}\in \mathcal {S}$
and write (3.9) for
![]() $\overline {n}:=\overline {n}^{(1)}$
. It follows that, for each
$\overline {n}:=\overline {n}^{(1)}$
. It follows that, for each
![]() $s\in \{1,\dots , m\}$
and for each
$s\in \{1,\dots , m\}$
and for each
![]() $i\in \{1,\dots , v_s\}$
,
$i\in \{1,\dots , v_s\}$
,
 $$ \begin{align*} \sum_{\overline{j}\in J_{s,i}}\prod_{p=1}^r\prod_{u=1}^{\ell_p} \lambda_{p,u}^{j_{p,u}\cdot n_p^{(1)}} Q_{s,\overline{j}}(\overline{n}^{(1)})=0, \end{align*} $$
$$ \begin{align*} \sum_{\overline{j}\in J_{s,i}}\prod_{p=1}^r\prod_{u=1}^{\ell_p} \lambda_{p,u}^{j_{p,u}\cdot n_p^{(1)}} Q_{s,\overline{j}}(\overline{n}^{(1)})=0, \end{align*} $$
where
![]() $\overline {n}^{(1)}:=(n_1^{(1)},\dots , n_r^{(1)})$
. Using (3.13), we divide (3.9) by
$\overline {n}^{(1)}:=(n_1^{(1)},\dots , n_r^{(1)})$
. Using (3.13), we divide (3.9) by
 $$ \begin{align*}\prod_{u=1}^{\ell_1} \lambda_{1,u}^{j_{1,u}\cdot n^{(1)}_1}\end{align*} $$
$$ \begin{align*}\prod_{u=1}^{\ell_1} \lambda_{1,u}^{j_{1,u}\cdot n^{(1)}_1}\end{align*} $$
and therefore,
 $$ \begin{align} \sum_{\overline{j}\in J_{s,i}} \prod_{p=2}^r \prod_{u=1}^{\ell_p} \lambda_{p,u}^{j_{p,u}\cdot n^{(1)}_p} \cdot Q_{s,\overline{j}}(\overline{n}^{(1)})=0. \end{align} $$
$$ \begin{align} \sum_{\overline{j}\in J_{s,i}} \prod_{p=2}^r \prod_{u=1}^{\ell_p} \lambda_{p,u}^{j_{p,u}\cdot n^{(1)}_p} \cdot Q_{s,\overline{j}}(\overline{n}^{(1)})=0. \end{align} $$
We write
![]() $\overline {y}^{(1)}:=\sum _{i=1}^r n^{(1)}_i\cdot \overline {b}_i\in \mathbb {G}_a^k(K)$
. Specialising
$\overline {y}^{(1)}:=\sum _{i=1}^r n^{(1)}_i\cdot \overline {b}_i\in \mathbb {G}_a^k(K)$
. Specialising
![]() $\overline {y}$
to
$\overline {y}$
to
![]() $\overline {y}^{(1)}$
in (3.3), we re-write that equation (for each
$\overline {y}^{(1)}$
in (3.3), we re-write that equation (for each
![]() $s=1,\dots , m$
) according to the given partition
$s=1,\dots , m$
) according to the given partition
![]() $\mathcal {P}_s$
of
$\mathcal {P}_s$
of
![]() $J_s$
as follows (see also the way we re-wrote (3.5) as (3.6)):
$J_s$
as follows (see also the way we re-wrote (3.5) as (3.6)):
 $$ \begin{align} f_s(\overline{x},\overline{y}^{(1)})=\sum_{i=1}^{v_s} \sum_{\overline{j}\in J_{s,i}} (\overline{x})^{\overline{j}}\cdot P_{s,\overline{j}}(\overline{y}^{(1)}). \end{align} $$
$$ \begin{align} f_s(\overline{x},\overline{y}^{(1)})=\sum_{i=1}^{v_s} \sum_{\overline{j}\in J_{s,i}} (\overline{x})^{\overline{j}}\cdot P_{s,\overline{j}}(\overline{y}^{(1)}). \end{align} $$
In (3.15), we have (as before)
![]() $(\overline {x})^{\overline {j}}:=\prod _{p=1}^r\prod _{u=1}^{\ell _p} x_{p,u}^{j_{p,u}}$
. Using (3.13) and (3.14) (for each
$(\overline {x})^{\overline {j}}:=\prod _{p=1}^r\prod _{u=1}^{\ell _p} x_{p,u}^{j_{p,u}}$
. Using (3.13) and (3.14) (for each
![]() $s=1,\dots , m$
and each
$s=1,\dots , m$
and each
![]() $i=1,\dots , v_s$
), and specialising further in (3.15) each
$i=1,\dots , v_s$
), and specialising further in (3.15) each
we see that
for any
![]() $x_{1,1},\dots , x_{1,\ell _1}$
. Thus, (3.16) tells us that V contains the entire subvariety of
$x_{1,1},\dots , x_{1,\ell _1}$
. Thus, (3.16) tells us that V contains the entire subvariety of
![]() $\mathbb {G}_m^\ell \times \mathbb {G}_a^k=T_1\times \cdots T_r\times \mathbb {G}_a^k$
given by
$\mathbb {G}_m^\ell \times \mathbb {G}_a^k=T_1\times \cdots T_r\times \mathbb {G}_a^k$
given by
thus contradicting the hypothesis from Theorem 2.7. Therefore, indeed, we only have finitely many solutions to the system of polynomial-exponential equations (3.6). This concludes our proof of Theorem 2.7.
4. Proof of Theorem 2.2
In this section, we work with the notation and the hypotheses from Theorem 2.2 to prove it.
By base-changing from K to the algebraic closure
![]() $\overline {K}$
, we may assume K is algebraically closed and
$\overline {K}$
, we may assume K is algebraically closed and
![]() $A=\operatorname {\mathrm {Mat}}_n(K)$
is the matrix algebra for some
$A=\operatorname {\mathrm {Mat}}_n(K)$
is the matrix algebra for some
![]() $n\geq 1$
, so that
$n\geq 1$
, so that
![]() $f_1,\dots ,f_r\in \operatorname {\mathrm {GL}}_n(K)$
. Note that the eigenvalues of
$f_1,\dots ,f_r\in \operatorname {\mathrm {GL}}_n(K)$
. Note that the eigenvalues of
![]() $L_{f_i}$
are just the eigenvalues of
$L_{f_i}$
are just the eigenvalues of
![]() $f_i$
repeated n times, so
$f_i$
repeated n times, so
![]() $\Lambda _{f_i}$
is simply the set of eigenvalues of
$\Lambda _{f_i}$
is simply the set of eigenvalues of
![]() $f_i$
(not counting multiplicities).
$f_i$
(not counting multiplicities).
Consider the commutative K-subalgebra
![]() $K[f_i]$
of
$K[f_i]$
of
![]() $\operatorname {\mathrm {Mat}}_n(K)$
generated by
$\operatorname {\mathrm {Mat}}_n(K)$
generated by
![]() $f_i$
. We have commutative linear algebraic groups
$f_i$
. We have commutative linear algebraic groups
![]() $G_i:=K[f_i]^\times $
and
$G_i:=K[f_i]^\times $
and
![]() $G:=G_1\times \dots \times G_r$
. Let
$G:=G_1\times \dots \times G_r$
. Let
![]() $g_i$
be the element
$g_i$
be the element
![]() $(1,\dots ,f_i,\dots ,1)$
in G and let
$(1,\dots ,f_i,\dots ,1)$
in G and let
![]() $\Gamma '$
be the subgroup of G generated by
$\Gamma '$
be the subgroup of G generated by
![]() $g_1,\dots ,g_r$
.
$g_1,\dots ,g_r$
.
Over an algebraically closed field K, any commutative linear algebraic group is necessarily of the form
![]() $\mathbb {G}_m^\ell \times \mathbb {G}_a^u$
with
$\mathbb {G}_m^\ell \times \mathbb {G}_a^u$
with
![]() $\ell ,u\geq 0$
. Indeed, one has a direct product decomposition into the semisimple part (which gives a torus) and the unipotent part. For a commutative unipotent group, the exponential map is an isomorphism of algebraic groups, so the unipotent part is of the form
$\ell ,u\geq 0$
. Indeed, one has a direct product decomposition into the semisimple part (which gives a torus) and the unipotent part. For a commutative unipotent group, the exponential map is an isomorphism of algebraic groups, so the unipotent part is of the form
![]() $\mathbb {G}_a^u$
.
$\mathbb {G}_a^u$
.
Next, we will be more explicit regarding each algebraic group
![]() $G_i$
. Let
$G_i$
. Let
![]() $\Lambda _{f_i}=\{{\lambda _{i,1},\dots ,\lambda _{i,\ell _i}}\}$
and let
$\Lambda _{f_i}=\{{\lambda _{i,1},\dots ,\lambda _{i,\ell _i}}\}$
and let
![]() $G_i=T_i\times U_i$
, where
$G_i=T_i\times U_i$
, where
![]() $T_i$
is the semisimple part and
$T_i$
is the semisimple part and
![]() $U_i$
is the unipotent part. Using the Jordan canonical form of
$U_i$
is the unipotent part. Using the Jordan canonical form of
![]() $f_i$
, we have an isomorphism
$f_i$
, we have an isomorphism
![]() $T_i\simeq (K^\times )^{\ell _i}$
, such that the image of
$T_i\simeq (K^\times )^{\ell _i}$
, such that the image of
![]() $f_i$
projected onto
$f_i$
projected onto
![]() $T_i$
is identified with
$T_i$
is identified with
![]() $(\lambda _{i,1},\dots ,\lambda _{i,\ell _i})$
.
$(\lambda _{i,1},\dots ,\lambda _{i,\ell _i})$
.
Let
![]() $U:=U_1\times \dots \times U_r\simeq \mathbb {G}_a^u$
and
$U:=U_1\times \dots \times U_r\simeq \mathbb {G}_a^u$
and
![]() $T:=T_1\times \dots \times T_r$
. From the above discussion, we get an isomorphism
$T:=T_1\times \dots \times T_r$
. From the above discussion, we get an isomorphism
![]() $G= T\times U\simeq \mathbb {G}_m^{\ell _1+\dots +\ell _r} \times \mathbb {G}_a^u$
under which
$G= T\times U\simeq \mathbb {G}_m^{\ell _1+\dots +\ell _r} \times \mathbb {G}_a^u$
under which
![]() $g_1,\dots ,g_r$
takes the form of (2.2) for some
$g_1,\dots ,g_r$
takes the form of (2.2) for some
![]() $v_1,\dots ,v_r\in K^u$
. Since
$v_1,\dots ,v_r\in K^u$
. Since
![]() $f_1,\dots ,f_r$
have multiplicatively independent eigenvalues,
$f_1,\dots ,f_r$
have multiplicatively independent eigenvalues,
![]() $\lambda _{i,j}$
are multiplicatively independent. Thus,
$\lambda _{i,j}$
are multiplicatively independent. Thus,
![]() $\Gamma '\subseteq G$
is strongly independent in the sense of Definition 2.6.
$\Gamma '\subseteq G$
is strongly independent in the sense of Definition 2.6.
Define an algebraic map (not necessarily a group homomorphism)
where the multiplication takes place in
![]() $\operatorname {\mathrm {GL}}_n(K)$
, and let
$\operatorname {\mathrm {GL}}_n(K)$
, and let
![]() $W:=\mu ^{-1}(V)$
, which is a closed subvariety of G. We claim that W does not contain a subvariety of the form
$W:=\mu ^{-1}(V)$
, which is a closed subvariety of G. We claim that W does not contain a subvariety of the form
![]() $T_i\times \{{v}\}$
for some
$T_i\times \{{v}\}$
for some
![]() $i\in \{1,\dots , r\}$
and some
$i\in \{1,\dots , r\}$
and some
![]() $v\in (\prod _{j\ne i}T_j)\times U$
.
$v\in (\prod _{j\ne i}T_j)\times U$
.
We argue by contradiction. Without loss of generality, assume that
![]() $T_1\times \{{v}\}\subseteq W$
for some
$T_1\times \{{v}\}\subseteq W$
for some
![]() $v\in (\prod _{i=2}^rT_i)\times U$
. Consider the canonical map
$v\in (\prod _{i=2}^rT_i)\times U$
. Consider the canonical map
![]() $\tau _1:K^\times \hookrightarrow G_1\subseteq \operatorname {\mathrm {GL}}_n(K)$
given by the scalar matrices. Then,
$\tau _1:K^\times \hookrightarrow G_1\subseteq \operatorname {\mathrm {GL}}_n(K)$
given by the scalar matrices. Then,
![]() $\tau _1$
in fact maps into
$\tau _1$
in fact maps into
![]() $T_1=(K^\times )^{\ell _1}$
and takes the form
$T_1=(K^\times )^{\ell _1}$
and takes the form
![]() $\tau _1(c)=(c,\dots ,c)$
. A crucial property of
$\tau _1(c)=(c,\dots ,c)$
. A crucial property of
![]() $\mu $
is that it behaves well with scalar multiplication: for
$\mu $
is that it behaves well with scalar multiplication: for
![]() $c\in K^\times $
and
$c\in K^\times $
and
![]() $(z_1,\dots ,z_r)\in G=G_1\times \dots \times G_r$
,
$(z_1,\dots ,z_r)\in G=G_1\times \dots \times G_r$
,
Now we pick
![]() $(z_1,\dots ,z_r)\in G$
that lies in
$(z_1,\dots ,z_r)\in G$
that lies in
![]() $T_1\times \{{v}\}$
under the identification
$T_1\times \{{v}\}$
under the identification
![]() $G= T\times U$
. For all
$G= T\times U$
. For all
![]() $c\in K^\times $
, since
$c\in K^\times $
, since
![]() $T_1\times \{{v}\}$
is a
$T_1\times \{{v}\}$
is a
![]() $T_1$
-coset of G and
$T_1$
-coset of G and
![]() $\tau _1(c)\in T_1\subseteq T$
, it follows that
$\tau _1(c)\in T_1\subseteq T$
, it follows that
![]() $\tau _1(c)\cdot (z_1,\dots ,z_r)\in T_1\times \{{v}\}$
. Since
$\tau _1(c)\cdot (z_1,\dots ,z_r)\in T_1\times \{{v}\}$
. Since
![]() $T_1\times \{{v}\}\subseteq W$
, applying
$T_1\times \{{v}\}\subseteq W$
, applying
![]() $\mu $
gives
$\mu $
gives
As V is Zariski closed in
![]() $\operatorname {\mathrm {Mat}}_n(K)$
, we have
$\operatorname {\mathrm {Mat}}_n(K)$
, we have
![]() $0\in V$
, contradicting the hypothesis from Theorem 2.2. This proves the claim.
$0\in V$
, contradicting the hypothesis from Theorem 2.2. This proves the claim.
Finally, since the assumptions of Theorem 2.7 are verified,
![]() $\lvert {W(K)\cap \Gamma '\rvert }<\infty $
. Applying
$\lvert {W(K)\cap \Gamma '\rvert }<\infty $
. Applying
![]() $\mu $
, this means
$\mu $
, this means
![]() $f_1^{n_1}\cdots f_r^{n_r}\in V$
for only finitely many
$f_1^{n_1}\cdots f_r^{n_r}\in V$
for only finitely many
![]() $(n_1,\dots ,n_r)\in {\mathbb Z}^r$
, so the conclusion of Theorem 2.2 is proved.
$(n_1,\dots ,n_r)\in {\mathbb Z}^r$
, so the conclusion of Theorem 2.2 is proved.
Acknowledgements
We thank Zinovy Reichstein for numerous helpful conversations. We thank the referee and also the editor for their comments.