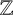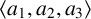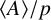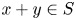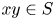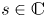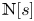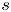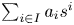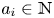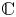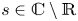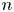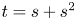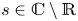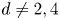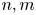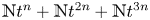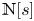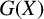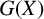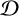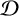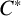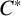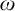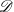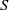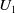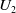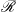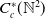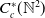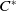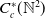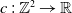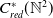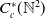272 results in 20Mxx
A CHARACTERISATION OF SEMIGROUPS WITH ONLY COUNTABLY MANY SUBDIRECT PRODUCTS WITH
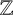 $\mathbb {Z}$
$\mathbb {Z}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
KRONECKER COEFFICIENTS FOR (DUAL) SYMMETRIC INVERSE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-26
-
- Article
-
- You have access
- HTML
- Export citation
ON THE SET OF BETTI ELEMENTS OF A PUISEUX MONOID
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-13
-
- Article
-
- You have access
- HTML
- Export citation
Minimal monoids generating varieties with complex subvariety lattices
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 March 2024, pp. 617-642
-
- Article
-
- You have access
- HTML
- Export citation
GENERATING FUNCTIONS FOR THE QUOTIENTS OF NUMERICAL SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
Invariant set generated by a nonreal number is everywhere dense
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MAXIMAL SUBSEMIGROUPS OF INFINITE SYMMETRIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 324-337
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
NORMAL SUBMONOIDS AND CONGRUENCES ON A MONOID
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 331-362
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
FINITELY PRESENTED INVERSE SEMIGROUPS WITH FINITELY MANY IDEMPOTENTS IN EACH
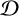 $\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS
$\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 384-398
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON GROUPS OF UNITS OF SPECIAL AND ONE-RELATOR INVERSE MONOIDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 21 November 2023, pp. 1875-1918
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ZARISKI TOPOLOGY ON ENDOMORPHISM MONOIDS OF OMEGA-CATEGORICAL STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 31 October 2023, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prefix monoids of groups and right units of special inverse monoids
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 30 October 2023, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE BASIS PROBLEM FOR INVOLUTION MONOIDS OF ORDER FIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 350-364
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Proper Ehresmann semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 758-788
-
- Article
-
- You have access
- HTML
- Export citation
Corrigendum: Von Neumann algebras and extensions of inverse semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 919-922
-
- Article
-
- You have access
- HTML
- Export citation
Tame or wild Toeplitz shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 August 2023, pp. 1379-1417
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the structure of lower bounded HNN extensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 August 2023, pp. 697-715
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perfection for semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 259-287
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterisation of atomicity
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 459-465
- Print publication:
- September 2023
-
- Article
-
- You have access
- HTML
- Export citation
KMS states on
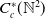 $C_c^{*}(\mathbb{N}^2)$
$C_c^{*}(\mathbb{N}^2)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 501-528
- Print publication:
- September 2023
-
- Article
-
- You have access
- HTML
- Export citation