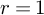1 Introduction and summary of results
The purpose of this paper is to undertake a systematic investigation into the groups of units of one-relator and special inverse monoids. Throughout, there is a particular emphasis on comparing and contrasting these groups with groups of units of special monoids, after the work of Adjan, Makanin, Lallement and Zhang, as well as with one-relator groups themselves (see [Reference Adjan1, Reference Lallement14, Reference Makanin20, Reference Zhang29]).
The word problem for semigroups defined by a single relation is one of the oldest, most famous and most elementary to state open problems in the broad area of combinatorial algebra. It asks whether for every monoid of the form
![]() $M={\operatorname {Mon}\bigl \langle {A}\:|\:{u=v} \bigr \rangle }$
, that is defined by generators A and a single defining relation
$M={\operatorname {Mon}\bigl \langle {A}\:|\:{u=v} \bigr \rangle }$
, that is defined by generators A and a single defining relation
![]() $u=v$
, there is an algorithm which for any two words
$u=v$
, there is an algorithm which for any two words
![]() $w_1,w_2\in A^\ast $
decides whether or not
$w_1,w_2\in A^\ast $
decides whether or not
![]() $w_1=w_2$
in M. In his seminal work on the subject in the 1960s and 1970s, Adjan proved, among other things, the following:
$w_1=w_2$
in M. In his seminal work on the subject in the 1960s and 1970s, Adjan proved, among other things, the following:
-
(A1) The word problem is soluble for every one-relator special monoid, that is monoid defined by
 $M={\operatorname {Mon}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
(see [Reference Adjan1]).
$M={\operatorname {Mon}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
(see [Reference Adjan1]). -
(A2) The word problem is soluble for every monoid of the form
 $M={\operatorname {Mon}\bigl \langle {A}\:|\:{u=v} \bigr \rangle }$
, where
$M={\operatorname {Mon}\bigl \langle {A}\:|\:{u=v} \bigr \rangle }$
, where
 $u,v$
are nonempty words whose first letters are distinct and last letters are distinct (see [Reference Adjan1]).
$u,v$
are nonempty words whose first letters are distinct and last letters are distinct (see [Reference Adjan1]). -
(A3) If the word problem is soluble for all monoids of the form
 $M={\operatorname {Mon}\bigl \langle {A}\:|\:{au=av} \bigr \rangle }$
, where
$M={\operatorname {Mon}\bigl \langle {A}\:|\:{au=av} \bigr \rangle }$
, where
 $a\in A$
, and the final letters of u and v are distinct, then the word problem for all one relation monoids is soluble; with Oganesjan [Reference Adjan and Oganesjan2].
$a\in A$
, and the final letters of u and v are distinct, then the word problem for all one relation monoids is soluble; with Oganesjan [Reference Adjan and Oganesjan2].
Adjan’s proof of (A1) and some subsequent developments are of particular relevance for our work, and we outline them here. The key feature is a focus on the group of units. Specifically, suppose r is decomposed as
![]() $r\equiv r_1\dots r_k$
, where
$r\equiv r_1\dots r_k$
, where
![]() $r_i$
are nonempty and invertible and of shortest possible length subject to this requirement; we will call such
$r_i$
are nonempty and invertible and of shortest possible length subject to this requirement; we will call such
![]() $r_i$
the minimal invertible pieces of r. Then the following holds:
$r_i$
the minimal invertible pieces of r. Then the following holds:
Theorem 1.1 (Adjan [Reference Adjan1])
If
![]() $M={\operatorname {Mon}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, and if
$M={\operatorname {Mon}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, and if
![]() $r=r_1\dots r_k$
is the decomposition into minimal invertible pieces, then the group of units
$r=r_1\dots r_k$
is the decomposition into minimal invertible pieces, then the group of units
![]() $U=U(M)$
of M is generated by
$U=U(M)$
of M is generated by
![]() $\{r_1,\dots ,r_k\}$
. Furthermore, if B is an alphabet in one-one correspondence
$\{r_1,\dots ,r_k\}$
. Furthermore, if B is an alphabet in one-one correspondence
![]() $r_i\mapsto \overline {r}_i$
with the set
$r_i\mapsto \overline {r}_i$
with the set
![]() $\{r_1,\dots , r_k\}$
, then the group presentation
$\{r_1,\dots , r_k\}$
, then the group presentation
![]() ${\operatorname {Gp}\bigl \langle {B}\:|\:{\overline {r}_1\dots \overline {r}_n=1} \bigr \rangle }$
defines U with respect to this generating set.
${\operatorname {Gp}\bigl \langle {B}\:|\:{\overline {r}_1\dots \overline {r}_n=1} \bigr \rangle }$
defines U with respect to this generating set.
It follows then that the group of units of M is a one-relator group, and hence has a soluble word problem by a classical result of Magnus (see [Reference Lyndon and Schupp18, Reference Magnus, Karrass and Solitar19]). It can be shown that the submonoid of right units R of M is the free product of U and a free monoid of finite rank, and hence, it is also finitely presented and has a soluble word problem. A further normal form theorem can be proved that reduces the word problem for the entire monoid M to those of U and R, and thus M has a soluble word problem too.
Makanin [Reference Makanin20] generalises this approach to special monoids, that is monoids defined by presentations of the form
![]() $M={\operatorname {Mon}\bigl \langle {A}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
. This time we decompose each
$M={\operatorname {Mon}\bigl \langle {A}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
. This time we decompose each
![]() $r_i$
into minimal invertible pieces
$r_i$
into minimal invertible pieces
![]() $r_i\equiv r_{i1}\dots r_{ik_i}$
. Furthermore, we assign to each piece
$r_i\equiv r_{i1}\dots r_{ik_i}$
. Furthermore, we assign to each piece
![]() $r_{ij}$
a new letter
$r_{ij}$
a new letter
![]() $\overline {r}_{ij}$
, but this time in such a way that
$\overline {r}_{ij}$
, but this time in such a way that
![]() $\overline {r}_{ij}=\overline {r}_{lm}$
whenever
$\overline {r}_{ij}=\overline {r}_{lm}$
whenever
![]() $r_{ij}=r_{lm}$
in the monoid M. Collecting these new letters into the alphabet B, we have:
$r_{ij}=r_{lm}$
in the monoid M. Collecting these new letters into the alphabet B, we have:
Theorem 1.2 (Makanin [Reference Makanin20])
The group of units of
![]() $M={\operatorname {Mon}\bigl \langle {A}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
is generated by the set
$M={\operatorname {Mon}\bigl \langle {A}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
is generated by the set
![]() $\{ r_{ij}\::\: i\in I,\ 1\leq j\leq k_i\}$
, and, in terms of these generators, is defined by the presentation
$\{ r_{ij}\::\: i\in I,\ 1\leq j\leq k_i\}$
, and, in terms of these generators, is defined by the presentation
![]() ${\operatorname {Gp}\bigl \langle {B}\:|\:{\overline {r}_{i1}\dots \overline {r}_{ik_i}=1\ (i\in I)} \bigr \rangle }$
.
${\operatorname {Gp}\bigl \langle {B}\:|\:{\overline {r}_{i1}\dots \overline {r}_{ik_i}=1\ (i\in I)} \bigr \rangle }$
.
It follows that the group of units of a special monoid can be defined by a presentation with no more defining relations than the original presentation for M.
A key property of the decompositions into minimal invertible pieces is that they do not overlap with each other. This in fact yields an algorithm, which will be referred to as the Adjan overlap algorithm, for computing the decomposition into minimal invertible pieces for one-relator monoids (see Lallement [Reference Lallement14]). The algorithm proceeds by finding the overlaps of r with itself, forming certain cyclic conjugates of r and then repeating this process. This algorithm also makes sense in the context of special monoids too, and it computes some decomposition of the relators into invertible pieces. It turns out, however, that these pieces need not be minimal in general (see Example 4.2). All the results surveyed above concerning special monoids were revisited and simplified by Zhang [Reference Zhang29, Reference Zhang30] using the methodology of string rewriting systems.
In a separate strand, the 1990s and early 2000s saw a dynamic development of the theory of presentations for inverse monoids. The catalyst for this was Stephen’s discovery [Reference Stephen25] of an algorithmic procedure, akin to the Todd–Coxeter algorithm from combinatorial group theory, which computes the so called Schützenberger graph of an inverse monoid
![]() $M={\operatorname {Inv}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
based at an arbitrary word
$M={\operatorname {Inv}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
based at an arbitrary word
![]() $w\in \overline {A}^\ast $
. Linking this development with (A3), Ivanov et al. [Reference Ivanov, Margolis and Meakin12] showed that if all one-relator inverse monoids
$w\in \overline {A}^\ast $
. Linking this development with (A3), Ivanov et al. [Reference Ivanov, Margolis and Meakin12] showed that if all one-relator inverse monoids
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, where r is a reduced word, have soluble word problems, then this would imply the same for the monoids of the form
${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, where r is a reduced word, have soluble word problems, then this would imply the same for the monoids of the form
![]() $M={\operatorname {Mon}\bigl \langle {A}\:|\:{au=av} \bigr \rangle }$
, and hence for all one-relation monoids. Relating to this, it was recently shown in [Reference Gray6] that, in general, not every one-relator inverse monoid
$M={\operatorname {Mon}\bigl \langle {A}\:|\:{au=av} \bigr \rangle }$
, and hence for all one-relation monoids. Relating to this, it was recently shown in [Reference Gray6] that, in general, not every one-relator inverse monoid
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
has soluble word problems. However, the question of solubility of the word problem in the case that r is a reduced word is still open. In their paper [Reference Ivanov, Margolis and Meakin12], Ivanov et al. also essentially proved the generation part of the analogue of Theorem 1.2 for special inverse monoids:
${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
has soluble word problems. However, the question of solubility of the word problem in the case that r is a reduced word is still open. In their paper [Reference Ivanov, Margolis and Meakin12], Ivanov et al. also essentially proved the generation part of the analogue of Theorem 1.2 for special inverse monoids:
Theorem 1.3 (Ivanov et al. [Reference Ivanov, Margolis and Meakin12, Proposition 4.2])
Suppose
is a special inverse monoid, and that each relator
![]() $r_i$
is decomposed into minimal invertible pieces
$r_i$
is decomposed into minimal invertible pieces
![]() $r_i\equiv r_{i1}\dots r_{ik_i}$
. Then the set
$r_i\equiv r_{i1}\dots r_{ik_i}$
. Then the set
![]() $\{ r_{ij}\::\: i\in I,\ 1\leq j\leq k_i\}$
generates the group of units of M.
$\{ r_{ij}\::\: i\in I,\ 1\leq j\leq k_i\}$
generates the group of units of M.
Proof. The authors state their theorem under the assumption that all
![]() $r_i$
are cyclically reduced words. However, on inspection, this condition is not used in the proof, and hence, their proof in fact establishes the theorem as stated here.
$r_i$
are cyclically reduced words. However, on inspection, this condition is not used in the proof, and hence, their proof in fact establishes the theorem as stated here.
However, there has been no further development along the Adjan/Makanin/Zhang lines, towards establishing presentation properties of the group of units. In fact, partly to hint at the difficulties that such an attempt would entail, Margolis et al. [Reference Margolis, Meakin and Stephen22] introduce the following specific one-relator monoid
which has since come to be known as the O’Hare monoid. It is defined by a single, positive relator r (and hence, in particular, it is E-unitary). The relator has no overlaps with itself, so the Adjan overlap algorithm would terminate instantly, and return r as a single invertible piece of itself. However, using van Kampen diagrams and Stephen’s procedure, Margolis and Meakin succeed in showing that r in fact has a finer decomposition, namely
They provide no further information about the group of units.
Motivated by the developments described above, in this paper, we investigate the extent to which the Adjan/Makanin/Zhang results for groups of units, and monoids of right units, of one-relator and special monoids are also valid for one-relator and special inverse monoids. In a nutshell, we will see that they do often, but not always. Exploration of when they do will lead us to a general theorem, and several applications in concrete situations with extra assumptions. On the negative side, we will see that the results may fail to generalise to inverse semigroups for each of two possible reasons: the group defined by the natural presentation on the minimal invertible pieces may not be isomorphic to the group of units, and there are inherent structural difficulties in attempting to compute the minimal pieces.
To elaborate a bit further, we consider the question of whether the group of units of a one-relator inverse monoid is a one-relator group. In the positive direction, in Section 3, we prove the following general sufficient condition for this to be the case:
Theorem 3.1. Let
![]() $M= {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
be a special inverse monoid, let
$M= {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
be a special inverse monoid, let
![]() ${r_{i}\equiv r_{i 1}r_{i 2}\ldots r_{i k_i}} $
be a factorisation into invertible pieces for
${r_{i}\equiv r_{i 1}r_{i 2}\ldots r_{i k_i}} $
be a factorisation into invertible pieces for
![]() $i\in I$
, and let H be the subgroup of the free group
$i\in I$
, and let H be the subgroup of the free group
![]() $F_A$
generated by all the pieces
$F_A$
generated by all the pieces
![]() $r_{ij} \; ( i\in I, 1\leq j\leq k_{i} ) $
. Fix an isomorphism
$r_{ij} \; ( i\in I, 1\leq j\leq k_{i} ) $
. Fix an isomorphism
![]() $\phi :F_Y \rightarrow H$
, and set
$\phi :F_Y \rightarrow H$
, and set
If
![]() $\phi $
induces an embedding of the group
$\phi $
induces an embedding of the group
![]() $ K$
into the group
$ K$
into the group
![]() ${\operatorname {Gp}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
defined by the same presentation as M, then
${\operatorname {Gp}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
defined by the same presentation as M, then
![]() $\phi $
induces an isomorphism between K and the subgroup of the monoid M generated by the pieces.
$\phi $
induces an isomorphism between K and the subgroup of the monoid M generated by the pieces.
We note that this result is valid for special inverse monoids in general, and that it enables one to reduce the original question to a question purely referring to the corresponding groups and their subgroups. In particular, our questions concerning one-relator inverse monoids are reduced to questions about subgroups of one-relator groups. We therefore go on to prove a number of results in which we identify situations where the conditions of the theorem are met. As a consequence, in Section 5, we exhibit several families of one-relator inverse monoids whose groups of units are all one-relator. In particular, we are able to prove that the group of units of the O’Hare monoid
![]() ${\mathcal {O}}$
is the free group of rank
${\mathcal {O}}$
is the free group of rank
![]() $2$
.
$2$
.
It is natural to ask whether the assumptions of Theorem 3.1 are perhaps always satisfied, or at least always in the case of one-relator presentations. The answer to this is negative, and in order to show this, we give a general construction in Section 6 which we then apply in Section 7 to demonstrate the following:
-
• There exists a one-relator special inverse monoid whose group of units is not one-relator (with respect to any generating set).
-
• There exists a finitely presented special inverse monoid whose group of units is not finitely presented.
-
• There exists a one-relator special inverse monoid with finitely presented group of units, and finitely generated but nonfinitely presented submonoid of right units.
-
• There exists a one-relator special inverse monoid whose submonoid of right units is not a free product of the groups of units and a free monoid (this follows from the previous point).
Also, using these results, at the end of Section 7, we will present several results which show the close relationship between the question of finite presentability of the groups of units of special one-relator inverse monoids, and an open problem of Baumslag [Reference Baumslag3, page 76] which asks whether every one-relator group is coherent. In particular, we show that the problem of proving coherence of all one-relator groups is equivalent to the problem of showing that the group of units of an E-unitary one-relator special inverse monoid is always finitely presented.
Throughout the paper, the decompositions of relators into invertible pieces play a pivotal role, and we discuss them in their own right in Section 4. Applying a result of Narendran et al. [Reference Narendran, Ó’Dúnlang and Otto23], we observe that, unlike the situation in one-relator monoids, for general special monoids, there is no algorithm to compute the decomposition into minimal invertible pieces. The existence of such an algorithm for one-relator special inverse monoids remains open. However, we present an algorithm which does compute a decomposition into invertible pieces. The decomposition computed by this algorithm is always at least as fine as that computed by the Adjan overlap algorithm, and, in fact, in all the examples known to us in the one-relator case, including the O’Hare monoid
![]() ${\mathcal {O}}$
, it computes the decomposition into minimal invertible pieces.
${\mathcal {O}}$
, it computes the decomposition into minimal invertible pieces.
2 Preliminaries
For an alphabet A, we will denote the free monoid over A by
![]() $A^\ast $
. It consists of all words over A, including the empty word
$A^\ast $
. It consists of all words over A, including the empty word
![]() $\epsilon =\epsilon _A$
. Since throughout words will play a somewhat ambivalent role of elements in a free monoid, as well as those in a monoid defined by a presentation, we will denote equality of words in
$\epsilon =\epsilon _A$
. Since throughout words will play a somewhat ambivalent role of elements in a free monoid, as well as those in a monoid defined by a presentation, we will denote equality of words in
![]() $A^\ast $
by
$A^\ast $
by
![]() $u\equiv v$
.
$u\equiv v$
.
A monoid presentation is a pair
![]() ${\operatorname {Mon}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
, where A is an alphabet and
${\operatorname {Mon}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
, where A is an alphabet and
![]() $R\subseteq A^\ast \times A^\ast $
is a set of pairs of words. This presentation defines the monoid
$R\subseteq A^\ast \times A^\ast $
is a set of pairs of words. This presentation defines the monoid
![]() $A^\ast /\rho $
, where
$A^\ast /\rho $
, where
![]() $\rho $
is the congruence on
$\rho $
is the congruence on
![]() $A^\ast $
generated by R. We will write
$A^\ast $
generated by R. We will write
![]() $M={\operatorname {Mon}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
. A typical relation
$M={\operatorname {Mon}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
. A typical relation
![]() $(u,v)\in R$
is usually written
$(u,v)\in R$
is usually written
![]() $u=v$
, and we extend this to pairs in
$u=v$
, and we extend this to pairs in
![]() $\rho $
. Thus, in the context of the monoid defined by a presentation,
$\rho $
. Thus, in the context of the monoid defined by a presentation,
![]() $u=v$
means that u and v, interpreted as products of generators, represent the same element of M. The monoid M is a natural homomorphic image of the free monoid
$u=v$
means that u and v, interpreted as products of generators, represent the same element of M. The monoid M is a natural homomorphic image of the free monoid
![]() $A^\ast $
via the mapping
$A^\ast $
via the mapping
![]() $w\mapsto w/\rho $
, called the natural homomorphism. The group of units
$w\mapsto w/\rho $
, called the natural homomorphism. The group of units
![]() $U(M)$
of a monoid M consists of all elements
$U(M)$
of a monoid M consists of all elements
![]() $x\in M$
which are (two-sided) invertible, that is for which there exists
$x\in M$
which are (two-sided) invertible, that is for which there exists
![]() $y\in M$
, such that
$y\in M$
, such that
![]() $xy=yx=1_M$
. A presentation
$xy=yx=1_M$
. A presentation
![]() ${\operatorname {Mon}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
is called special if every defining relation has the form
${\operatorname {Mon}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
is called special if every defining relation has the form
![]() $u=1$
. The word u in such a relation is often called a relator. A one-relator monoid is a monoid defined by a single relator, that is
$u=1$
. The word u in such a relation is often called a relator. A one-relator monoid is a monoid defined by a single relator, that is
![]() $M={\operatorname {Mon}\bigl \langle {A}\:|\:{u=1} \bigr \rangle }$
.
$M={\operatorname {Mon}\bigl \langle {A}\:|\:{u=1} \bigr \rangle }$
.
For an alphabet A, let
![]() $A^{-1}=\{ a^{-1}\::\: a\in A\}$
be another alphabet disjoint from A and in 1-1 correspondence with A. Further, let
$A^{-1}=\{ a^{-1}\::\: a\in A\}$
be another alphabet disjoint from A and in 1-1 correspondence with A. Further, let
![]() $\overline {A}=A\cup A^{-1}$
, and extend the bijection
$\overline {A}=A\cup A^{-1}$
, and extend the bijection
![]() $a\mapsto a^{-1}$
first to
$a\mapsto a^{-1}$
first to
![]() $\overline {A}$
by
$\overline {A}$
by
![]() $(a^{-1})^{-1}\equiv a$
, and then entire
$(a^{-1})^{-1}\equiv a$
, and then entire
![]() $\overline {A}^\ast $
by
$\overline {A}^\ast $
by
![]() $(a_1^{\epsilon _1}a_2^{\epsilon _2}\dots a_n^{\epsilon _n})^{-1} =a_n^{-\epsilon _1}\dots a_2^{-\epsilon _2}a_1^{-\epsilon _1}$
for
$(a_1^{\epsilon _1}a_2^{\epsilon _2}\dots a_n^{\epsilon _n})^{-1} =a_n^{-\epsilon _1}\dots a_2^{-\epsilon _2}a_1^{-\epsilon _1}$
for
![]() $a_i\in A$
,
$a_i\in A$
,
![]() $\epsilon _i=\pm 1$
. The free group
$\epsilon _i=\pm 1$
. The free group
![]() $F_A$
over A consists of all reduced words from
$F_A$
over A consists of all reduced words from
![]() $\overline {A}^\ast $
, that is words containing no subword of the form
$\overline {A}^\ast $
, that is words containing no subword of the form
![]() $aa^{-1}$
with
$aa^{-1}$
with
![]() $a\in \overline {A}$
, under multiplication
$a\in \overline {A}$
, under multiplication
![]() $u\cdot v=\operatorname {\mathrm {red}}(uv)$
. Here,
$u\cdot v=\operatorname {\mathrm {red}}(uv)$
. Here,
![]() $\operatorname {\mathrm {red}}(u)$
denotes the free reduction of u, that is the result of successively deleting all pairs
$\operatorname {\mathrm {red}}(u)$
denotes the free reduction of u, that is the result of successively deleting all pairs
![]() $aa^{-1}$
in u. It is well known that the order of performing these deletions is inconsequential. Sometimes we will write
$aa^{-1}$
in u. It is well known that the order of performing these deletions is inconsequential. Sometimes we will write
![]() $\operatorname {\mathrm {red}}_A$
for
$\operatorname {\mathrm {red}}_A$
for
![]() $\operatorname {\mathrm {red}}$
when we want to work with free reductions over different alphabets. We will also extend the use of
$\operatorname {\mathrm {red}}$
when we want to work with free reductions over different alphabets. We will also extend the use of
![]() $\operatorname {\mathrm {red}}$
to apply to sets of words:
$\operatorname {\mathrm {red}}$
to apply to sets of words:
![]() $\operatorname {\mathrm {red}}(W)=\{ \operatorname {\mathrm {red}}(w)\::\: w\in W\}$
.
$\operatorname {\mathrm {red}}(W)=\{ \operatorname {\mathrm {red}}(w)\::\: w\in W\}$
.
A group presentation is a pair
![]() ${\operatorname {Gp}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
, where A is an alphabet and
${\operatorname {Gp}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
, where A is an alphabet and
![]() $R\subseteq \overline {A}^\ast \times \{1\}$
. The group defined by presentation is
$R\subseteq \overline {A}^\ast \times \{1\}$
. The group defined by presentation is
![]() $G={\operatorname {Gp}\bigl \langle {A}\:|\:{R} \bigr \rangle }={\operatorname {Mon}\bigl \langle {\overline {A}}\:|\:{R,\ aa^{-1}=a^{-1}a=1\ (a\in A)} \bigr \rangle }$
. Alternatively, G can be viewed as the quotient
$G={\operatorname {Gp}\bigl \langle {A}\:|\:{R} \bigr \rangle }={\operatorname {Mon}\bigl \langle {\overline {A}}\:|\:{R,\ aa^{-1}=a^{-1}a=1\ (a\in A)} \bigr \rangle }$
. Alternatively, G can be viewed as the quotient
![]() $F_A/N$
, where N is the normal subgroup of
$F_A/N$
, where N is the normal subgroup of
![]() $F_A$
generated by all u, where
$F_A$
generated by all u, where
![]() $(u,1)\in R$
. Again, G is a homomorphic image of
$(u,1)\in R$
. Again, G is a homomorphic image of
![]() $F_A$
via the natural homomorphism
$F_A$
via the natural homomorphism
![]() $w\mapsto wN$
.
$w\mapsto wN$
.
The free inverse monoid over a set A will be denoted by
![]() $FI_A$
. It can be viewed as the monoid
$FI_A$
. It can be viewed as the monoid
An inverse monoid presentation is a pair
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
, where
${\operatorname {Inv}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
, where
![]() $R\subseteq \overline {A}^\ast \times \overline {A}^\ast $
. It defines the quotient
$R\subseteq \overline {A}^\ast \times \overline {A}^\ast $
. It defines the quotient
![]() $FI_A/\rho $
, where
$FI_A/\rho $
, where
![]() $\rho $
is the congruence generated by R, which is once again a natural homomorphic image of
$\rho $
is the congruence generated by R, which is once again a natural homomorphic image of
![]() $FI_A$
via
$FI_A$
via
![]() $w\mapsto w/\rho $
. If all the relations in R are of the form
$w\mapsto w/\rho $
. If all the relations in R are of the form
![]() $u=1$
, we say that
$u=1$
, we say that
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
is a special inverse monoid. A special inverse monoid
${\operatorname {Inv}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
is a special inverse monoid. A special inverse monoid
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{u=1} \bigr \rangle }$
with a single relator is called a one-relator inverse monoid.
${\operatorname {Inv}\bigl \langle {A}\:|\:{u=1} \bigr \rangle }$
with a single relator is called a one-relator inverse monoid.
Every inverse monoid has a (unique) maximal group homomorphic image. For the free inverse monoid
![]() $FI_A$
, this is the free group
$FI_A$
, this is the free group
![]() $F_A$
, while for a monoid
$F_A$
, while for a monoid
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
, it is the group
${\operatorname {Inv}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
, it is the group
![]() ${\operatorname {Gp}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
defined by the same presentation.
${\operatorname {Gp}\bigl \langle {A}\:|\:{R} \bigr \rangle }$
defined by the same presentation.
For a monoid (respectively, inverse monoid or group) M and a subset
![]() $X\subseteq M$
, we will denote the submonoid (respectively, inverse submonoid, subgroup) that X generates by
$X\subseteq M$
, we will denote the submonoid (respectively, inverse submonoid, subgroup) that X generates by
![]() ${\operatorname {Mon}\bigl \langle {X} \bigr \rangle }$
(respectively,
${\operatorname {Mon}\bigl \langle {X} \bigr \rangle }$
(respectively,
![]() ${\operatorname {Inv}\bigl \langle {X} \bigr \rangle }$
,
${\operatorname {Inv}\bigl \langle {X} \bigr \rangle }$
,
![]() ${\operatorname {Gp}\bigl \langle {X} \bigr \rangle }$
).
${\operatorname {Gp}\bigl \langle {X} \bigr \rangle }$
).
For a word
![]() $w \in A^{*}$
, we use
$w \in A^{*}$
, we use
![]() $\operatorname {\mathrm {pref}}(w)$
to denote the set of all prefixes of w, and
$\operatorname {\mathrm {pref}}(w)$
to denote the set of all prefixes of w, and
![]() $\operatorname {\mathrm {suff}}(w)$
to denote the set of suffixes.
$\operatorname {\mathrm {suff}}(w)$
to denote the set of suffixes.
Let
![]() $X = \{x_1, x_2, \ldots , x_n\}$
be an alphabet. We often use the notation
$X = \{x_1, x_2, \ldots , x_n\}$
be an alphabet. We often use the notation
![]() $w(x_1, \ldots , x_n)$
to denote a word from
$w(x_1, \ldots , x_n)$
to denote a word from
![]() $\overline {X}^{*}$
where we want to stress the fact that each letter of this word belongs to X or to
$\overline {X}^{*}$
where we want to stress the fact that each letter of this word belongs to X or to
![]() $X^{-1}$
. Given such a word
$X^{-1}$
. Given such a word
![]() $w(x_1, \ldots , x_n)$
and given a sequence of words
$w(x_1, \ldots , x_n)$
and given a sequence of words
![]() $p_1, \ldots , p_n$
from
$p_1, \ldots , p_n$
from
![]() $\overline {Y}^{*}$
, we use
$\overline {Y}^{*}$
, we use
![]() $w(p_1, \ldots , p_n)$
to denote the word from
$w(p_1, \ldots , p_n)$
to denote the word from
![]() $\overline {Y}^{*}$
obtained by replacing each letter
$\overline {Y}^{*}$
obtained by replacing each letter
![]() $x_i^\epsilon $
(
$x_i^\epsilon $
(
![]() $\epsilon =\pm 1$
) in the word
$\epsilon =\pm 1$
) in the word
![]() $w(x_1, \ldots , x_n)$
by the word
$w(x_1, \ldots , x_n)$
by the word
![]() $p_i^\epsilon $
.
$p_i^\epsilon $
.
The following concept is of pivotal importance for the material in this paper:
Definition 2.1. Let M be the inverse monoid defined by the presentation
A set of invertible pieces (or often we just say a set of pieces) for this presentation is a collection of words
![]() $p_1, \ldots , p_k \in \overline {A}^{*}$
which are invertible in M and satisfy
$p_1, \ldots , p_k \in \overline {A}^{*}$
which are invertible in M and satisfy
![]() ${r_i \in {\operatorname {Mon}\bigl \langle {p_1, \ldots , p_k} \bigr \rangle } \leq \overline {A}^{*}}$
for all
${r_i \in {\operatorname {Mon}\bigl \langle {p_1, \ldots , p_k} \bigr \rangle } \leq \overline {A}^{*}}$
for all
![]() $i \in \{1,2,\ldots , n\}$
. A factorisation of the relators
$i \in \{1,2,\ldots , n\}$
. A factorisation of the relators
![]() $r_i$
with respect to the pieces
$r_i$
with respect to the pieces
![]() $p_1, \ldots , p_k$
is a collection of words
$p_1, \ldots , p_k$
is a collection of words
![]() $r_i^{\prime }$
$r_i^{\prime }$
![]() $(i = 1, \ldots , n)$
over k letters, such that
$(i = 1, \ldots , n)$
over k letters, such that
For
![]() $i \in I$
by the decomposition into minimal invertible pieces, we mean the unique factorisation
$i \in I$
by the decomposition into minimal invertible pieces, we mean the unique factorisation
with the property that each
![]() $r_{i j}$
is a nonempty word in
$r_{i j}$
is a nonempty word in
![]() $\overline {A}^{*}$
which represents an invertible element of M and which has no proper nonempty invertible prefixes.
$\overline {A}^{*}$
which represents an invertible element of M and which has no proper nonempty invertible prefixes.
The following facts about cancellation in an inverse semigroup will also be used throughout the paper. They are well known and easy to prove (see [Reference Gray6, Lemma 3.1, Corollary 3.2]):
Lemma 2.2. The following hold for any inverse monoid M:
-
(i) If
 $s,x\in M$
are such that
$s,x\in M$
are such that
 $sx$
is right invertible, then
$sx$
is right invertible, then
 $sxx^{-1}=s$
.
$sxx^{-1}=s$
. -
(ii) If
 $s,t,x\in M$
are such that
$s,t,x\in M$
are such that
 $sxx^{-1}t$
is right invertible, then
$sxx^{-1}t$
is right invertible, then
 $sxx^{-1}t=st$
.
$sxx^{-1}t=st$
. -
(iii) If
 $M={\operatorname {Inv}\bigl \langle {A} \bigr \rangle }$
and
$M={\operatorname {Inv}\bigl \langle {A} \bigr \rangle }$
and
 $w\in \overline {A}^\ast $
represents a right invertible element in M, then
$w\in \overline {A}^\ast $
represents a right invertible element in M, then
 ${w=\operatorname {\mathrm {red}}(w)}$
in M.
${w=\operatorname {\mathrm {red}}(w)}$
in M.
3 Makanin-style presentation theorems for special inverse monoids
As discussed in the Introduction, given a special inverse monoid
![]() $M\kern1.2pt{=}\kern1.2pt{\operatorname {Inv}\bigl \langle {A}\:|\:{r_i\kern1.2pt{=}\kern1.2pt1\kern1pt (i\kern1.2pt{\in}\kern1.2pt I)} \bigr \rangle }$
, and decomposition of each
$M\kern1.2pt{=}\kern1.2pt{\operatorname {Inv}\bigl \langle {A}\:|\:{r_i\kern1.2pt{=}\kern1.2pt1\kern1pt (i\kern1.2pt{\in}\kern1.2pt I)} \bigr \rangle }$
, and decomposition of each
![]() $r_i$
into invertible minimal pieces, one may ask whether turning distinct pieces into distinct letters yields a presentation for the group of units of M, as it does in the monoid case. It is easy to see that this is not true in general. Consider for instance, the one-relator inverse monoid
$r_i$
into invertible minimal pieces, one may ask whether turning distinct pieces into distinct letters yields a presentation for the group of units of M, as it does in the monoid case. It is easy to see that this is not true in general. Consider for instance, the one-relator inverse monoid
We claim that the minimal invertible pieces are a,
![]() $bc^2b^{-1}$
,
$bc^2b^{-1}$
,
![]() $bc^{3}b^{-1}$
.
$bc^{3}b^{-1}$
.
To see that these three words are invertible in M, we can argue as follows. First, note that since a is both a prefix and suffix of the defining relator, it follows that a is both left and right invertible, and hence is invertible. Multiplying the defining relator on the left and right by the inverse of a then implies that
![]() $bc^2b^{-1}abc^3b^{-1}abc^2b^{-1}$
is invertible. Since this invertible word has
$bc^2b^{-1}abc^3b^{-1}abc^2b^{-1}$
is invertible. Since this invertible word has
![]() $bc^2b^{-1}$
both as a prefix and as a suffix, it follows that
$bc^2b^{-1}$
both as a prefix and as a suffix, it follows that
![]() $bc^2b^{-1}$
is invertible. Finally, multiplying on the left and right by the inverse of
$bc^2b^{-1}$
is invertible. Finally, multiplying on the left and right by the inverse of
![]() $bc^2b^{-1}$
and then the inverse of a, we deduce that
$bc^2b^{-1}$
and then the inverse of a, we deduce that
![]() $bc^3b^{-1}$
is invertible. A more general form of reasoning like this to obtain invertible pieces, called the Adjan overlap algorithm, will be discussed in Section 4. On the other hand, M is not a group, and b is not invertible, because of the homomorphism
$bc^3b^{-1}$
is invertible. A more general form of reasoning like this to obtain invertible pieces, called the Adjan overlap algorithm, will be discussed in Section 4. On the other hand, M is not a group, and b is not invertible, because of the homomorphism
![]() $M\rightarrow B$
onto the bicyclic monoid
$M\rightarrow B$
onto the bicyclic monoid
![]() $B = {\operatorname {Inv}\bigl \langle {b}\:|\:{bb^{-1}=1} \bigr \rangle }$
given by
$B = {\operatorname {Inv}\bigl \langle {b}\:|\:{bb^{-1}=1} \bigr \rangle }$
given by
![]() $a,c\mapsto 1$
,
$a,c\mapsto 1$
,
![]() $b\mapsto b$
. Since b is not invertible but
$b\mapsto b$
. Since b is not invertible but
![]() $bc^2b^{-1}$
is, it follows that
$bc^2b^{-1}$
is, it follows that
![]() $bc$
is not invertible. Similarly,
$bc$
is not invertible. Similarly,
![]() $bc^2$
and
$bc^2$
and
![]() $bc^3$
are not invertible. Therefore, a,
$bc^3$
are not invertible. Therefore, a,
![]() $bc^2b^{-1}$
,
$bc^2b^{-1}$
,
![]() $bc^{3}b^{-1}$
are indeed the minimal invertible pieces, as claimed.
$bc^{3}b^{-1}$
are indeed the minimal invertible pieces, as claimed.
Replacing these pieces by letters
![]() $x,y,z$
, respectively, yields the presentation
$x,y,z$
, respectively, yields the presentation
In the monoid M, we have
so the elements a and
![]() $t=bcb^{-1}$
form a generating set for the group of units
$t=bcb^{-1}$
form a generating set for the group of units
![]() $U=U(M)$
of M. These generators satisfy the relation
$U=U(M)$
of M. These generators satisfy the relation
![]() $xt^2xt^3xt^2x=1$
. Since U is not free with respect to
$xt^2xt^3xt^2x=1$
. Since U is not free with respect to
![]() $\{x,t\}$
and G is free of rank
$\{x,t\}$
and G is free of rank
![]() $2$
, it follows that
$2$
, it follows that
![]() $U\not \cong G$
. In fact, U is defined by the presentation
$U\not \cong G$
. In fact, U is defined by the presentation
![]() ${\operatorname {Gp}\bigl \langle {x,t}\:|\:{xt^2xt^3xt^2x=1} \bigr \rangle }$
. This will follow from the more general results we will prove below (see Corollary 3.13). A key feature of this example is that
${\operatorname {Gp}\bigl \langle {x,t}\:|\:{xt^2xt^3xt^2x=1} \bigr \rangle }$
. This will follow from the more general results we will prove below (see Corollary 3.13). A key feature of this example is that
![]() $\{a,bc^2b^{-1},bc^3b^{-1}\}$
is not a basis for
$\{a,bc^2b^{-1},bc^3b^{-1}\}$
is not a basis for
![]() ${\operatorname {Gp}\bigl \langle {a,bc^2b^{-1},bc^3b^{-1}} \bigr \rangle }\leq F_{a,b,c}$
. We now prove a result that gives an approach to studying groups of units of special inverse monoids which deals with this obstacle.
${\operatorname {Gp}\bigl \langle {a,bc^2b^{-1},bc^3b^{-1}} \bigr \rangle }\leq F_{a,b,c}$
. We now prove a result that gives an approach to studying groups of units of special inverse monoids which deals with this obstacle.
Theorem 3.1. Let
![]() $M= {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
be a special inverse monoid, let
$M= {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
be a special inverse monoid, let
![]() ${r_{i}\equiv r_{i 1}r_{i 2}\ldots r_{i k_i} }$
be a factorisation into invertible pieces for
${r_{i}\equiv r_{i 1}r_{i 2}\ldots r_{i k_i} }$
be a factorisation into invertible pieces for
![]() $i\in I$
, and let H be the subgroup of the free group
$i\in I$
, and let H be the subgroup of the free group
![]() $F_A$
generated by all the pieces
$F_A$
generated by all the pieces
![]() $r_{ij} \; ( i\in I, 1\leq j\leq k_{i} ) $
. Fix an isomorphism
$r_{ij} \; ( i\in I, 1\leq j\leq k_{i} ) $
. Fix an isomorphism
![]() $\phi :F_Y \rightarrow H$
, and set
$\phi :F_Y \rightarrow H$
, and set
If
![]() $\phi $
induces an embedding of the group
$\phi $
induces an embedding of the group
![]() $ K$
into the group
$ K$
into the group
![]() ${\operatorname {Gp}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
defined by the same presentation as M, then
${\operatorname {Gp}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
defined by the same presentation as M, then
![]() $\phi $
induces an isomorphism between K and the subgroup of the monoid M generated by the pieces.
$\phi $
induces an isomorphism between K and the subgroup of the monoid M generated by the pieces.
Proof. We begin working towards the diagram shown in Figure 1. Start from the free monoid
![]() $\overline {A}^\ast =(A\cup A^{-1})^\ast $
. The monoid
$\overline {A}^\ast =(A\cup A^{-1})^\ast $
. The monoid
![]() $M={\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
is a natural homomorphic image of it, and we denote by
$M={\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
is a natural homomorphic image of it, and we denote by
![]() $\pi _M : \overline {A}^\ast \rightarrow M$
the natural epimorphism.
$\pi _M : \overline {A}^\ast \rightarrow M$
the natural epimorphism.

Figure 1 Monoids, groups and homomorphisms in the proof of Theorem 3.1. Throughout, indexing is understood as follows:
![]() $i\in I$
,
$i\in I$
,
![]() $1\leq j\leq k_i$
,
$1\leq j\leq k_i$
,
![]() $l\in L$
.
$l\in L$
.
Let
![]() $F_A$
denote the free group on A. Recall that we regard
$F_A$
denote the free group on A. Recall that we regard
![]() $F_A$
as consisting of freely reduced words over A, and so
$F_A$
as consisting of freely reduced words over A, and so
![]() $F_A\subseteq \overline {A}^\ast $
. However, note that this inclusion is not a homomorphism. The group
$F_A\subseteq \overline {A}^\ast $
. However, note that this inclusion is not a homomorphism. The group
![]() $F_A$
is a homomorphic image of
$F_A$
is a homomorphic image of
![]() $\overline {A}^\ast $
, via the free reduction homomorphism
$\overline {A}^\ast $
, via the free reduction homomorphism
![]() $\operatorname {\mathrm {red}}:\overline {A}^\ast \rightarrow F_A$
. The group
$\operatorname {\mathrm {red}}:\overline {A}^\ast \rightarrow F_A$
. The group
![]() $G={\operatorname {Gp}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
is a natural homomorphic image of
$G={\operatorname {Gp}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
is a natural homomorphic image of
![]() $F_A$
via
$F_A$
via
![]() $\pi _G:F_A\rightarrow G$
. Since G is also an inverse monoid, and since M is defined by
$\pi _G:F_A\rightarrow G$
. Since G is also an inverse monoid, and since M is defined by
![]() $r_i=1$
,
$r_i=1$
,
![]() $i\in I$
, it follows that there exists an epimorphism
$i\in I$
, it follows that there exists an epimorphism
![]() $\psi :M\rightarrow G$
, such that
$\psi :M\rightarrow G$
, such that
Next, let
and let
As a subgroup of a free group, H itself must be free, that is
![]() $H\cong F_Y$
for some alphabet
$H\cong F_Y$
for some alphabet
![]() $Y=\{ y_l\::\: l\in L\}$
as in the statement, with an isomorphism
$Y=\{ y_l\::\: l\in L\}$
as in the statement, with an isomorphism
Since
![]() $\operatorname {\mathrm {red}}(r_{ij})\in H$
, there exist
$\operatorname {\mathrm {red}}(r_{ij})\in H$
, there exist
![]() $r_{ij}^\prime \in F_Y$
, such that
$r_{ij}^\prime \in F_Y$
, such that
Let
where
![]() $\operatorname {\mathrm {red}}_Y$
stands for the free reduction over the alphabet Y (and is not shown in the diagram). Let
$\operatorname {\mathrm {red}}_Y$
stands for the free reduction over the alphabet Y (and is not shown in the diagram). Let
with the natural epimorphism
![]() $\pi _K : F_Y\rightarrow K$
.
$\pi _K : F_Y\rightarrow K$
.
Next, we claim that the generators
![]() $\{\pi _G(s_l)\::\: l\in L\}$
of
$\{\pi _G(s_l)\::\: l\in L\}$
of
![]() $\widetilde {H}$
satisfy the relations
$\widetilde {H}$
satisfy the relations
![]() $r_i^\prime =1$
,
$r_i^\prime =1$
,
![]() $i\in I$
. Indeed
$i\in I$
. Indeed
 $$ \begin{align*} \pi_G\phi (r_i^\prime) &= \pi_G\phi \operatorname{\mathrm{red}}_Y (r_{i1}^\prime\dots r_{ik_i}^\prime) && \text{(by (4))} \\ &=\pi_G( \phi (r_{1i}^\prime)\dots \phi (r_{ik_i}^\prime)) && (\phi \text{ is a homomorphism}) \\ &=\pi_G(\operatorname{\mathrm{red}}(r_{i1})\dots\operatorname{\mathrm{red}}(r_{ik_i})) && \text{(by (3))} \\ &=\pi_G\operatorname{\mathrm{red}}(r_{i1}\dots r_{ik_i}) && (\operatorname{\mathrm{red}} \text{ is a homomorphism}) \\ &=\pi_G\operatorname{\mathrm{red}}(r)=1 .&& \end{align*} $$
$$ \begin{align*} \pi_G\phi (r_i^\prime) &= \pi_G\phi \operatorname{\mathrm{red}}_Y (r_{i1}^\prime\dots r_{ik_i}^\prime) && \text{(by (4))} \\ &=\pi_G( \phi (r_{1i}^\prime)\dots \phi (r_{ik_i}^\prime)) && (\phi \text{ is a homomorphism}) \\ &=\pi_G(\operatorname{\mathrm{red}}(r_{i1})\dots\operatorname{\mathrm{red}}(r_{ik_i})) && \text{(by (3))} \\ &=\pi_G\operatorname{\mathrm{red}}(r_{i1}\dots r_{ik_i}) && (\operatorname{\mathrm{red}} \text{ is a homomorphism}) \\ &=\pi_G\operatorname{\mathrm{red}}(r)=1 .&& \end{align*} $$
Therefore, there exists an epimorphism
To complete the set-up, we turn our attention to the subgroup U of M generated by
![]() $\{ \pi _M(r_{ij})\::\: i\in I,\ 1\leq j\leq k_i\}$
.
$\{ \pi _M(r_{ij})\::\: i\in I,\ 1\leq j\leq k_i\}$
.
We claim that
Since
![]() $s_l\in H={\operatorname {Gp}\bigl \langle {\{ \operatorname {\mathrm {red}}(r_{ij})\: :\: i\in I,\ 1\leq i\leq k_i\} } \bigr \rangle }$
, it follows that
$s_l\in H={\operatorname {Gp}\bigl \langle {\{ \operatorname {\mathrm {red}}(r_{ij})\: :\: i\in I,\ 1\leq i\leq k_i\} } \bigr \rangle }$
, it follows that
But all
![]() $\pi _M(r_{ij})$
are invertible in M by assumption, and so
$\pi _M(r_{ij})$
are invertible in M by assumption, and so
 $$ \begin{align*} U&\ni \pi_M(r_{i_1 j_1})^{\epsilon_1}\dots \pi_M(r_{i_m j_m})^{\epsilon_m} &&\\ &=\pi_M (r_{i_1 j_1}^{\epsilon_1}\dots r_{i_m}^{\epsilon_m j_m} ) && (\pi_M \text{ is a homomorphism})\\ &=\pi_M(\operatorname{\mathrm{red}}(r_{i_1 j_1}^{\epsilon_1}\dots r_{i_m j_m}^{\epsilon_m})) && \text{(by Lemma 2.2(iii))}\\ &=\pi_M(s_l), \end{align*} $$
$$ \begin{align*} U&\ni \pi_M(r_{i_1 j_1})^{\epsilon_1}\dots \pi_M(r_{i_m j_m})^{\epsilon_m} &&\\ &=\pi_M (r_{i_1 j_1}^{\epsilon_1}\dots r_{i_m}^{\epsilon_m j_m} ) && (\pi_M \text{ is a homomorphism})\\ &=\pi_M(\operatorname{\mathrm{red}}(r_{i_1 j_1}^{\epsilon_1}\dots r_{i_m j_m}^{\epsilon_m})) && \text{(by Lemma 2.2(iii))}\\ &=\pi_M(s_l), \end{align*} $$
as required.
Next, we claim that U is actually generated by
![]() $\{ \pi _M(s_l)\::\: l\in L\}$
. This is proved by a very similar argument to the one in the previous paragraph, starting from the fact that
$\{ \pi _M(s_l)\::\: l\in L\}$
. This is proved by a very similar argument to the one in the previous paragraph, starting from the fact that
![]() $\{s_l\::\: l\in L\}$
is a generating set for H, expressing the generators
$\{s_l\::\: l\in L\}$
is a generating set for H, expressing the generators
![]() $\operatorname {\mathrm {red}}(r_{ij})$
in terms of the
$\operatorname {\mathrm {red}}(r_{ij})$
in terms of the
![]() $s_l$
, and using (7). Furthermore, the generators
$s_l$
, and using (7). Furthermore, the generators
![]() $\{ \pi _M(s_l)\::\: l\in L\}$
satisfy the relations
$\{ \pi _M(s_l)\::\: l\in L\}$
satisfy the relations
![]() $r_i^\prime =1$
. Indeed
$r_i^\prime =1$
. Indeed
 $$ \begin{align*} \pi_M\phi(r_i^\prime) &= \pi_M\phi\operatorname{\mathrm{red}}_Y(r_{i1}^\prime\dots r_{ik_i}^\prime) && \text{(by (4))}\\ &= \pi_M(\phi(r_{i1}^\prime)\dots \phi(r_{ik_i}^\prime)) && (\phi \text{ is a homomorphism})\\ &=\pi_M(\operatorname{\mathrm{red}}(r_{i1})\dots \operatorname{\mathrm{red}}(r_{ik_i})) && \text{(by (3))} \\ &= \pi_M\operatorname{\mathrm{red}}(r_{i1})\dots \pi_M\operatorname{\mathrm{red}}(r_{ik_i}) && (\pi_M \text{ is a homomorphism})\\ &=\pi_M(r_{i1})\dots \pi_M(r_{ik_i}) && \text{(by Lemma 2.2(iii))} \\ &=\pi_M(r_{i1}\dots r_{ik_i}) && (\pi_M \text{ is a homomorphism}) \\ &=\pi_M(r)=1. \end{align*} $$
$$ \begin{align*} \pi_M\phi(r_i^\prime) &= \pi_M\phi\operatorname{\mathrm{red}}_Y(r_{i1}^\prime\dots r_{ik_i}^\prime) && \text{(by (4))}\\ &= \pi_M(\phi(r_{i1}^\prime)\dots \phi(r_{ik_i}^\prime)) && (\phi \text{ is a homomorphism})\\ &=\pi_M(\operatorname{\mathrm{red}}(r_{i1})\dots \operatorname{\mathrm{red}}(r_{ik_i})) && \text{(by (3))} \\ &= \pi_M\operatorname{\mathrm{red}}(r_{i1})\dots \pi_M\operatorname{\mathrm{red}}(r_{ik_i}) && (\pi_M \text{ is a homomorphism})\\ &=\pi_M(r_{i1})\dots \pi_M(r_{ik_i}) && \text{(by Lemma 2.2(iii))} \\ &=\pi_M(r_{i1}\dots r_{ik_i}) && (\pi_M \text{ is a homomorphism}) \\ &=\pi_M(r)=1. \end{align*} $$
Therefore, there exists an epimorphism
With the foregoing set-up, the assertion of our theorem can be stated as follows:
If
![]() $\zeta $
is an isomorphism between K and
$\zeta $
is an isomorphism between K and
![]() $\widetilde {H}$
, then
$\widetilde {H}$
, then
![]() $\eta $
is an isomorphism between K and U.
$\eta $
is an isomorphism between K and U.
This is now actually easy to prove: it is sufficient to show that
![]() $\eta $
and
$\eta $
and
![]() $\zeta ^{-1}\psi {\!\restriction }_U$
are mutually inverse homomorphisms. To do so, in turn, it is sufficient to verify that their two compositions act as the identity on the generating sets of U and K, respectively. Indeed, we have:
$\zeta ^{-1}\psi {\!\restriction }_U$
are mutually inverse homomorphisms. To do so, in turn, it is sufficient to verify that their two compositions act as the identity on the generating sets of U and K, respectively. Indeed, we have:
 $$ \begin{align*} \eta\zeta^{-1}\psi{\!\restriction}_U\pi_M(s_l) &= \eta\zeta^{-1}\pi_G\operatorname{\mathrm{red}} (s_l) && \text{(by (1))}\\ &=\eta\zeta^{-1}\pi_G(s_l) && (s_l \text{ is reduced}) \\ &=\eta\pi_K(y_l) && \text{(by (6))} \\ &=\pi_M(s_l) && \text{(by (8))}, \end{align*} $$
$$ \begin{align*} \eta\zeta^{-1}\psi{\!\restriction}_U\pi_M(s_l) &= \eta\zeta^{-1}\pi_G\operatorname{\mathrm{red}} (s_l) && \text{(by (1))}\\ &=\eta\zeta^{-1}\pi_G(s_l) && (s_l \text{ is reduced}) \\ &=\eta\pi_K(y_l) && \text{(by (6))} \\ &=\pi_M(s_l) && \text{(by (8))}, \end{align*} $$
and
 $$ \begin{align*} \zeta^{-1}\psi{\!\restriction}_U\eta\pi_K(y_l) &= \zeta^{-1} \psi \pi_M(s_l) && \text{(by (8))} \\ &=\zeta^{-1}\pi_G\operatorname{\mathrm{red}}(s_l) && \text{(by (1))} \\ &=\zeta^{-1}\pi_G(s_l) && (s_l \text{ is reduced}) \\ &=\pi_K(y_l) && \text{(by (6))}, \end{align*} $$
$$ \begin{align*} \zeta^{-1}\psi{\!\restriction}_U\eta\pi_K(y_l) &= \zeta^{-1} \psi \pi_M(s_l) && \text{(by (8))} \\ &=\zeta^{-1}\pi_G\operatorname{\mathrm{red}}(s_l) && \text{(by (1))} \\ &=\zeta^{-1}\pi_G(s_l) && (s_l \text{ is reduced}) \\ &=\pi_K(y_l) && \text{(by (6))}, \end{align*} $$
completing the proof of the theorem.
It is reasonable to ask whether if one translates the presentation for K given in Theorem 3.1 back into the alphabet A, the resulting presentation defines M. The following theorem shows that this indeed is the case when the pieces are reduced words.
Theorem 3.2. Let
![]() $M= {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
be a special inverse monoid, let
$M= {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
be a special inverse monoid, let
![]() ${r_{i}\equiv r_{i 1}r_{i 2}\ldots r_{i k_i} }$
be a factorisation into invertible pieces for
${r_{i}\equiv r_{i 1}r_{i 2}\ldots r_{i k_i} }$
be a factorisation into invertible pieces for
![]() $i\in I$
and suppose that all pieces are reduced words. Let
$i\in I$
and suppose that all pieces are reduced words. Let
![]() $\phi $
be an epimorphism from some free group
$\phi $
be an epimorphism from some free group
![]() $F_Y$
onto the subgroup of
$F_Y$
onto the subgroup of
![]() $F_A$
generated by the pieces, and for every piece
$F_A$
generated by the pieces, and for every piece
![]() $r_{ij}$
, pick a preimage
$r_{ij}$
, pick a preimage
![]() $r_{ij}^\prime \in F_Y$
under
$r_{ij}^\prime \in F_Y$
under
![]() $\phi $
. Finally, let
$\phi $
. Finally, let
![]() $\pi :\overline {Y}^{*} \rightarrow \overline {A}^{*}$
be the homomorphism extending
$\pi :\overline {Y}^{*} \rightarrow \overline {A}^{*}$
be the homomorphism extending
![]() $x \mapsto \phi (x)$
$x \mapsto \phi (x)$
![]() $(x \in \overline {X})$
. Then
$(x \in \overline {X})$
. Then
and
![]() $\{ \pi (y): y \in \overline {Y} \}$
is a set of invertible pieces for
$\{ \pi (y): y \in \overline {Y} \}$
is a set of invertible pieces for
![]() ${\operatorname {Inv}\bigl \langle {A }\:|\:{\pi (r_{i 1}^\prime ) \ldots \pi (r_{i k_i}^\prime )=1 \; (i \in I)} \bigr \rangle }$
which generates the same subgroup of M as the original pieces
${\operatorname {Inv}\bigl \langle {A }\:|\:{\pi (r_{i 1}^\prime ) \ldots \pi (r_{i k_i}^\prime )=1 \; (i \in I)} \bigr \rangle }$
which generates the same subgroup of M as the original pieces
![]() $\{ r_{i j} \::\: i \in I,\ 1 \leq j \leq k_i\}$
.
$\{ r_{i j} \::\: i \in I,\ 1 \leq j \leq k_i\}$
.
Proof. Denoting by
![]() $\operatorname {\mathrm {red}}_A$
the free reduction over the alphabet A, we have
$\operatorname {\mathrm {red}}_A$
the free reduction over the alphabet A, we have
and, in particular,
because all
![]() $r_{ij}$
are reduced.
$r_{ij}$
are reduced.
Now, we show that all the relations
![]() $\pi (r_{i 1}^\prime ) \ldots \pi (r_{i k_i}^\prime )=1$
hold in the monoid M. Indeed, denoting by
$\pi (r_{i 1}^\prime ) \ldots \pi (r_{i k_i}^\prime )=1$
hold in the monoid M. Indeed, denoting by
![]() $\pi _M:\overline {A}^\ast \rightarrow M$
the natural epimorphism, we have
$\pi _M:\overline {A}^\ast \rightarrow M$
the natural epimorphism, we have
 $$ \begin{align*} \pi_M(\pi(r_{i1}^\prime)\dots \pi(r_{ik_i}^\prime)) &= \pi_M(\operatorname{\mathrm{red}}_A\pi(r_{i1}^\prime)\dots \operatorname{\mathrm{red}}_A\pi(r_{ik_i}^\prime)) && \text{(by Lemma 2.2(iii))}\\ &=\pi_M(r_{i1}\dots r_{ik_i}) && \text{(by (10))}\\ &=\pi_M(r_i)=1_M.&& \end{align*} $$
$$ \begin{align*} \pi_M(\pi(r_{i1}^\prime)\dots \pi(r_{ik_i}^\prime)) &= \pi_M(\operatorname{\mathrm{red}}_A\pi(r_{i1}^\prime)\dots \operatorname{\mathrm{red}}_A\pi(r_{ik_i}^\prime)) && \text{(by Lemma 2.2(iii))}\\ &=\pi_M(r_{i1}\dots r_{ik_i}) && \text{(by (10))}\\ &=\pi_M(r_i)=1_M.&& \end{align*} $$
Furthermore, these relations imply the original ones. To see this, let
![]() $M^\prime $
be the monoid defined by
$M^\prime $
be the monoid defined by
![]() ${\operatorname {Inv}\bigl \langle {A }\:|\:{\pi (r_{i 1}^\prime ) \ldots \pi (r_{i k_i}^\prime )=1 \; (i \in I)} \bigr \rangle }$
, and let
${\operatorname {Inv}\bigl \langle {A }\:|\:{\pi (r_{i 1}^\prime ) \ldots \pi (r_{i k_i}^\prime )=1 \; (i \in I)} \bigr \rangle }$
, and let
![]() $\pi _{M^\prime }:\overline {A}^\ast \rightarrow M^\prime $
be the associated natural epimorphism, and then
$\pi _{M^\prime }:\overline {A}^\ast \rightarrow M^\prime $
be the associated natural epimorphism, and then
 $$ \begin{align*} 1_{M^\prime} &= \pi_{M^\prime} (\pi(r_{i1}^\prime)\dots\pi(r_{ik_i}^\prime)) &&\\ &=\pi_{M^\prime}(\operatorname{\mathrm{red}}_A\pi(r_{i1}^\prime)\dots\operatorname{\mathrm{red}}_A\pi(r_{ik_i}^\prime)) && \text{(by Lemma 2.2(iii))} \\ &=\pi_{M^\prime}(r_{i1}\dots r_{ik_i}) && \text{(by (10))} \\ &=\pi_{M^\prime}(r_i). && \end{align*} $$
$$ \begin{align*} 1_{M^\prime} &= \pi_{M^\prime} (\pi(r_{i1}^\prime)\dots\pi(r_{ik_i}^\prime)) &&\\ &=\pi_{M^\prime}(\operatorname{\mathrm{red}}_A\pi(r_{i1}^\prime)\dots\operatorname{\mathrm{red}}_A\pi(r_{ik_i}^\prime)) && \text{(by Lemma 2.2(iii))} \\ &=\pi_{M^\prime}(r_{i1}\dots r_{ik_i}) && \text{(by (10))} \\ &=\pi_{M^\prime}(r_i). && \end{align*} $$
This proves (9).
To prove that each
![]() $\pi (y)$
is invertible in M, note that by the assumptions of the theorem,
$\pi (y)$
is invertible in M, note that by the assumptions of the theorem,
![]() $\phi (y)$
belongs to the subgroup of the free group
$\phi (y)$
belongs to the subgroup of the free group
![]() $F_A$
generated by
$F_A$
generated by
![]() $\{ r_{ij}\::\: i\in I,\ 1\leq j\leq k_i\}$
, and that
$\{ r_{ij}\::\: i\in I,\ 1\leq j\leq k_i\}$
, and that
![]() $\pi (y)\equiv \phi (y)$
. Hence, we can write
$\pi (y)\equiv \phi (y)$
. Hence, we can write
Since all
![]() $r_{ij}$
are units in M, by Lemma 2.2(iii), we have
$r_{ij}$
are units in M, by Lemma 2.2(iii), we have
Combining (11) and (12), we obtain:
which is clearly a unit.
Finally, since each relator
![]() $\pi (r_{i 1}^\prime ) \ldots \pi (r_{i k_i}^\prime )$
is clearly a product of the
$\pi (r_{i 1}^\prime ) \ldots \pi (r_{i k_i}^\prime )$
is clearly a product of the
![]() $\pi (y)$
, it follows that
$\pi (y)$
, it follows that
![]() $\{ \pi (y)\::\: y\in \overline {Y}\}$
is indeed a set of pieces for the presentation
$\{ \pi (y)\::\: y\in \overline {Y}\}$
is indeed a set of pieces for the presentation
![]() ${\operatorname {Inv}\bigl \langle {A }\:|\:{\pi (r_{i 1}^\prime ) \ldots \pi (r_{i k_i}^\prime )=1 \; (i \in I)} \bigr \rangle }$
.
${\operatorname {Inv}\bigl \langle {A }\:|\:{\pi (r_{i 1}^\prime ) \ldots \pi (r_{i k_i}^\prime )=1 \; (i \in I)} \bigr \rangle }$
.
Remark 3.3. Both Theorems 3.1 and 3.2 of course apply when the pieces
![]() $r_{ij}$
are minimal. In that case, the subgroup U generated by them is the group of units of M by Theorem 1.3.
$r_{ij}$
are minimal. In that case, the subgroup U generated by them is the group of units of M by Theorem 1.3.
Remark 3.4. In the statement of Theorem 3.2, some
![]() $\pi (y)$
may actually not occur in
$\pi (y)$
may actually not occur in
![]() $\pi (r_{i 1}^\prime ) \ldots \pi (r_{i k_i}^\prime )$
. Also, we note that the assumptions in Theorem 3.2 can be weakened a little further: instead of the original pieces being reduced, one could require that
$\pi (r_{i 1}^\prime ) \ldots \pi (r_{i k_i}^\prime )$
. Also, we note that the assumptions in Theorem 3.2 can be weakened a little further: instead of the original pieces being reduced, one could require that
![]() $r_{ij}$
can be obtained from
$r_{ij}$
can be obtained from
![]() $\pi (r_{ij}^\prime )$
by using reductions.
$\pi (r_{ij}^\prime )$
by using reductions.
Remark 3.5. The statement of Theorem 3.2 is technical. When Theorem 3.2 is applied in the particular case where the factorizations of the defining relators are all into minimal invertible pieces, then, expressed in a slightly less technical way, this theorem tells us that given
![]() $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
, then for any basis
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
, then for any basis
![]() $B \subseteq F_A$
of the subgroup of
$B \subseteq F_A$
of the subgroup of
![]() $F_A$
generated by the minimal invertible pieces of the relators of this presentation, there is a presentation
$F_A$
generated by the minimal invertible pieces of the relators of this presentation, there is a presentation
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{s_i=1 \; (i \in I)} \bigr \rangle }$
for M for which B is a set of invertible pieces and also generates the group of units of M. As we shall see below, changing the presentation for M in this way will often be a useful first step when analysing examples.
${\operatorname {Inv}\bigl \langle {A}\:|\:{s_i=1 \; (i \in I)} \bigr \rangle }$
for M for which B is a set of invertible pieces and also generates the group of units of M. As we shall see below, changing the presentation for M in this way will often be a useful first step when analysing examples.
We note that the assumption that the pieces are reduced is necessary in Theorem 3.2. Indeed, in the monoid
![]() ${\operatorname {Inv}\bigl \langle {x,y}\:|\:{xx^{-1}yy^{-1}xx^{-1}=1} \bigr \rangle }$
, the minimal invertible pieces are
${\operatorname {Inv}\bigl \langle {x,y}\:|\:{xx^{-1}yy^{-1}xx^{-1}=1} \bigr \rangle }$
, the minimal invertible pieces are
![]() $xx^{-1}$
and
$xx^{-1}$
and
![]() $yy^{-1}$
. In
$yy^{-1}$
. In
![]() $F_{x,y}$
, they generate the trivial subgroup. However, the original monoid is not isomorphic to the free inverse monoid
$F_{x,y}$
, they generate the trivial subgroup. However, the original monoid is not isomorphic to the free inverse monoid
![]() ${\operatorname {Inv}\bigl \langle {x,y}\:|\: \bigr \rangle }$
.
${\operatorname {Inv}\bigl \langle {x,y}\:|\: \bigr \rangle }$
.
Motivated by Theorem 3.1, we introduce the following concept:
Definition 3.6. A finite set of words
![]() $w_1, \ldots , w_k \in \overline {A}^{*}$
is free for substitution in a group presentation
$w_1, \ldots , w_k \in \overline {A}^{*}$
is free for substitution in a group presentation
if the subgroup of
generated by
![]() $w_1, \ldots , w_k$
is isomorphic to
$w_1, \ldots , w_k$
is isomorphic to
![]() ${\operatorname {Gp}\bigl \langle {x_1,\dots ,x_k}\:|\:{r_i(x_1, \ldots , x_k) = 1\ (i\in I)} \bigr \rangle }$
via the map
${\operatorname {Gp}\bigl \langle {x_1,\dots ,x_k}\:|\:{r_i(x_1, \ldots , x_k) = 1\ (i\in I)} \bigr \rangle }$
via the map
![]() $x_i \mapsto w_i$
.
$x_i \mapsto w_i$
.
Corollary 3.7. Let A be an alphabet, and suppose that
![]() $r_1,\dots , r_k\in \overline {A}^\ast $
are such that the free group
$r_1,\dots , r_k\in \overline {A}^\ast $
are such that the free group
![]() $H={\operatorname {Gp}\bigl \langle {r_1,\dots ,r_k} \bigr \rangle }\leq F_A$
has a basis which is free for substitution into any one-relator presentation. Then the group U of units of any one-relator inverse monoid
$H={\operatorname {Gp}\bigl \langle {r_1,\dots ,r_k} \bigr \rangle }\leq F_A$
has a basis which is free for substitution into any one-relator presentation. Then the group U of units of any one-relator inverse monoid
![]() ${M={\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }}$
, where the minimal invertible pieces of r are precisely
${M={\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }}$
, where the minimal invertible pieces of r are precisely
![]() $ r_1,\dots , r_k$
, is again a one-relator group. Specifically, if
$ r_1,\dots , r_k$
, is again a one-relator group. Specifically, if
![]() $\{ p_1,\dots , p_n\}$
is a basis for H, if each
$\{ p_1,\dots , p_n\}$
is a basis for H, if each
![]() $r_j$
is expressed in terms of this basis as
$r_j$
is expressed in terms of this basis as
![]() $r_j=r_j^\prime (p_1,\dots ,p_n)$
, where
$r_j=r_j^\prime (p_1,\dots ,p_n)$
, where
![]() $r_j^\prime \in \overline {\{x_1,\dots ,x_n\}}^\ast $
, and if
$r_j^\prime \in \overline {\{x_1,\dots ,x_n\}}^\ast $
, and if
![]() $r=r^\prime (r_1,\dots , r_k)$
, then U is defined by
$r=r^\prime (r_1,\dots , r_k)$
, then U is defined by
It is therefore of interest to investigate sets that are free for substitutions into one-relator presentations, or indeed, into arbitrary presentations. For instance, we can prove the following:
Theorem 3.8. Let A be an alphabet, let
![]() $p_1, \ldots , p_n \in F_A$
and denote by
$p_1, \ldots , p_n \in F_A$
and denote by
![]() $A_i$
the set of letters of A that occur in
$A_i$
the set of letters of A that occur in
![]() $p_i$
. If
$p_i$
. If
then
![]() $\{p_1,\dots , p_n\}$
is free for substitutions into any one-relator presentation.
$\{p_1,\dots , p_n\}$
is free for substitutions into any one-relator presentation.
The following two lemmas will be used in the proof:
Lemma 3.9. If
![]() $G = {\operatorname {Gp}\bigl \langle {A}\:|\:{r_1=1, r_2=1} \bigr \rangle }$
, where each
$G = {\operatorname {Gp}\bigl \langle {A}\:|\:{r_1=1, r_2=1} \bigr \rangle }$
, where each
![]() $r_i$
is cyclically reduced and contains a letter
$r_i$
is cyclically reduced and contains a letter
![]() $a_i$
not contained by the other
$a_i$
not contained by the other
![]() $r_j$
, then the one-relator groups
$r_j$
, then the one-relator groups
![]() ${G_1={\operatorname {Gp}\bigl \langle {A \setminus \{a_2\}}\:|\:{r_1=1} \bigr \rangle }}$
and
${G_1={\operatorname {Gp}\bigl \langle {A \setminus \{a_2\}}\:|\:{r_1=1} \bigr \rangle }}$
and
![]() $G_2={\operatorname {Gp}\bigl \langle {A \setminus \{a_1\}}\:|\:{r_2=1} \bigr \rangle }$
both embed naturally into G.
$G_2={\operatorname {Gp}\bigl \langle {A \setminus \{a_1\}}\:|\:{r_2=1} \bigr \rangle }$
both embed naturally into G.
Proof. The subgroup of
![]() $G_1$
generated by
$G_1$
generated by
![]() $A\setminus \{ a_1,a_2\}$
is free on that set by Freiheitsatz [Reference Magnus, Karrass and Solitar19, Theorem 4.10], since the letter
$A\setminus \{ a_1,a_2\}$
is free on that set by Freiheitsatz [Reference Magnus, Karrass and Solitar19, Theorem 4.10], since the letter
![]() $a_1$
occurs in
$a_1$
occurs in
![]() $r_1$
. Likewise, writing
$r_1$
. Likewise, writing
![]() $G_2={\operatorname {Gp}\bigl \langle {A^\prime \setminus \{a_1^\prime \}}\:|\:{r_2^\prime =1} \bigr \rangle }$
over a disjoint copy of A, the subgroup generated by
$G_2={\operatorname {Gp}\bigl \langle {A^\prime \setminus \{a_1^\prime \}}\:|\:{r_2^\prime =1} \bigr \rangle }$
over a disjoint copy of A, the subgroup generated by
![]() $A^\prime \setminus \{a_1^\prime ,a_2^\prime \}$
is free. So we can form the free product with amalgamation
$A^\prime \setminus \{a_1^\prime ,a_2^\prime \}$
is free. So we can form the free product with amalgamation
into which
![]() $G_1$
and
$G_1$
and
![]() $G_2$
will embed naturally. Now perform Tietze transformations [Reference Magnus, Karrass and Solitar19, Section 1.5] to remove the generators
$G_2$
will embed naturally. Now perform Tietze transformations [Reference Magnus, Karrass and Solitar19, Section 1.5] to remove the generators
![]() $a^\prime $
with
$a^\prime $
with
![]() $a\in A\setminus \{a_1,a_2\}$
, rename
$a\in A\setminus \{a_1,a_2\}$
, rename
![]() $a_2^\prime $
into
$a_2^\prime $
into
![]() $a_2$
and we obtain
$a_2$
and we obtain
![]() ${\operatorname {Gp}\bigl \langle {A}\:|\:{r_1=1,\ r_2=1} \bigr \rangle }=G$
.
${\operatorname {Gp}\bigl \langle {A}\:|\:{r_1=1,\ r_2=1} \bigr \rangle }=G$
.
Lemma 3.10. Let A and
![]() $X = \{ x_1, \ldots , x_n \}$
be two alphabets, and let
$X = \{ x_1, \ldots , x_n \}$
be two alphabets, and let
![]() $r = r(x_1, \ldots , x_n) \in F_X$
be a cyclically reduced word in which all of the letters
$r = r(x_1, \ldots , x_n) \in F_X$
be a cyclically reduced word in which all of the letters
![]() $x_1, \ldots , x_n$
appear. Further, let
$x_1, \ldots , x_n$
appear. Further, let
![]() $p_1, \ldots , p_n \in F_A$
, and denote by
$p_1, \ldots , p_n \in F_A$
, and denote by
![]() $A_i$
the set of letters of A that appear in
$A_i$
the set of letters of A that appear in
![]() $p_i$
. Suppose that
$p_i$
. Suppose that
with
![]() $a_i\in A_i \setminus \bigcup _{j \neq i}{A_j}$
. Then each of the letters
$a_i\in A_i \setminus \bigcup _{j \neq i}{A_j}$
. Then each of the letters
![]() $a_i$
$a_i$
![]() $(i = 1, \ldots , n)$
appears in any cyclic reduction of the word
$(i = 1, \ldots , n)$
appears in any cyclic reduction of the word
![]() $r(p_1, \ldots , p_n)$
.
$r(p_1, \ldots , p_n)$
.
Proof. Since r is cyclically reduced, and since we are concerned with cyclically reduced forms of
![]() $r(p_1,\dots ,p_n)$
, we may without loss of generality assume that r has the form
$r(p_1,\dots ,p_n)$
, we may without loss of generality assume that r has the form
where
![]() $ i_j\in \{1,\dots ,n\}$
and
$ i_j\in \{1,\dots ,n\}$
and
![]() $ \alpha _j\in \mathbb {Z}$
for
$ \alpha _j\in \mathbb {Z}$
for
![]() $ j=1,\dots , k$
, and
$ j=1,\dots , k$
, and
Consider the word
and inside it, for every
![]() $j=1,\dots , k$
, consider all the occurrences of the letter
$j=1,\dots , k$
, consider all the occurrences of the letter
![]() $a_{i_j}$
appearing in the reduced word
$a_{i_j}$
appearing in the reduced word
![]() $\operatorname {\mathrm {red}}(p_{i_j}^{\alpha _j})$
. Notice that there must be at least one such occurrence, since
$\operatorname {\mathrm {red}}(p_{i_j}^{\alpha _j})$
. Notice that there must be at least one such occurrence, since
![]() $p_{i_j}$
is reduced, and hence, the set of letters appearing in
$p_{i_j}$
is reduced, and hence, the set of letters appearing in
![]() $p_{i_j}$
is the same as the set of letters appearing in
$p_{i_j}$
is the same as the set of letters appearing in
![]() $\operatorname {\mathrm {red}}(p_{i_j}^{\alpha _j})$
. We claim that none of these occurrences are cancelled in the process of free reduction of
$\operatorname {\mathrm {red}}(p_{i_j}^{\alpha _j})$
. We claim that none of these occurrences are cancelled in the process of free reduction of
![]() $r(p_1,\dots , p_n)$
.
$r(p_1,\dots , p_n)$
.
To see this, suppose, to the contrary, that two occurrences of some
![]() $a_i$
cancel each other. Let those two occurrences appear in
$a_i$
cancel each other. Let those two occurrences appear in
![]() $p_{i_l}^{\alpha _l}$
and
$p_{i_l}^{\alpha _l}$
and
![]() $p_{i_m}^{\alpha _m}$
, where
$p_{i_m}^{\alpha _m}$
, where
![]() $i=i_l=i_m$
and
$i=i_l=i_m$
and
![]() $l\leq m$
. Furthermore, choose i, l and m so that
$l\leq m$
. Furthermore, choose i, l and m so that
![]() $m-l$
is as small as possible. By assumption, the occurrence of
$m-l$
is as small as possible. By assumption, the occurrence of
![]() $a_i$
in
$a_i$
in
![]() $p_{i_l}$
is not cancelled when reducing to
$p_{i_l}$
is not cancelled when reducing to
![]() $\operatorname {\mathrm {red}}(p_{i_l}^{\alpha _l})$
, and hence, we cannot have
$\operatorname {\mathrm {red}}(p_{i_l}^{\alpha _l})$
, and hence, we cannot have
![]() $m=l$
. Also, since
$m=l$
. Also, since
![]() $i_{l+1}\neq i_l$
, the word
$i_{l+1}\neq i_l$
, the word
![]() $p_{i_{l+1}}$
contains no occurrences of
$p_{i_{l+1}}$
contains no occurrences of
![]() $a_i=a_{i_l}$
, and so
$a_i=a_{i_l}$
, and so
![]() $m\neq l+1$
. Therefore, we must have
$m\neq l+1$
. Therefore, we must have
![]() $m\geq l+2$
. But now, in order for the two occurrences of
$m\geq l+2$
. But now, in order for the two occurrences of
![]() $a_i$
in
$a_i$
in
![]() $p_{i_l}^{\alpha _l}$
and
$p_{i_l}^{\alpha _l}$
and
![]() $p_{i_m}^{\alpha _m}$
to cancel each other, any occurrence of
$p_{i_m}^{\alpha _m}$
to cancel each other, any occurrence of
![]() $a_{i_{l+1}}$
in
$a_{i_{l+1}}$
in
![]() $p_{i_{l+1}}^{\alpha _{l+1}}$
must also be cancelled. Since there are no occurrences of
$p_{i_{l+1}}^{\alpha _{l+1}}$
must also be cancelled. Since there are no occurrences of
![]() $a_{i_{l+1}}$
in
$a_{i_{l+1}}$
in
![]() $p_{i_l}^{\alpha _l}$
, it follows that these occurrences must cancel within
$p_{i_l}^{\alpha _l}$
, it follows that these occurrences must cancel within
![]() $p_{i_{l+1}}^{\alpha _{l+1}}\dots p_{i_m}^{\alpha _m}$
, and this contradicts the minimality of
$p_{i_{l+1}}^{\alpha _{l+1}}\dots p_{i_m}^{\alpha _m}$
, and this contradicts the minimality of
![]() $m-l$
. This proves the claim that no two occurrences of some
$m-l$
. This proves the claim that no two occurrences of some
![]() $a_i$
within some
$a_i$
within some
![]() $p_{i_l}^{\alpha _l}$
and
$p_{i_l}^{\alpha _l}$
and
![]() $p_{i_m}^{\alpha _m}$
(
$p_{i_m}^{\alpha _m}$
(
![]() $i_l=i_m=i$
) cancel each other in the process of free reduction of
$i_l=i_m=i$
) cancel each other in the process of free reduction of
![]() $r(p_1,\dots ,p_n)$
.
$r(p_1,\dots ,p_n)$
.
Now suppose that a cancellation of some
![]() $a_{i_l}$
appearing in some
$a_{i_l}$
appearing in some
![]() $p_{i_l}^{\alpha _l}$
can happen during the cyclic reduction of
$p_{i_l}^{\alpha _l}$
can happen during the cyclic reduction of
![]() $r(p_1,\dots ,p_n)$
. Then this occurrence of
$r(p_1,\dots ,p_n)$
. Then this occurrence of
![]() $a_{i_l}$
would be cancelled during the free reduction of at least one of the words
$a_{i_l}$
would be cancelled during the free reduction of at least one of the words
However, the words
satisfy the original assumptions made about r, and hence, such cancellation cannot take place by the argument from the previous paragraph. This completes the proof of the lemma.
Proof of Theorem 3.8
Let
![]() $X=\{ x_1,\dots , x_n\}$
. Suppose
$X=\{ x_1,\dots , x_n\}$
. Suppose
![]() $p_1,\dots , p_n\in \overline {A}^\ast $
, and let
$p_1,\dots , p_n\in \overline {A}^\ast $
, and let
![]() $A_i$
be the set of letters appearing in
$A_i$
be the set of letters appearing in
![]() $p_i$
. For every
$p_i$
. For every
![]() $i=1,\dots , n$
, pick
$i=1,\dots , n$
, pick
![]() $a_i\in A_i\setminus \bigcup _{j\neq i} A_j$
. We need to show that for every
$a_i\in A_i\setminus \bigcup _{j\neq i} A_j$
. We need to show that for every
![]() $r\in \overline {X}^\ast $
, the subgroup of
$r\in \overline {X}^\ast $
, the subgroup of
generated by
![]() $p_1,\dots , p_n$
is naturally isomorphic to
$p_1,\dots , p_n$
is naturally isomorphic to
![]() ${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
. Clearly, we may assume without loss of generality that r is cyclically reduced. We will prove the assertion by induction on the length of the word
${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
. Clearly, we may assume without loss of generality that r is cyclically reduced. We will prove the assertion by induction on the length of the word
![]() $r(p_1,\dots ,p_n)$
. If
$r(p_1,\dots ,p_n)$
. If
![]() $|r(p_1,\dots ,p_n)|=0$
, Lemma 3.10 gives
$|r(p_1,\dots ,p_n)|=0$
, Lemma 3.10 gives
![]() $|r|=0$
, and the assertion is obvious. It is also obvious when
$|r|=0$
, and the assertion is obvious. It is also obvious when
![]() $|p_i|=1$
for all
$|p_i|=1$
for all
![]() $i=1,\dots ,n$
. So, suppose that some
$i=1,\dots ,n$
. So, suppose that some
![]() $p_i$
has length greater than
$p_i$
has length greater than
![]() $1$
. Without loss, we may assume
$1$
. Without loss, we may assume
![]() $|p_n|>1$
. In the presentation (13) for G, introduce a new generator
$|p_n|>1$
. In the presentation (13) for G, introduce a new generator
![]() $x_n$
satisfying
$x_n$
satisfying
![]() $x_n=p_n$
, to obtain:
$x_n=p_n$
, to obtain:
where
![]() $\overline {r}$
denotes a cyclically reduced form of
$\overline {r}$
denotes a cyclically reduced form of
![]() $r(p_1,\dots ,p_{n-1},x_n)$
. We claim that presentation (15) satisfies the assumptions of Lemma 3.9. Indeed:
$r(p_1,\dots ,p_{n-1},x_n)$
. We claim that presentation (15) satisfies the assumptions of Lemma 3.9. Indeed:
-
• The word
 $p_nx_n^{-1}$
is cyclically reduced because
$p_nx_n^{-1}$
is cyclically reduced because
 $p_n$
is a reduced word over
$p_n$
is a reduced word over
 $\overline {A}$
and
$\overline {A}$
and
 $x_n\not \in \overline {A}$
.
$x_n\not \in \overline {A}$
. -
• The word
 $\overline {r}$
is cyclically reduced by assumption.
$\overline {r}$
is cyclically reduced by assumption. -
• The letter
 $a_n$
appears in
$a_n$
appears in
 $p_n$
and in none of
$p_n$
and in none of
 $p_1,\dots ,p_{n-1}$
; hence,
$p_1,\dots ,p_{n-1}$
; hence,
 $a_n$
will appear in
$a_n$
will appear in
 $p_nx_n^{-1}$
but not in
$p_nx_n^{-1}$
but not in
 $r(p_1,\dots ,p_{n-1},x_n)$
, and hence, not in
$r(p_1,\dots ,p_{n-1},x_n)$
, and hence, not in
 $\overline {r}$
either.
$\overline {r}$
either. -
• The letter
 $a_1$
appears in
$a_1$
appears in
 $p_1$
, but not in any other
$p_1$
, but not in any other
 $p_2,\dots ,p_n$
; hence, it will appear in
$p_2,\dots ,p_n$
; hence, it will appear in
 $r(p_1,\dots ,p_{n-1},x_n)$
by Lemma 3.10, but not in
$r(p_1,\dots ,p_{n-1},x_n)$
by Lemma 3.10, but not in
 $p_nx_n^{-1}$
.
$p_nx_n^{-1}$
.
By Lemma 3.9, the group
embeds naturally into G, as defined by (15). Note that
![]() $|r(p_1,\dots ,p_{n-1},x_n)|<|r(p_1,\dots ,p_n)|$
because
$|r(p_1,\dots ,p_{n-1},x_n)|<|r(p_1,\dots ,p_n)|$
because
![]() $|p_n|\geq 2$
. Furthermore, note that the words
$|p_n|\geq 2$
. Furthermore, note that the words
![]() $p_1,\dots ,p_{n-1},x_n$
satisfy all the original assumptions about
$p_1,\dots ,p_{n-1},x_n$
satisfy all the original assumptions about
![]() $p_1,\dots , p_n$
– they are reduced, and each contains a letter not appearing in any of the others. Therefore, the inductive hypothesis applies, and the subgroup of the group (16) generated by
$p_1,\dots , p_n$
– they are reduced, and each contains a letter not appearing in any of the others. Therefore, the inductive hypothesis applies, and the subgroup of the group (16) generated by
![]() $p_1,\dots , p_{n-1},x_n$
is naturally isomorphic to
$p_1,\dots , p_{n-1},x_n$
is naturally isomorphic to
![]() ${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
. But, inside G, this subgroup coincides with the subgroup generated by
${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
. But, inside G, this subgroup coincides with the subgroup generated by
![]() $p_1,\dots ,p_n$
, and the theorem is proved.
$p_1,\dots ,p_n$
, and the theorem is proved.
We can generalise the above condition a bit further:
Theorem 3.11. Let
![]() $A=B\cup C$
, where B and C are disjoint alphabets, and let
$A=B\cup C$
, where B and C are disjoint alphabets, and let
![]() $p_1,\dots ,p_n\subseteq F_A$
. Denoting by
$p_1,\dots ,p_n\subseteq F_A$
. Denoting by
![]() $c(p_i)$
the set of letters from C that appear in
$c(p_i)$
the set of letters from C that appear in
![]() $p_i$
, suppose that there is a bijection
$p_i$
, suppose that there is a bijection
![]() $\mu : \{p_1,\dots ,p_n\}\rightarrow C$
, such that at least one of the following two conditions holds for every
$\mu : \{p_1,\dots ,p_n\}\rightarrow C$
, such that at least one of the following two conditions holds for every
![]() $i=1,\dots , n$
:
$i=1,\dots , n$
:
-
(i)
 $c(p_i) = \{ \mu (p_i) \}$
; or
$c(p_i) = \{ \mu (p_i) \}$
; or -
(ii)
 $\mu (p_i)$
occurs precisely once in
$\mu (p_i)$
occurs precisely once in
 $p_i$
and
$p_i$
and  $$\begin{align*}c(p_i) \setminus \bigcup_{1 \leq j \leq i-1}c(p_j) = \{ \mu(p_i) \}. \end{align*}$$
$$\begin{align*}c(p_i) \setminus \bigcup_{1 \leq j \leq i-1}c(p_j) = \{ \mu(p_i) \}. \end{align*}$$
Then
![]() $p_1,\dots , p_m$
are free for substitutions into arbitrary one-relator presentations.
$p_1,\dots , p_m$
are free for substitutions into arbitrary one-relator presentations.
Remark 3.12. Theorem 3.8 is indeed a special case of Theorem 3.11, corresponding to the case where Condition (i) is satisfied for every
![]() $i=1,\dots ,n$
.
$i=1,\dots ,n$
.
Proof. We may reorder
![]() $p_1,\dots , p_n$
so that
$p_1,\dots , p_n$
so that
![]() $p_1,\dots , p_m$
satisfy Condition (i) and
$p_1,\dots , p_m$
satisfy Condition (i) and
![]() $p_{m+1},\dots p_n$
satisfy Condition (ii) for some
$p_{m+1},\dots p_n$
satisfy Condition (ii) for some
![]() $1\leq m\leq n$
. For
$1\leq m\leq n$
. For
![]() $i=1,\dots ,n$
, let
$i=1,\dots ,n$
, let
![]() $c_i=\mu (p_i)$
so that
$c_i=\mu (p_i)$
so that
![]() ${C=\{c_1,\dots ,c_n\}}$
, and let
${C=\{c_1,\dots ,c_n\}}$
, and let
![]() $x_1,\dots , x_n,d_{m+1},\dots , d_n$
be new letters, not in A.
$x_1,\dots , x_n,d_{m+1},\dots , d_n$
be new letters, not in A.
We need to prove that for every word
![]() $r=r(x_1,\dots ,x_n)$
over
$r=r(x_1,\dots ,x_n)$
over
![]() $\overline {\{x_1,\dots ,x_n\}}$
, the subgroup of
$\overline {\{x_1,\dots ,x_n\}}$
, the subgroup of
generated by
![]() $p_1,\dots ,p_n$
is naturally isomorphic to
$p_1,\dots ,p_n$
is naturally isomorphic to
![]() ${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
, where
${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
, where
![]() $X = \{x_1, \ldots , x_n \}$
. To begin with, by Theorem 3.8, the subgroup of
$X = \{x_1, \ldots , x_n \}$
. To begin with, by Theorem 3.8, the subgroup of
generated by
![]() $p_1,\dots ,p_m,d_{m+1},\dots , d_n$
is naturally isomorphic to
$p_1,\dots ,p_m,d_{m+1},\dots , d_n$
is naturally isomorphic to
![]() ${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
. We treat this as the inductive anchor for the claim that for every
${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
. We treat this as the inductive anchor for the claim that for every
![]() $k=0,\dots , n-m$
, the subgroup of
$k=0,\dots , n-m$
, the subgroup of
generated by
![]() $p_1,\dots ,p_{m+k},d_{m+k+1},\dots , d_n$
is naturally isomorphic to
$p_1,\dots ,p_{m+k},d_{m+k+1},\dots , d_n$
is naturally isomorphic to
![]() ${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
. Suppose the claim is true for some k, and we prove it for
${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
. Suppose the claim is true for some k, and we prove it for
![]() $k+1$
. First, we write
$k+1$
. First, we write
![]() $p_{m+k+1}\equiv qc_{m+k+1}r$
, where
$p_{m+k+1}\equiv qc_{m+k+1}r$
, where
![]() $q,r\in \overline {B\cup \{c_1,\dots , c_{m+k}\}}^\ast $
, because of Condition (ii). Then, we introduce a new generator
$q,r\in \overline {B\cup \{c_1,\dots , c_{m+k}\}}^\ast $
, because of Condition (ii). Then, we introduce a new generator
![]() $c_{m+k+1}$
into (18), via the relation
$c_{m+k+1}$
into (18), via the relation
![]() $c_{m+k+1}=q^{-1}d_{m+k+1} r^{-1}$
. Then, we use this relation to eliminate the generator
$c_{m+k+1}=q^{-1}d_{m+k+1} r^{-1}$
. Then, we use this relation to eliminate the generator
![]() $d_{m+k+1}$
via
$d_{m+k+1}$
via
![]() $d_{m+k+1}=qc_{m+k+1}r=p_{m+k+1}$
. Thus, we obtain the presentation
$d_{m+k+1}=qc_{m+k+1}r=p_{m+k+1}$
. Thus, we obtain the presentation
which defines a group naturally isomorphic to the group defined by (18). The subgroup of this group generated by
![]() $p_1,\dots ,p_{m+k+1},d_{m+k+2},\dots ,d_n$
is isomorphic to the subgroup of (18) generated by
$p_1,\dots ,p_{m+k+1},d_{m+k+2},\dots ,d_n$
is isomorphic to the subgroup of (18) generated by
![]() $p_1,\dots ,p_{m+k},d_{m+k+1},\dots ,d_n$
, which, in turn, is isomorphic to
$p_1,\dots ,p_{m+k},d_{m+k+1},\dots ,d_n$
, which, in turn, is isomorphic to
![]() ${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
by induction. This completes the inductive proof. Putting
${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
by induction. This completes the inductive proof. Putting
![]() $k=n-m$
, we obtain that the subgroup of (17) generated by
$k=n-m$
, we obtain that the subgroup of (17) generated by
![]() $p_1,\dots ,p_n$
is naturally isomorphic to
$p_1,\dots ,p_n$
is naturally isomorphic to
![]() ${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
, and this completes the proof of the theorem.
${\operatorname {Gp}\bigl \langle {X}\:|\:{r=1} \bigr \rangle }$
, and this completes the proof of the theorem.
Corollary 3.13. Let
![]() $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, and let
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, and let
![]() $r \equiv r_1 \ldots r_k$
be the factorisation of r into minimal invertible pieces. If there is a basis
$r \equiv r_1 \ldots r_k$
be the factorisation of r into minimal invertible pieces. If there is a basis
![]() $p_1, \ldots , p_n$
of
$p_1, \ldots , p_n$
of
![]() ${\operatorname {Gp}\bigl \langle {r_1, \ldots , r_k} \bigr \rangle }\leq F_A$
satisfying the condition in the statement of Theorem 3.11, then the group of units of M is a one-relator group. Specifically, expressing each
${\operatorname {Gp}\bigl \langle {r_1, \ldots , r_k} \bigr \rangle }\leq F_A$
satisfying the condition in the statement of Theorem 3.11, then the group of units of M is a one-relator group. Specifically, expressing each
![]() $r_j=r_j^\prime (p_1,\dots , p_n)$
in
$r_j=r_j^\prime (p_1,\dots , p_n)$
in
![]() $F_A$
, where
$F_A$
, where
![]() $r_j^\prime \in \overline {\{x_1,\dots ,x_n\}}^\ast $
, the group of units of M is defined by
$r_j^\prime \in \overline {\{x_1,\dots ,x_n\}}^\ast $
, the group of units of M is defined by
As a special case of Theorem 3.11, we see that any sets
![]() $\{p_1,\dots ,p_n\}\subseteq F_A$
of the following types are free for substitutions into any one-relator presentations:
$\{p_1,\dots ,p_n\}\subseteq F_A$
of the following types are free for substitutions into any one-relator presentations:
-
(F1)
 $p_i$
s are powers of distinct generators from A (this is Corollary 4.10.2 in [Reference Magnus, Karrass and Solitar19]);
$p_i$
s are powers of distinct generators from A (this is Corollary 4.10.2 in [Reference Magnus, Karrass and Solitar19]); -
(F2)
 $p_i$
s are words over disjoint subalphabets of A;
$p_i$
s are words over disjoint subalphabets of A; -
(F3) for each
 $p_i$
, there exists a letter
$p_i$
, there exists a letter
 $a_i\in A$
which appears in
$a_i\in A$
which appears in
 $p_i$
precisely once, and does not appear in any
$p_i$
precisely once, and does not appear in any
 $p_j$
with
$p_j$
with
 $j<i$
.
$j<i$
.
We do not know whether the assumptions in Theorems 3.8 or 3.11 actually imply that the sets in question are free for substitutions in any presentations. However, this is the case for the above-listed special instances, as we shall see in the next theorem. At this point, it is very natural to wonder whether for a set of pieces to be free for substitutions, it might suffice just to assume that the set of words is Nielsen reduced (see [Reference Lyndon and Schupp18, page 6]). We will see later in Section 5.2 that the answer to this question is no (see Proposition 5.1).
Theorem 3.14. If
![]() $p_1,\dots , p_n\in F_A$
satisfy any of (F1), (F2) or (F3), then
$p_1,\dots , p_n\in F_A$
satisfy any of (F1), (F2) or (F3), then
![]() $\{p_1,\dots , p_n\}$
is free for substitution into any presentation.
$\{p_1,\dots , p_n\}$
is free for substitution into any presentation.
Proof. (F1) is a special case of (F2), so there is no need to prove it separately. Suppose that (F2) is satisfied. We need to prove that for any group
![]() $G={\operatorname {Gp}\bigl \langle {X}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
, with
$G={\operatorname {Gp}\bigl \langle {X}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
, with
![]() $X=\{x_1,\dots ,x_n\}$
, it naturally embeds into
$X=\{x_1,\dots ,x_n\}$
, it naturally embeds into
To this end, for
![]() $k=1,\dots ,n$
, let
$k=1,\dots ,n$
, let
![]() $A_k\subseteq A$
be the set of letters that appear in
$A_k\subseteq A$
be the set of letters that appear in
![]() $p_i$
, let
$p_i$
, let
![]() ${A^\prime =A\setminus (A_1\cup \dots \cup A_n)}$
and let
${A^\prime =A\setminus (A_1\cup \dots \cup A_n)}$
and let
We claim that for all
![]() $k=1,\dots ,n-1$
, the group
$k=1,\dots ,n-1$
, the group
![]() $G_k$
embeds naturally into
$G_k$
embeds naturally into
![]() $G_{k+1}$
via
$G_{k+1}$
via
 $$ \begin{align*} a &\mapsto a &\hspace{-50pt}& (a\in A_1\cup\dots\cup A_{k-1}\cup A^\prime),\\ x_k&\mapsto p_k, &\hspace{-63pt}&\\ x_j&\mapsto x_j &\hspace{-63pt}&(j=k+1,\dots,n). \end{align*} $$
$$ \begin{align*} a &\mapsto a &\hspace{-50pt}& (a\in A_1\cup\dots\cup A_{k-1}\cup A^\prime),\\ x_k&\mapsto p_k, &\hspace{-63pt}&\\ x_j&\mapsto x_j &\hspace{-63pt}&(j=k+1,\dots,n). \end{align*} $$
Once the claim is proved, composing all these embeddings together with the obvious embedding of
![]() ${\operatorname {Gp}\bigl \langle {X}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
into
${\operatorname {Gp}\bigl \langle {X}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
into
gives the desired embedding of
![]() ${\operatorname {Gp}\bigl \langle {X}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
into (19).
${\operatorname {Gp}\bigl \langle {X}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
into (19).
To prove the claim, let m be the order of
![]() $x_k$
in
$x_k$
in
![]() $G_k$
if this is finite, and otherwise let
$G_k$
if this is finite, and otherwise let
![]() $m=0$
. Note that by [Reference Magnus, Karrass and Solitar19, Corollary 4.4.11], the element
$m=0$
. Note that by [Reference Magnus, Karrass and Solitar19, Corollary 4.4.11], the element
![]() $p_k$
in the group
$p_k$
in the group
![]() ${\operatorname {Gp}\bigl \langle {A_k}\:|\:{p_k^m=1} \bigr \rangle }$
has finite order if and only if
${\operatorname {Gp}\bigl \langle {A_k}\:|\:{p_k^m=1} \bigr \rangle }$
has finite order if and only if
![]() $m>0$
, and that in this case, the order is precisely m. It follows that we can form the free product with amalgamation of the group
$m>0$
, and that in this case, the order is precisely m. It follows that we can form the free product with amalgamation of the group
![]() $G_k$
with the group
$G_k$
with the group
![]() ${\operatorname {Gp}\bigl \langle {A_k}\:|\:{p_k^m=1} \bigr \rangle }$
, amalgamating the subgroup
${\operatorname {Gp}\bigl \langle {A_k}\:|\:{p_k^m=1} \bigr \rangle }$
, amalgamating the subgroup
![]() ${\operatorname {Gp}\bigl \langle {x_k} \bigr \rangle }$
of the former with
${\operatorname {Gp}\bigl \langle {x_k} \bigr \rangle }$
of the former with
![]() ${\operatorname {Gp}\bigl \langle {p_k} \bigr \rangle }$
of the latter. This group naturally embeds
${\operatorname {Gp}\bigl \langle {p_k} \bigr \rangle }$
of the latter. This group naturally embeds
![]() $G_k$
and has the presentation
$G_k$
and has the presentation
Eliminate
![]() $x_k$
using the last relation in this presentation, to obtain
$x_k$
using the last relation in this presentation, to obtain
Notice that the specified mapping is certainly a homomorphism, and hence,
![]() $p_k^m$
is a consequence of the relations
$p_k^m$
is a consequence of the relations
![]() $r_i(p_1,\dots ,p_k,x_{k+1},\dots ,x_n)=1$
(
$r_i(p_1,\dots ,p_k,x_{k+1},\dots ,x_n)=1$
(
![]() $i\in I$
). Eliminating it yields the presentation for
$i\in I$
). Eliminating it yields the presentation for
![]() $G_{k+1}$
and proves the claim, and hence this case of the theorem.
$G_{k+1}$
and proves the claim, and hence this case of the theorem.
Suppose now that (F3) holds. Write
and let
![]() $A^\prime =A\setminus \{a_1,\dots ,a_n\}$
. Let
$A^\prime =A\setminus \{a_1,\dots ,a_n\}$
. Let
![]() $X=\{x_1,\dots ,x_n\}$
and consider arbitrary
$X=\{x_1,\dots ,x_n\}$
and consider arbitrary
![]() $r_i=r_i(x_1,\dots , x_n)\in \overline {X}^\ast $
(
$r_i=r_i(x_1,\dots , x_n)\in \overline {X}^\ast $
(
![]() $i\in I$
). We need to show that the group
$i\in I$
). We need to show that the group
naturally embeds into
It is clear that (20) embeds into
By assumption,
![]() $p_j^\prime ,p_j^{\prime \prime }\in \overline {A^\prime }^\ast $
, so in (22), we can introduce redundant generators
$p_j^\prime ,p_j^{\prime \prime }\in \overline {A^\prime }^\ast $
, so in (22), we can introduce redundant generators
![]() $a_1,\dots ,a_n$
as follows:
$a_1,\dots ,a_n$
as follows:
 $$ \begin{align*} &{\operatorname{Gp}\bigl\langle {A^\prime,a_1,\dots,a_n,X}\:|\:{r_i(x_1,\dots,x_n)=1\ (i\in I),\ a_j^{\epsilon_j}=(p_j^\prime)^{-1}x_j(p_j^{\prime\prime})^{-1}\ (j=1,\dots,n)} \bigr\rangle}\\ =\ & {\operatorname{Gp}\bigl\langle {A,X}\:|\:{r_i(x_1,\dots,x_n)\ (i\in I),\ x_j=p_j\ (j=1,\dots,n)} \bigr\rangle}. \end{align*} $$
$$ \begin{align*} &{\operatorname{Gp}\bigl\langle {A^\prime,a_1,\dots,a_n,X}\:|\:{r_i(x_1,\dots,x_n)=1\ (i\in I),\ a_j^{\epsilon_j}=(p_j^\prime)^{-1}x_j(p_j^{\prime\prime})^{-1}\ (j=1,\dots,n)} \bigr\rangle}\\ =\ & {\operatorname{Gp}\bigl\langle {A,X}\:|\:{r_i(x_1,\dots,x_n)\ (i\in I),\ x_j=p_j\ (j=1,\dots,n)} \bigr\rangle}. \end{align*} $$
Eliminating the
![]() $x_j$
from the last presentation yields the group (21), showing that it is isomorphic to (22), and thus naturally embedding (20), as required.
$x_j$
from the last presentation yields the group (21), showing that it is isomorphic to (22), and thus naturally embedding (20), as required.
Corollary 3.15. Let
![]() $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
be any special inverse monoid, and let
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
be any special inverse monoid, and let
![]() $r_i \equiv r_{i1} \ldots r_{ik_i}$
be the factorisation of
$r_i \equiv r_{i1} \ldots r_{ik_i}$
be the factorisation of
![]() $r_i$
into minimal invertible pieces. If there is a basis
$r_i$
into minimal invertible pieces. If there is a basis
![]() $p_1, \ldots , p_n$
of
$p_1, \ldots , p_n$
of
![]() ${\operatorname {Gp}\bigl \langle {\{ r_{ij}\::\: i\in I,\ 1\leq j\leq k_i\}} \bigr \rangle } \leq F_A$
satisfying any of (F1), (F2) or (F3), then the group of units U of M can be defined by a presentation with generators A and
${\operatorname {Gp}\bigl \langle {\{ r_{ij}\::\: i\in I,\ 1\leq j\leq k_i\}} \bigr \rangle } \leq F_A$
satisfying any of (F1), (F2) or (F3), then the group of units U of M can be defined by a presentation with generators A and
![]() $|I|$
many defining relations. Specifically, if each
$|I|$
many defining relations. Specifically, if each
![]() $r_{ij}$
is written as
$r_{ij}$
is written as
![]() $r_{ij}=r_{ij}^\prime (p_1,\dots ,p_n)$
, where
$r_{ij}=r_{ij}^\prime (p_1,\dots ,p_n)$
, where
![]() $r_{ij}^\prime \in \overline {\{x_1,\dots ,x_n\}}^\ast $
, then U is defined by
$r_{ij}^\prime \in \overline {\{x_1,\dots ,x_n\}}^\ast $
, then U is defined by
Proof. This analogous to Corollary 3.13.
4 An approach to computing pieces via regular languages
There already is in the literature an algorithm for computing a decomposition into invertible pieces. It was originally introduced by Adjan [Reference Adjan1], and modified by Zhang [Reference Zhang30]. It was designed for the setting of special monoid presentations, rather than inverse monoid presentations, but in fact remains valid for the latter as well.
The description we now give of the Adjan overlap algorithm follows that given by Lallement in [Reference Lallement14], who was chiefly concerned with one-relator monoids
![]() ${\operatorname {Mon}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
. Here, we shall explain the natural generalisation of that algorithm to arbitrary finitely presented special monoids
${\operatorname {Mon}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
. Here, we shall explain the natural generalisation of that algorithm to arbitrary finitely presented special monoids
![]() ${\operatorname {Mon}\bigl \langle {A}\:|\:{r_i \; (i \in I)} \bigr \rangle }$
. In general, this algorithm will compute a decomposition of the relators into pieces, but these will not in general be the minimal pieces (see Example 4.2 below). However, in the particular case of one-relator monoids
${\operatorname {Mon}\bigl \langle {A}\:|\:{r_i \; (i \in I)} \bigr \rangle }$
. In general, this algorithm will compute a decomposition of the relators into pieces, but these will not in general be the minimal pieces (see Example 4.2 below). However, in the particular case of one-relator monoids
![]() ${\operatorname {Mon}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, an important theorem of Adjan [Reference Adjan1] shows that this algorithm does compute the minimal invertible pieces of the defining relator r.
${\operatorname {Mon}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, an important theorem of Adjan [Reference Adjan1] shows that this algorithm does compute the minimal invertible pieces of the defining relator r.
Let
![]() $M= {\operatorname {Mon}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
be a special monoid, and set
$M= {\operatorname {Mon}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
be a special monoid, and set
![]() $R = \{r_i \::\: i \in I\}$
. We say that a submonoid T of the free monoid
$R = \{r_i \::\: i \in I\}$
. We say that a submonoid T of the free monoid
![]() $A^{*}$
has property
$A^{*}$
has property
![]() $({\mathcal {A}})$
if
$({\mathcal {A}})$
if
-
(
 ${\mathcal {A}}$
) For all
${\mathcal {A}}$
) For all
 $\alpha , \beta , \gamma \in A^{*}$
, if
$\alpha , \beta , \gamma \in A^{*}$
, if
 $\alpha \beta \in T$
and
$\alpha \beta \in T$
and
 $\beta \gamma \in T$
then
$\beta \gamma \in T$
then
 $\{\alpha ,\beta ,\gamma \} \subseteq T$
.
$\{\alpha ,\beta ,\gamma \} \subseteq T$
.
Let
![]() $U(R)$
be the smallest submonoid of
$U(R)$
be the smallest submonoid of
![]() $A^{*}$
, such that
$A^{*}$
, such that
![]() $R \subseteq U(R)$
and
$R \subseteq U(R)$
and
![]() $U(R)$
satisfies (
$U(R)$
satisfies (
![]() $\mathcal {A}$
).
$\mathcal {A}$
).
To see that the monoid
![]() $U(R)$
exists, note that the set of submonoids of
$U(R)$
exists, note that the set of submonoids of
![]() $A^{*}$
containing R and satisfying (
$A^{*}$
containing R and satisfying (
![]() ${\mathcal {A}}$
) is nonempty (since e.g.
${\mathcal {A}}$
) is nonempty (since e.g.
![]() $A^{*}$
satisfies these properties), and it follows from the definitions that the intersection of any family of submonoids of
$A^{*}$
satisfies these properties), and it follows from the definitions that the intersection of any family of submonoids of
![]() $A^{*}$
with these properties again gives a submonoid of
$A^{*}$
with these properties again gives a submonoid of
![]() $A^{*}$
with these properties.
$A^{*}$
with these properties.
Recall that a subset C of
![]() $A^+$
is called a code if C is a set of free generators for the submonoid
$A^+$
is called a code if C is a set of free generators for the submonoid
![]() ${\operatorname {Mon}\bigl \langle {C} \bigr \rangle } \leq A^+$
. A subset C of
${\operatorname {Mon}\bigl \langle {C} \bigr \rangle } \leq A^+$
. A subset C of
![]() $A^+$
is said to have the prefix property if
$A^+$
is said to have the prefix property if
![]() $CA^+ \cap C = \varnothing $
. Similarly, we say C has the suffix property if
$CA^+ \cap C = \varnothing $
. Similarly, we say C has the suffix property if
![]() $C \cap A^+C = \varnothing $
. Any subset C of
$C \cap A^+C = \varnothing $
. Any subset C of
![]() $A^+$
with the prefix property is a code. We call these prefix codes. Similarly, if C has the suffix property, then C is a code called a suffix code. If C is both a prefix and a suffix code, then we call C a biprefix code.
$A^+$
with the prefix property is a code. We call these prefix codes. Similarly, if C has the suffix property, then C is a code called a suffix code. If C is both a prefix and a suffix code, then we call C a biprefix code.
We now make some observations about the set
![]() $U(R)$
.
$U(R)$
.
-
(a) Every word
 $w \in U(R)$
represents and invertible element of the monoid M.
$w \in U(R)$
represents and invertible element of the monoid M. -
(b)
 $U(R)$
is a free monoid which is freely generated by a finite biprefix code
$U(R)$
is a free monoid which is freely generated by a finite biprefix code
 $B(R)$
.
$B(R)$
. -
(c) There is an algorithm which takes any finite set R of words as input and computes the biprefix code
 $B(R)$
.
$B(R)$
.
For proofs of these facts, we refer the reader to [Reference Lallement14, Section 1]. The idea behind the proof of (a) is to observe that if
![]() $\gamma $
and
$\gamma $
and
![]() $\delta $
are words that represent invertible elements of M, then so does their product, and also, if
$\delta $
are words that represent invertible elements of M, then so does their product, and also, if
![]() $\alpha \beta $
and
$\alpha \beta $
and
![]() $\beta \gamma $
are words that represent invertible elements of M, then the words
$\beta \gamma $
are words that represent invertible elements of M, then the words
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
all also represent invertible elements of M. The starting point for the algorithm is provided by the members of R, which, being equal to
$\gamma $
all also represent invertible elements of M. The starting point for the algorithm is provided by the members of R, which, being equal to
![]() $1$
in M, certainly represent invertible elements. Since
$1$
in M, certainly represent invertible elements. Since
![]() $U(R)$
is obtained from R by closing under taking products and under adding triples of words
$U(R)$
is obtained from R by closing under taking products and under adding triples of words
![]() $\alpha , \beta $
and
$\alpha , \beta $
and
![]() $\gamma $
to ensure condition (
$\gamma $
to ensure condition (
![]() ${\mathcal {A}}$
), this can be used to prove (a).
${\mathcal {A}}$
), this can be used to prove (a).
Regarding (a), it is important to note that even for one-relator monoids, we are not claiming that every word which represents an invertible element of M necessarily belongs to the set
![]() $U(R)$
. Indeed, if one considers the simple example of the bicyclic monoid
$U(R)$
. Indeed, if one considers the simple example of the bicyclic monoid
![]() ${\operatorname {Mon}\bigl \langle {b,c}\:|\:{bc=1} \bigr \rangle }$
, then clearly
${\operatorname {Mon}\bigl \langle {b,c}\:|\:{bc=1} \bigr \rangle }$
, then clearly
![]() $U(R) = \{bc\}^{*}$
is the smallest submonoid of
$U(R) = \{bc\}^{*}$
is the smallest submonoid of
![]() $\{b,c\}^{*}$
which contains
$\{b,c\}^{*}$
which contains
![]() $\{bc\}$
and has property (
$\{bc\}$
and has property (
![]() ${\mathcal {A}}$
). But the word
${\mathcal {A}}$
). But the word
![]() $bbcc$
is equal to
$bbcc$
is equal to
![]() $1$
in the bicyclic monoid, so certainly represents an invertible element, while
$1$
in the bicyclic monoid, so certainly represents an invertible element, while
![]() $bbcc \not \in \{bc\}^{*} = U(R)$
.
$bbcc \not \in \{bc\}^{*} = U(R)$
.
Even though we do not need it in this paper, for the sake of completeness, we explain here an algorithm which computes the finite biprefix code
![]() $B(R)$
that generates the free monoid
$B(R)$
that generates the free monoid
![]() $U(R)$
. This description follows [Reference Lallement14, page 372] (with a small correction we have made to a typo in (i) on [Reference Lallement14, page 372]).
$U(R)$
. This description follows [Reference Lallement14, page 372] (with a small correction we have made to a typo in (i) on [Reference Lallement14, page 372]).
For
![]() $i \in \mathbb {N}$
, we define the set
$i \in \mathbb {N}$
, we define the set
![]() $W_i$
inductively as follows. First, set
$W_i$
inductively as follows. First, set
![]() $W_0 = R = \{r_i \::\: i \in I \}$
. Then, for
$W_0 = R = \{r_i \::\: i \in I \}$
. Then, for
![]() $i>0$
, we define
$i>0$
, we define
![]() $W_i$
inductively in the following way. For
$W_i$
inductively in the following way. For
![]() $u \in A^{*}$
, we have
$u \in A^{*}$
, we have
![]() $u \in W_{i+1}$
if and only if one of the following conditions holds:
$u \in W_{i+1}$
if and only if one of the following conditions holds:
-
(i)
 $u \in W_i$
and
$u \in W_i$
and
 $v \not \in \operatorname {\mathrm {pref}}(u)$
and
$v \not \in \operatorname {\mathrm {pref}}(u)$
and
 $v \not \in \operatorname {\mathrm {suff}}(u)$
for all
$v \not \in \operatorname {\mathrm {suff}}(u)$
for all
 $v \in W_i \setminus \{ u \}$
;
$v \in W_i \setminus \{ u \}$
; -
(ii) there exist
 $v, v' \in X^{*}$
not both equal to
$v, v' \in X^{*}$
not both equal to
 $\epsilon $
, such that
$\epsilon $
, such that
 $uv \in W_i$
and
$uv \in W_i$
and
 $v'u \in W_i$
;
$v'u \in W_i$
; -
(iii) there exist
 $v, v' \in X^{*}$
with
$v, v' \in X^{*}$
with
 $v \neq \epsilon $
, such that
$v \neq \epsilon $
, such that
 $uv \in W_i$
and
$uv \in W_i$
and
 $vv' \in W_i$
;
$vv' \in W_i$
; -
(iv) there exist
 $v,v' \in X$
with
$v,v' \in X$
with
 $v' \neq \epsilon $
, such that
$v' \neq \epsilon $
, such that
 $v'u \in W_i$
and
$v'u \in W_i$
and
 $vv' \in W_i$
.
$vv' \in W_i$
.
It may be shown that there is a number n, such that
![]() $W_n = W_{n'}$
for all
$W_n = W_{n'}$
for all
![]() $n' \geq n$
that is this process eventually stabilises. Then
$n' \geq n$
that is this process eventually stabilises. Then
![]() $B(R) = W_n$
is a biprefix code that freely generates
$B(R) = W_n$
is a biprefix code that freely generates
![]() $B(R)$
(see [Reference Lallement14, Theorem 1(i)]). Roughly speaking, the idea behind the above algorithm is that steps (ii)–(iv) are designed to ensure that the set we construct does satisfy property (
$B(R)$
(see [Reference Lallement14, Theorem 1(i)]). Roughly speaking, the idea behind the above algorithm is that steps (ii)–(iv) are designed to ensure that the set we construct does satisfy property (
![]() ${\mathcal {A}}$
), while step (i) ensures that the set constructed has the prefix and suffix properties.
${\mathcal {A}}$
), while step (i) ensures that the set constructed has the prefix and suffix properties.
Since
![]() $B(R)$
is a code which generates the free monoid
$B(R)$
is a code which generates the free monoid
![]() $U(R)$
, it follows that every word
$U(R)$
, it follows that every word
![]() $w \in U(R)$
can be written uniquely as
$w \in U(R)$
can be written uniquely as
![]() $w \equiv w_1 \ldots w_k$
, where
$w \equiv w_1 \ldots w_k$
, where
![]() $w_i \in B(R)$
for
$w_i \in B(R)$
for
![]() $1 \leq i \leq k$
. Since
$1 \leq i \leq k$
. Since
![]() $R \subseteq U(R)$
, it follows that, in particular, every relator word
$R \subseteq U(R)$
, it follows that, in particular, every relator word
![]() $r_i$
with
$r_i$
with
![]() $i \in I$
decomposes uniquely as a product of words from
$i \in I$
decomposes uniquely as a product of words from
![]() $B(R)$
. We call this the decomposition of relators into invertible pieces determined by the Adjan algorithm. The key result showing the importance of this algorithm is that for special one-relator monoids, this algorithm actually computes the decomposition of the relator into minimal invertible pieces. We have already seen that the presentation determined by these pieces is then a presentation for the group of units of the monoid (see Theorem 1.2). This gives the following result of Adjan [Reference Adjan1].
$B(R)$
. We call this the decomposition of relators into invertible pieces determined by the Adjan algorithm. The key result showing the importance of this algorithm is that for special one-relator monoids, this algorithm actually computes the decomposition of the relator into minimal invertible pieces. We have already seen that the presentation determined by these pieces is then a presentation for the group of units of the monoid (see Theorem 1.2). This gives the following result of Adjan [Reference Adjan1].
Theorem 4.1 (Adjan [Reference Adjan1, Chapter III, Theorem 7])
For any one-relator special monoid
![]() ${\operatorname {Mon}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, the Adjan algorithm computes the decomposition of r into minimal invertible pieces. More precisely, the biprefix code
${\operatorname {Mon}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, the Adjan algorithm computes the decomposition of r into minimal invertible pieces. More precisely, the biprefix code
![]() $B(\{r\})$
computed by the Adjan algorithm is equal to the set of minimal invertible pieces of the relator r. Hence, there is an algorithm that takes any special one-relator monoid as input, and computes a one-relator presentation which is isomorphic to the group of units of the monoid.
$B(\{r\})$
computed by the Adjan algorithm is equal to the set of minimal invertible pieces of the relator r. Hence, there is an algorithm that takes any special one-relator monoid as input, and computes a one-relator presentation which is isomorphic to the group of units of the monoid.
For arbitrary special monoid presentations, this result is no longer true, as the following example demonstrates.
Example 4.2. Consider the monoid presentation
There are no overlaps, but
![]() $d = 1$
is easily seen to be a consequence of the defining relations. In particular, the letter d represents an invertible element. From this it follows that all the letters here are invertible, but this is not something that the Adjan algorithm will discover.
$d = 1$
is easily seen to be a consequence of the defining relations. In particular, the letter d represents an invertible element. From this it follows that all the letters here are invertible, but this is not something that the Adjan algorithm will discover.
In fact, it is proved in [Reference Narendran, Ó’Dúnlang and Otto23] that the problem of whether a finitely presented special monoid is a group is undecidable. From this, it follows that there is no algorithm which takes finite special monoid presentations as input and computes the minimal invertible pieces of the relator.
It is natural to ask whether there is an algorithm which takes finite one-relator special inverse monoid
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
as input and computes the minimal invertible pieces of the relator r. This is a question that was considered by Margolis et al. in [Reference Margolis, Meakin and Stephen22]. As already mentioned above, in that paper, the following example is introduced
${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
as input and computes the minimal invertible pieces of the relator r. This is a question that was considered by Margolis et al. in [Reference Margolis, Meakin and Stephen22]. As already mentioned above, in that paper, the following example is introduced
called the O’Hare monoid. As explained above, one thing that makes this example significant is that the defining relator word clearly has no overlaps with itself, and hence, the Adjan overlap algorithm would terminate instantly, and return r as a single invertible piece of itself. However, Margolis et al. [Reference Margolis, Meakin and Stephen22], using van Kampen diagrams and Stephen’s procedure, succeed in showing that r in fact has a finer decomposition, namely
They provide no further information about the group of units of the monoid
![]() ${\mathcal {O}}$
.
${\mathcal {O}}$
.
Our aim now is to give a unit computing algorithm for special inverse monoid presentations, which improves on the Adjan algorithm. Specifically, our new algorithm, which we shall call the Benois algorithm, will have the following properties
-
(1) it correctly computes the minimal invertible pieces of the O’Hare example, and
-
(2) it always computes a refinement of the Adjan algorithm.
These properties mean that every invertible piece that the Adjan algorithm discovers, the Benois algorithm also discovers, and there are examples where the Benois algorithm discovers strictly smaller pieces than the Adjan algorithm does.
Let
![]() $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
be a finitely presented special inverse monoid. Let
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1\ (i\in I)} \bigr \rangle }$
be a finitely presented special inverse monoid. Let
Let
![]() $V = \mathrm {red}(\Sigma ^{*}) \subseteq F_A$
. For each
$V = \mathrm {red}(\Sigma ^{*}) \subseteq F_A$
. For each
![]() $i \in I$
, decompose
$i \in I$
, decompose
such that for every proper prefix p of
![]() $r_i$
, we have
$r_i$
, we have
Intuitively, this decomposition is obtained by ‘reading’
![]() $r_i$
from left to right, and ‘marking’ each prefix p with the property that
$r_i$
from left to right, and ‘marking’ each prefix p with the property that
![]() $\mathrm {red}(p^{-1})\in V$
.
$\mathrm {red}(p^{-1})\in V$
.
Lemma 4.3. For each
![]() $i \in I$
, the factorisation (23) is a decomposition into invertible pieces.
$i \in I$
, the factorisation (23) is a decomposition into invertible pieces.
Proof. We need to prove that each
![]() $r_{ij}$
represents an invertible element of M. This is equivalent to each prefix
$r_{ij}$
represents an invertible element of M. This is equivalent to each prefix
![]() $p_{ij}\equiv r_{i1}r_{i2}\dots r_{ij}$
being invertible, and we proceed to prove this latter assertion. Since every word in
$p_{ij}\equiv r_{i1}r_{i2}\dots r_{ij}$
being invertible, and we proceed to prove this latter assertion. Since every word in
![]() $\Sigma $
clearly represents a right invertible element of M, it follows that every word in
$\Sigma $
clearly represents a right invertible element of M, it follows that every word in
![]() $\Sigma ^{*}$
represents a right invertible element of M. Applying Lemma 2.2(iii) it follows that every word in V represents a right invertible element of M. Since
$\Sigma ^{*}$
represents a right invertible element of M. Applying Lemma 2.2(iii) it follows that every word in V represents a right invertible element of M. Since
![]() $p_{ij}$
represents a right invertible element of M it follows from Lemma 2.2(iii) that
$p_{ij}$
represents a right invertible element of M it follows from Lemma 2.2(iii) that
![]() $p _{ij}= \operatorname {\mathrm {red}}(p_{ij})$
in M. The word
$p _{ij}= \operatorname {\mathrm {red}}(p_{ij})$
in M. The word
![]() $p_{ij}^{-1}$
represents a left invertible element of M, and hence,
$p_{ij}^{-1}$
represents a left invertible element of M, and hence,
![]() $p_{ij}^{-1} = \operatorname {\mathrm {red}}(p_{ij}^{-1})$
also holds in M by an obvious dual of Lemma 2.2(iii). By (24), we have
$p_{ij}^{-1} = \operatorname {\mathrm {red}}(p_{ij}^{-1})$
also holds in M by an obvious dual of Lemma 2.2(iii). By (24), we have
![]() $\operatorname {\mathrm {red}}(p_{ij}^{-1}) \in V$
, implying that
$\operatorname {\mathrm {red}}(p_{ij}^{-1}) \in V$
, implying that
![]() $p_{ij}^{-1}$
represents a right invertible element of M, and therefore
$p_{ij}^{-1}$
represents a right invertible element of M, and therefore
![]() $p_{ij}$
represents an invertible element of M, as required.
$p_{ij}$
represents an invertible element of M, as required.
Note that this lemma does not claim that (23) is a decomposition into minimal invertible pieces. In fact, it remains an open question whether this is the case.
Next, we turn our attention to the question of whether the above decomposition of the relations into invertible pieces is computable. It is a consequence of a theorem of Benois that the free group
![]() $F_A$
has a decidable submonoid membership problem (see [Reference Lohrey15] and the references to Benois’s original work therein).
$F_A$
has a decidable submonoid membership problem (see [Reference Lohrey15] and the references to Benois’s original work therein).
Lemma 4.4. There is an algorithm which takes any finite inverse monoid presentation
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r_i = 1 \; (i \in I)} \bigr \rangle }$
and any word
${\operatorname {Inv}\bigl \langle {A}\:|\:{r_i = 1 \; (i \in I)} \bigr \rangle }$
and any word
![]() $w \in \overline {A}^{*}$
, and decides whether
$w \in \overline {A}^{*}$
, and decides whether
![]() $\mathrm {red}(w) \in V$
. Therefore, there is an algorithm which takes any finite inverse monoid presentation
$\mathrm {red}(w) \in V$
. Therefore, there is an algorithm which takes any finite inverse monoid presentation
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r_i = 1 \; (i \in I)} \bigr \rangle }$
and computes the decomposition into invertible pieces given by (23) for all relators
${\operatorname {Inv}\bigl \langle {A}\:|\:{r_i = 1 \; (i \in I)} \bigr \rangle }$
and computes the decomposition into invertible pieces given by (23) for all relators
![]() $r_i$
in the presentation.
$r_i$
in the presentation.
Proof. By definition, the set V is a finitely generated submonoid of the free group
![]() $F_A$
, and the word
$F_A$
, and the word
![]() $\operatorname {\mathrm {red}}(w)$
is an element of the free group
$\operatorname {\mathrm {red}}(w)$
is an element of the free group
![]() $F_A$
. Hence, Benois’ theorem can be applied to decide whether or not
$F_A$
. Hence, Benois’ theorem can be applied to decide whether or not
![]() $\operatorname {\mathrm {red}}(w) \in V$
. The second assertion in the statement of the lemma is then immediate.
$\operatorname {\mathrm {red}}(w) \in V$
. The second assertion in the statement of the lemma is then immediate.
We shall call the algorithm for computing invertible pieces given in Lemma 4.4 the Benois algorithm.
Our aim is to prove the following result, which explains the relationship between the Benois algorithm and the Adjan algorithm.
Theorem 4.5. Let
![]() $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1 (i \in I)} \bigr \rangle }$
. Then, for all
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i=1 (i \in I)} \bigr \rangle }$
. Then, for all
![]() $i \in I$
, the decomposition of
$i \in I$
, the decomposition of
![]() $r_i$
into pieces computed by the Benois algorithm is a refinement of the decomposition computed by the Adjan algorithm.
$r_i$
into pieces computed by the Benois algorithm is a refinement of the decomposition computed by the Adjan algorithm.
We need a few more definitions and lemmas before we can prove Theorem 4.5. For any two words
![]() $\alpha , \beta \in \overline {A}^{*}$
, we write
$\alpha , \beta \in \overline {A}^{*}$
, we write
![]() $\alpha \rightarrow \beta $
if
$\alpha \rightarrow \beta $
if
![]() $\beta $
can be obtained from
$\beta $
can be obtained from
![]() $\alpha $
by a single application of a rewrite rule
$\alpha $
by a single application of a rewrite rule
![]() $xx^{-1} \rightarrow 1$
or
$xx^{-1} \rightarrow 1$
or
![]() $x^{-1}x \rightarrow 1$
(with
$x^{-1}x \rightarrow 1$
(with
![]() $x \in A$
). Let us write
$x \in A$
). Let us write
![]() $\rightarrow ^{*}$
for the reflexive transitive closure of
$\rightarrow ^{*}$
for the reflexive transitive closure of
![]() $\rightarrow $
that is
$\rightarrow $
that is
![]() $\alpha \rightarrow ^{*} \beta $
means that
$\alpha \rightarrow ^{*} \beta $
means that
![]() $\beta $
can be obtained from
$\beta $
can be obtained from
![]() $\alpha $
by a finite (possibly empty) sequence of deletions
$\alpha $
by a finite (possibly empty) sequence of deletions
![]() $xx^{-1} \rightarrow 1$
or
$xx^{-1} \rightarrow 1$
or
![]() $x^{-1}x \rightarrow 1$
. If
$x^{-1}x \rightarrow 1$
. If
![]() $\alpha \rightarrow ^{*} \beta $
, we say that
$\alpha \rightarrow ^{*} \beta $
, we say that
![]() $\alpha $
can be partially freely reduced to
$\alpha $
can be partially freely reduced to
![]() $\beta $
(partially, since
$\beta $
(partially, since
![]() $\beta $
need not be a reduced word).
$\beta $
need not be a reduced word).
Define
So
![]() ${\overrightarrow {\Sigma ^{*}}}$
is the closure of the set
${\overrightarrow {\Sigma ^{*}}}$
is the closure of the set
![]() $\Sigma ^{*}$
under partial free reduction
$\Sigma ^{*}$
under partial free reduction
![]() $\rightarrow ^{*}$
.
$\rightarrow ^{*}$
.
It follows from Lemma 2.2 that every word in
![]() ${\overrightarrow {\Sigma ^{*}}}$
represents a right invertible element of M.
${\overrightarrow {\Sigma ^{*}}}$
represents a right invertible element of M.
Remark 4.6. Although we do not need it here, it may be shown that
![]() ${\overrightarrow {\Sigma ^{*}}}$
is a regular language, that is there is a finite state automaton
${\overrightarrow {\Sigma ^{*}}}$
is a regular language, that is there is a finite state automaton
![]() $\mathcal {A}$
, such that the language
$\mathcal {A}$
, such that the language
![]() $L(\mathcal {A})$
recognised by the automaton is
$L(\mathcal {A})$
recognised by the automaton is
![]() $L(\mathcal {A}) = {\overrightarrow {\Sigma ^{*}}}$
. The proof of this can be found in [Reference Lohrey15]. The idea is to use an automaton saturation procedure. We begin with a finite state automaton
$L(\mathcal {A}) = {\overrightarrow {\Sigma ^{*}}}$
. The proof of this can be found in [Reference Lohrey15]. The idea is to use an automaton saturation procedure. We begin with a finite state automaton
![]() $\mathcal {B}$
with
$\mathcal {B}$
with
![]() $L(\mathcal {B})=\Sigma ^{*}$
and then add
$L(\mathcal {B})=\Sigma ^{*}$
and then add
![]() $\epsilon $
transitions wherever we can read
$\epsilon $
transitions wherever we can read
![]() $xx^{-1}$
, and repeat this process until no more
$xx^{-1}$
, and repeat this process until no more
![]() $\epsilon $
transitions need to be added. Note that given reduced word u, we can check if
$\epsilon $
transitions need to be added. Note that given reduced word u, we can check if
![]() $u \in V$
by testing whether
$u \in V$
by testing whether
![]() $u \in L(\mathcal {A})$
.
$u \in L(\mathcal {A})$
.
Define
![]() ${\mathcal {U}} \subseteq {\overrightarrow {\Sigma ^{*}}}$
in the following way
${\mathcal {U}} \subseteq {\overrightarrow {\Sigma ^{*}}}$
in the following way
Note that every word
![]() $u \in {\mathcal {U}}$
represents an invertible element of M.
$u \in {\mathcal {U}}$
represents an invertible element of M.
The important thing to note about the set
![]() ${\mathcal {U}}$
is the following: Let p be a prefix of some relator
${\mathcal {U}}$
is the following: Let p be a prefix of some relator
![]() $r_i$
with
$r_i$
with
![]() $i \in I$
. Then, by definition,
$i \in I$
. Then, by definition,
![]() $p \in \Sigma \subseteq {\overrightarrow {\Sigma ^{*}}}$
. If, in addition,
$p \in \Sigma \subseteq {\overrightarrow {\Sigma ^{*}}}$
. If, in addition,
![]() $p \in {\mathcal {U}}$
, then p is an invertible prefix of a relator, and we will prove below that this invertible prefix p will be computed by the Benois algorithm. However, it is very important to note that the converse need not be true since it is possible that
$p \in {\mathcal {U}}$
, then p is an invertible prefix of a relator, and we will prove below that this invertible prefix p will be computed by the Benois algorithm. However, it is very important to note that the converse need not be true since it is possible that
![]() $p \in {\overrightarrow {\Sigma ^{*}}}$
,
$p \in {\overrightarrow {\Sigma ^{*}}}$
,
![]() $p^{-1} \not \in {\overrightarrow {\Sigma ^{*}}}$
but
$p^{-1} \not \in {\overrightarrow {\Sigma ^{*}}}$
but
![]() $\operatorname {\mathrm {red}}(p^{-1}) \in {\overrightarrow {\Sigma ^{*}}}$
.
$\operatorname {\mathrm {red}}(p^{-1}) \in {\overrightarrow {\Sigma ^{*}}}$
.
Lemma 4.7. Let p be a prefix of the relator
![]() $r_i$
, where
$r_i$
, where
![]() $i \in I$
. If
$i \in I$
. If
![]() $p \in {\mathcal {U}}$
, then p is an invertible prefix of
$p \in {\mathcal {U}}$
, then p is an invertible prefix of
![]() $r_i$
computed by the Benois algorithm.
$r_i$
computed by the Benois algorithm.
Proof. Since
![]() $p \in {\mathcal {U}}$
, it follows by definition of
$p \in {\mathcal {U}}$
, it follows by definition of
![]() ${\mathcal {U}}$
that
${\mathcal {U}}$
that
![]() $p^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
. Hence
$p^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
. Hence
![]() $\operatorname {\mathrm {red}}(p^{-1}) \in {\overrightarrow {\Sigma ^{*}}}$
, since by definition the set
$\operatorname {\mathrm {red}}(p^{-1}) \in {\overrightarrow {\Sigma ^{*}}}$
, since by definition the set
![]() ${\overrightarrow {\Sigma ^{*}}}$
is closed under the operation of partial free reduction of words, and hence
${\overrightarrow {\Sigma ^{*}}}$
is closed under the operation of partial free reduction of words, and hence
It follows from the definition of the Benois algorithm that p is an invertible piece of
![]() $r_i$
computed by the Benois algorithm.
$r_i$
computed by the Benois algorithm.
Remark 4.8. It is important to note that we are not claiming that
![]() ${\mathcal {U}}$
contains all the invertible prefixes of relators computed by the Benois algorithm.
${\mathcal {U}}$
contains all the invertible prefixes of relators computed by the Benois algorithm.
We will now prove that
![]() ${\mathcal {U}}$
does contain all prefixes of relators computed by the Adjan algorithm. Combining this with Lemma 4.7 will prove Theorem 4.5.
${\mathcal {U}}$
does contain all prefixes of relators computed by the Adjan algorithm. Combining this with Lemma 4.7 will prove Theorem 4.5.
Lemma 4.9. Let
![]() $\gamma , \delta \in \overline {A}^{*}$
with
$\gamma , \delta \in \overline {A}^{*}$
with
![]() $\gamma \rightarrow \delta $
. Then for any decomposition
$\gamma \rightarrow \delta $
. Then for any decomposition
![]() $\delta \equiv \delta _1 \delta _2$
, there exists a decomposition
$\delta \equiv \delta _1 \delta _2$
, there exists a decomposition
![]() $\gamma \equiv \gamma _1 \gamma _2$
, such that
$\gamma \equiv \gamma _1 \gamma _2$
, such that
![]() $\gamma _1 \rightarrow ^{*} \delta _1$
and
$\gamma _1 \rightarrow ^{*} \delta _1$
and
![]() $\gamma _2 \rightarrow ^{*} \delta _2$
.
$\gamma _2 \rightarrow ^{*} \delta _2$
.
Proof. Since
![]() $\gamma \rightarrow \delta $
, we can write
$\gamma \rightarrow \delta $
, we can write
![]() $\gamma \equiv \gamma ' xx^{-1} \gamma "$
, where
$\gamma \equiv \gamma ' xx^{-1} \gamma "$
, where
![]() $\delta \equiv \gamma ' \gamma "$
and
$\delta \equiv \gamma ' \gamma "$
and
![]() $x \in \overline {A}$
.
$x \in \overline {A}$
.
Now we have
![]() $\delta _1 \delta _2 \equiv \delta \equiv \gamma ' \gamma "$
. Then
$\delta _1 \delta _2 \equiv \delta \equiv \gamma ' \gamma "$
. Then
![]() $\gamma '$
is a prefix of
$\gamma '$
is a prefix of
![]() $\delta _1$
, or else
$\delta _1$
, or else
![]() $\gamma ^{\prime \prime }$
is a suffix of
$\gamma ^{\prime \prime }$
is a suffix of
![]() $\delta _2$
. We consider the former case, and the latter is dealt with analogously. Write
$\delta _2$
. We consider the former case, and the latter is dealt with analogously. Write
![]() $\delta _1 \equiv \gamma ' \mu $
. So
$\delta _1 \equiv \gamma ' \mu $
. So
![]() $\gamma '\gamma " \equiv \delta \equiv \delta _1 \delta _2 \equiv \gamma ' \mu \delta _2$
. Hence,
$\gamma '\gamma " \equiv \delta \equiv \delta _1 \delta _2 \equiv \gamma ' \mu \delta _2$
. Hence,
![]() $\gamma " \equiv \mu \delta _2$
and so
$\gamma " \equiv \mu \delta _2$
and so
![]() $\gamma \equiv \gamma ' xx^{-1} \mu \delta _2$
. So if we set
$\gamma \equiv \gamma ' xx^{-1} \mu \delta _2$
. So if we set
![]() $\gamma _1 \equiv \gamma ' xx^{-1} \mu $
and
$\gamma _1 \equiv \gamma ' xx^{-1} \mu $
and
![]() $\gamma _2 \equiv \delta _2$
, then
$\gamma _2 \equiv \delta _2$
, then
![]() $\gamma \equiv \gamma _1 \gamma _2$
and
$\gamma \equiv \gamma _1 \gamma _2$
and
![]() $\gamma _1 \rightarrow ^{*} \gamma '\mu \equiv \delta _1$
and
$\gamma _1 \rightarrow ^{*} \gamma '\mu \equiv \delta _1$
and
![]() $\gamma _2 \rightarrow ^{*} \delta _2$
, as required.
$\gamma _2 \rightarrow ^{*} \delta _2$
, as required.
Corollary 4.10. Let
![]() $\gamma , \delta \in \overline {A}^{*}$
with
$\gamma , \delta \in \overline {A}^{*}$
with
![]() $\gamma \rightarrow ^{*} \delta $
. Then for any decomposition
$\gamma \rightarrow ^{*} \delta $
. Then for any decomposition
![]() $\delta \equiv \delta _1 \delta _2$
, there exists a decomposition
$\delta \equiv \delta _1 \delta _2$
, there exists a decomposition
![]() $\gamma \equiv \gamma _1 \gamma _2$
, such that
$\gamma \equiv \gamma _1 \gamma _2$
, such that
![]() $\gamma _1 \rightarrow ^{*} \delta _1$
and
$\gamma _1 \rightarrow ^{*} \delta _1$
and
![]() $\gamma _2 \rightarrow ^{*} \delta _2$
.
$\gamma _2 \rightarrow ^{*} \delta _2$
.
Proof. Since
![]() $\gamma \rightarrow ^{*} \delta $
, we can write
$\gamma \rightarrow ^{*} \delta $
, we can write
We have
![]() $w_k \equiv \delta \equiv \delta _1 \delta _2$
. Then applying Lemma 4.9 to
$w_k \equiv \delta \equiv \delta _1 \delta _2$
. Then applying Lemma 4.9 to
![]() $w_i \rightarrow w_{i+1}$
for all i, it follows that each
$w_i \rightarrow w_{i+1}$
for all i, it follows that each
![]() $w_i$
can be decomposed as
$w_i$
can be decomposed as
![]() $w_i \equiv w_i^{\prime } w_i^{\prime \prime }$
and
$w_i \equiv w_i^{\prime } w_i^{\prime \prime }$
and
Setting
![]() $\gamma _1 \equiv w_0^{\prime }$
and
$\gamma _1 \equiv w_0^{\prime }$
and
![]() $\gamma _2 \equiv w_0^{\prime \prime }$
then proves the result.
$\gamma _2 \equiv w_0^{\prime \prime }$
then proves the result.
Note that the set
![]() $\Sigma ^{*}$
is clearly prefix closed.
$\Sigma ^{*}$
is clearly prefix closed.
Lemma 4.11. The set
![]() ${\overrightarrow {\Sigma ^{*}}}$
is prefix closed, that is for any words
${\overrightarrow {\Sigma ^{*}}}$
is prefix closed, that is for any words
![]() $\alpha , \beta \in \overline {A}^{*}$
if
$\alpha , \beta \in \overline {A}^{*}$
if
![]() $\alpha \in {\overrightarrow {\Sigma ^{*}}}$
and
$\alpha \in {\overrightarrow {\Sigma ^{*}}}$
and
![]() $\beta $
is a prefix of
$\beta $
is a prefix of
![]() $\alpha $
, then
$\alpha $
, then
![]() $\beta \in {\overrightarrow {\Sigma ^{*}}}$
.
$\beta \in {\overrightarrow {\Sigma ^{*}}}$
.
Proof. Let
![]() $\beta $
be a prefix of
$\beta $
be a prefix of
![]() $\alpha $
. Write
$\alpha $
. Write
![]() $\alpha \equiv \beta \beta '$
. Since
$\alpha \equiv \beta \beta '$
. Since
![]() $\alpha \in {\overrightarrow {\Sigma ^{*}}}$
, there exists a word
$\alpha \in {\overrightarrow {\Sigma ^{*}}}$
, there exists a word
![]() $\gamma \in \Sigma ^{*}$
, such that
$\gamma \in \Sigma ^{*}$
, such that
![]() $\gamma \rightarrow ^{*} \alpha \equiv \beta \beta '$
. It follows from Corollary 4.10 that there exists a decomposition
$\gamma \rightarrow ^{*} \alpha \equiv \beta \beta '$
. It follows from Corollary 4.10 that there exists a decomposition
![]() $\gamma \equiv \gamma _1 \gamma _2$
with
$\gamma \equiv \gamma _1 \gamma _2$
with
![]() $\gamma _1 \rightarrow ^{*} \beta $
and
$\gamma _1 \rightarrow ^{*} \beta $
and
![]() $\gamma _2 \rightarrow ^{*} \beta '$
. Since
$\gamma _2 \rightarrow ^{*} \beta '$
. Since
![]() $\gamma \in \Sigma ^{*}$
and
$\gamma \in \Sigma ^{*}$
and
![]() $\gamma _1$
is a prefix of
$\gamma _1$
is a prefix of
![]() $\gamma $
, it follows that
$\gamma $
, it follows that
![]() $\gamma _1 \in \Sigma ^{*}$
. Since
$\gamma _1 \in \Sigma ^{*}$
. Since
![]() $\gamma _1 \in \Sigma ^{*}$
and
$\gamma _1 \in \Sigma ^{*}$
and
![]() $\gamma _1 \rightarrow ^{*} \beta $
, it follows that
$\gamma _1 \rightarrow ^{*} \beta $
, it follows that
![]() $\beta \in {\overrightarrow {\Sigma ^{*}}}$
.
$\beta \in {\overrightarrow {\Sigma ^{*}}}$
.
Note that
![]() $\Sigma ^{*}$
is closed under products.
$\Sigma ^{*}$
is closed under products.
Lemma 4.12. The set
![]() ${\overrightarrow {\Sigma ^{*}}}$
is closed under products, that is if
${\overrightarrow {\Sigma ^{*}}}$
is closed under products, that is if
![]() $\alpha \in {\overrightarrow {\Sigma ^{*}}}$
and
$\alpha \in {\overrightarrow {\Sigma ^{*}}}$
and
![]() $\beta \in {\overrightarrow {\Sigma ^{*}}}$
, then
$\beta \in {\overrightarrow {\Sigma ^{*}}}$
, then
![]() $\alpha \beta \in {\overrightarrow {\Sigma ^{*}}}$
.
$\alpha \beta \in {\overrightarrow {\Sigma ^{*}}}$
.
Proof. Let
![]() $\alpha _0, \beta _0 \in \Sigma ^{*}$
, such that
$\alpha _0, \beta _0 \in \Sigma ^{*}$
, such that
![]() $\alpha _0 \rightarrow ^{*} \alpha $
and
$\alpha _0 \rightarrow ^{*} \alpha $
and
![]() $\beta _0 \rightarrow ^{*} \beta $
. It follows that
$\beta _0 \rightarrow ^{*} \beta $
. It follows that
![]() $\alpha _0 \beta _0 \in \Sigma ^{*}$
with
$\alpha _0 \beta _0 \in \Sigma ^{*}$
with
![]() $\alpha _0\beta _0 \rightarrow \alpha \beta $
, hence,
$\alpha _0\beta _0 \rightarrow \alpha \beta $
, hence,
![]() $\alpha \beta \in {\overrightarrow {\Sigma ^{*}}}$
.
$\alpha \beta \in {\overrightarrow {\Sigma ^{*}}}$
.
Lemma 4.13. We have
![]() $r_i \in {\mathcal {U}}$
for all
$r_i \in {\mathcal {U}}$
for all
![]() $i \in I$
.
$i \in I$
.
Proof. By definition of
![]() $\Sigma $
, both
$\Sigma $
, both
![]() $r_i \in \Sigma $
and
$r_i \in \Sigma $
and
![]() $r_i^{-1} \in \Sigma $
. Since
$r_i^{-1} \in \Sigma $
. Since
![]() $\Sigma $
is a subset of
$\Sigma $
is a subset of
![]() ${\overrightarrow {\Sigma ^{*}}}$
, it follows from the definition of
${\overrightarrow {\Sigma ^{*}}}$
, it follows from the definition of
![]() ${\mathcal {U}}$
that
${\mathcal {U}}$
that
![]() $r_i \in {\mathcal {U}}$
.
$r_i \in {\mathcal {U}}$
.
The following is immediate from the definition of
![]() ${\mathcal {U}}$
.
${\mathcal {U}}$
.
Lemma 4.14. The set
![]() ${\mathcal {U}}$
is closed under inverses, that is if
${\mathcal {U}}$
is closed under inverses, that is if
![]() $\alpha \in {\mathcal {U}}$
, then
$\alpha \in {\mathcal {U}}$
, then
![]() $\alpha ^{-1} \in {\mathcal {U}}$
.
$\alpha ^{-1} \in {\mathcal {U}}$
.
Lemma 4.15. The set
![]() ${\mathcal {U}}$
is closed under products, that is if
${\mathcal {U}}$
is closed under products, that is if
![]() $\alpha \in {\mathcal {U}}$
and
$\alpha \in {\mathcal {U}}$
and
![]() $\beta \in {\mathcal {U}}$
, then
$\beta \in {\mathcal {U}}$
, then
![]() $\alpha \beta \in {\mathcal {U}}$
.
$\alpha \beta \in {\mathcal {U}}$
.
Proof. Since
![]() ${\mathcal {U}}$
is closed under inverses by Lemma 4.14, it follows that
${\mathcal {U}}$
is closed under inverses by Lemma 4.14, it follows that
![]() $\alpha , \alpha ^{-1}, \beta , \beta ^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
. But
$\alpha , \alpha ^{-1}, \beta , \beta ^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
. But
![]() ${\overrightarrow {\Sigma ^{*}}}$
is closed under products by Lemma 4.12, hence,
${\overrightarrow {\Sigma ^{*}}}$
is closed under products by Lemma 4.12, hence,
![]() $\alpha \beta \in {\overrightarrow {\Sigma ^{*}}}$
and
$\alpha \beta \in {\overrightarrow {\Sigma ^{*}}}$
and
![]() $(\alpha \beta )^{-1} \equiv \beta ^{-1} \alpha ^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
, hence,
$(\alpha \beta )^{-1} \equiv \beta ^{-1} \alpha ^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
, hence,
![]() $\alpha \beta \in {\mathcal {U}}$
by definition of
$\alpha \beta \in {\mathcal {U}}$
by definition of
![]() ${\mathcal {U}}$
.
${\mathcal {U}}$
.
Note that the set
![]() ${\mathcal {U}}$
will not in general be closed under prefixes.
${\mathcal {U}}$
will not in general be closed under prefixes.
Lemma 4.16. The set
![]() ${\mathcal {U}}$
is closed under partial free reductions, that is if
${\mathcal {U}}$
is closed under partial free reductions, that is if
![]() $\alpha \in {\mathcal {U}}$
and
$\alpha \in {\mathcal {U}}$
and
![]() $\alpha \rightarrow ^{*} \beta $
, then
$\alpha \rightarrow ^{*} \beta $
, then
![]() $\beta \in {\mathcal {U}}$
.
$\beta \in {\mathcal {U}}$
.
Proof. Since
![]() $\alpha \in {\mathcal {U}}$
, it follows from the definition of
$\alpha \in {\mathcal {U}}$
, it follows from the definition of
![]() ${\mathcal {U}}$
that
${\mathcal {U}}$
that
![]() $\alpha \in {\overrightarrow {\Sigma ^{*}}}$
and
$\alpha \in {\overrightarrow {\Sigma ^{*}}}$
and
![]() $\alpha ^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
. Since
$\alpha ^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
. Since
![]() $\alpha \rightarrow ^{*} \beta $
, it follows from the definition of
$\alpha \rightarrow ^{*} \beta $
, it follows from the definition of
![]() $\rightarrow ^{*}$
that
$\rightarrow ^{*}$
that
![]() $\alpha ^{-1} \rightarrow ^{*} \beta ^{-1}$
. Hence,
$\alpha ^{-1} \rightarrow ^{*} \beta ^{-1}$
. Hence,
![]() $\beta \in {\overrightarrow {\Sigma ^{*}}}$
and
$\beta \in {\overrightarrow {\Sigma ^{*}}}$
and
![]() $\beta ^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
. Since
$\beta ^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
. Since
![]() $\beta \in {\overrightarrow {\Sigma ^{*}}}$
and
$\beta \in {\overrightarrow {\Sigma ^{*}}}$
and
![]() $\beta ^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
, it follows from the definition of
$\beta ^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
, it follows from the definition of
![]() ${\mathcal {U}}$
that
${\mathcal {U}}$
that
![]() $\beta \in {\mathcal {U}}$
.
$\beta \in {\mathcal {U}}$
.
We are now in a position to prove the key lemma that we need to prove our main result relating the Benois algorithm and the Adjan algorithm.
Lemma 4.17. The set
![]() ${\mathcal {U}}$
is closed under the Adjan overlap algorithm, that is for all words
${\mathcal {U}}$
is closed under the Adjan overlap algorithm, that is for all words
![]() $\alpha , \beta , \gamma \in \overline {A}^{*}$
, if
$\alpha , \beta , \gamma \in \overline {A}^{*}$
, if
![]() $\alpha \beta \in {\mathcal {U}}$
and
$\alpha \beta \in {\mathcal {U}}$
and
![]() $\beta \gamma \in {\mathcal {U}}$
, then
$\beta \gamma \in {\mathcal {U}}$
, then
![]() $\{\alpha , \beta , \gamma \} \subseteq {\mathcal {U}}$
. In other words, the submonoid
$\{\alpha , \beta , \gamma \} \subseteq {\mathcal {U}}$
. In other words, the submonoid
![]() ${\mathcal {U}}$
of
${\mathcal {U}}$
of
![]() $\overline {A}^{*}$
has property (
$\overline {A}^{*}$
has property (
![]() ${\mathcal {A}}$
).
${\mathcal {A}}$
).
Proof. Since
![]() $\alpha \beta , \beta \gamma \in {\mathcal {U}}$
and
$\alpha \beta , \beta \gamma \in {\mathcal {U}}$
and
![]() ${\mathcal {U}}$
is closed under inverses by Lemma 4.14, it follows that
${\mathcal {U}}$
is closed under inverses by Lemma 4.14, it follows that
Since
![]() ${\overrightarrow {\Sigma ^{*}}}$
is prefix closed by Lemma 4.11, and
${\overrightarrow {\Sigma ^{*}}}$
is prefix closed by Lemma 4.11, and
![]() $\beta ^{-1}\alpha ^{-1}, \beta \gamma \in {\overrightarrow {\Sigma ^{*}}}$
, it follows that
$\beta ^{-1}\alpha ^{-1}, \beta \gamma \in {\overrightarrow {\Sigma ^{*}}}$
, it follows that
![]() $\beta ^{-1}, \beta \in {\overrightarrow {\Sigma ^{*}}}$
, which implies
$\beta ^{-1}, \beta \in {\overrightarrow {\Sigma ^{*}}}$
, which implies
![]() $\beta \in {\mathcal {U}}$
and
$\beta \in {\mathcal {U}}$
and
![]() $\beta ^{-1} \in {\mathcal {U}}$
. Since
$\beta ^{-1} \in {\mathcal {U}}$
. Since
![]() ${\mathcal {U}}$
is closed for products by Lemma 4.15, and
${\mathcal {U}}$
is closed for products by Lemma 4.15, and
![]() $\beta ^{-1} \in {\mathcal {U}}$
and
$\beta ^{-1} \in {\mathcal {U}}$
and
![]() $\beta \gamma \in {\mathcal {U}}$
, it follows that
$\beta \gamma \in {\mathcal {U}}$
, it follows that
![]() $\beta ^{-1}\beta \gamma \in {\mathcal {U}}$
, and hence,
$\beta ^{-1}\beta \gamma \in {\mathcal {U}}$
, and hence,
![]() $\gamma \in {\mathcal {U}}$
since
$\gamma \in {\mathcal {U}}$
since
![]() ${\mathcal {U}}$
is closed under partial free reductions by Lemma 4.16.
${\mathcal {U}}$
is closed under partial free reductions by Lemma 4.16.
Also,
![]() $\alpha \beta \in {\mathcal {U}}$
and
$\alpha \beta \in {\mathcal {U}}$
and
![]() $\beta ^{-1} \in {\mathcal {U}}$
implies
$\beta ^{-1} \in {\mathcal {U}}$
implies
![]() $\alpha \beta \beta ^{-1} \in {\mathcal {U}}$
by Lemma 4.15, which thus
$\alpha \beta \beta ^{-1} \in {\mathcal {U}}$
by Lemma 4.15, which thus
![]() $\alpha \in {\mathcal {U}}$
by Lemma 4.16.
$\alpha \in {\mathcal {U}}$
by Lemma 4.16.
This completes the proof that
![]() $\{\alpha , \beta , \gamma \} \subseteq {\mathcal {U}}$
.
$\{\alpha , \beta , \gamma \} \subseteq {\mathcal {U}}$
.
We now have all we need to prove our main result of this section.
Proof of Theorem 4.5
Let p be some prefix of some relator
![]() $r_i$
, with
$r_i$
, with
![]() $i \in I$
. Write
$i \in I$
. Write
![]() $r_i \equiv pq$
. Suppose p is an invertible prefix of
$r_i \equiv pq$
. Suppose p is an invertible prefix of
![]() $r_i$
computed by the Adjan algorithm. By definition of the Adjan algorithm, this means that p belongs to the submonoid
$r_i$
computed by the Adjan algorithm. By definition of the Adjan algorithm, this means that p belongs to the submonoid
![]() $U(R)$
of
$U(R)$
of
![]() $\overline {A}^{*}$
generated by the finite biprefix code
$\overline {A}^{*}$
generated by the finite biprefix code
![]() $B(R)$
computed by the Adjan algorithm, where
$B(R)$
computed by the Adjan algorithm, where
![]() $R = \{r_i \::\: i \in I \}$
. Since
$R = \{r_i \::\: i \in I \}$
. Since
![]() $r_i \in {\mathcal {U}}$
for all
$r_i \in {\mathcal {U}}$
for all
![]() $i \in I$
by Lemma 4.13 and
$i \in I$
by Lemma 4.13 and
![]() ${\mathcal {U}}$
is closed under the Adjan algorithm by Lemma 4.17, it follows that
${\mathcal {U}}$
is closed under the Adjan algorithm by Lemma 4.17, it follows that
![]() ${\mathcal {U}}$
is a submonoid of
${\mathcal {U}}$
is a submonoid of
![]() $\overline {A}^{*}$
with
$\overline {A}^{*}$
with
![]() $R \subseteq {\mathcal {U}}$
and
$R \subseteq {\mathcal {U}}$
and
![]() ${\mathcal {U}}$
has property (
${\mathcal {U}}$
has property (
![]() ${\mathcal {A}}$
). By definition,
${\mathcal {A}}$
). By definition,
![]() $U(R)$
is the smallest submonoid of
$U(R)$
is the smallest submonoid of
![]() $\overline {A}^{*}$
, such that
$\overline {A}^{*}$
, such that
![]() $R \subseteq U(R)$
and
$R \subseteq U(R)$
and
![]() $U(R)$
satisfies (
$U(R)$
satisfies (
![]() ${\mathcal {A}}$
). Hence, it follows that
${\mathcal {A}}$
). Hence, it follows that
![]() $U(R) \subseteq {\mathcal {U}}$
. Since p belongs to
$U(R) \subseteq {\mathcal {U}}$
. Since p belongs to
![]() $U(R)$
by assumption, it follows that p also belongs to
$U(R)$
by assumption, it follows that p also belongs to
![]() ${\mathcal {U}}$
. But then by Lemma 4.7, since
${\mathcal {U}}$
. But then by Lemma 4.7, since
![]() $p \in {\mathcal {U}}$
, it follows that p is an invertible prefix of a relator (specifically of the relator
$p \in {\mathcal {U}}$
, it follows that p is an invertible prefix of a relator (specifically of the relator
![]() $r_i$
) computed by the Benois algorithm.
$r_i$
) computed by the Benois algorithm.
Definition 4.18. We call a set of words
![]() $W \subseteq X^{*}$
overlap free, if for all
$W \subseteq X^{*}$
overlap free, if for all
![]() $w_1, w_2 \in W$
, we have
$w_1, w_2 \in W$
, we have
 $$\begin{align*}\mathrm{pref}(w_1) \cap \mathrm{suff}(w_2) = \begin{cases} \{ \epsilon \} & \mbox{if } w_1 \neq w_2 \\ \{ \epsilon, w_1 \} & \mbox{if } w_1 = w_2. \end{cases} \end{align*}$$
$$\begin{align*}\mathrm{pref}(w_1) \cap \mathrm{suff}(w_2) = \begin{cases} \{ \epsilon \} & \mbox{if } w_1 \neq w_2 \\ \{ \epsilon, w_1 \} & \mbox{if } w_1 = w_2. \end{cases} \end{align*}$$
Definition 4.19. We call a set
![]() $W \subseteq \overline {A}^{*}$
i-overlap free if
$W \subseteq \overline {A}^{*}$
i-overlap free if
![]() $W \cup W^{-1}$
is overlap free.
$W \cup W^{-1}$
is overlap free.
Remark 4.20. It is not clear (and possibly not true in general) that the set of Benois pieces is i-overlap free. However, it is a consequence of the results above that if all the relators
![]() $r_i \; (i \in I)$
are reduced words, then the Benois pieces are all i-overlap free. To see this, suppose that p is a prefix of
$r_i \; (i \in I)$
are reduced words, then the Benois pieces are all i-overlap free. To see this, suppose that p is a prefix of
![]() $r_i$
with
$r_i$
with
![]() $p \in V$
and
$p \in V$
and
![]() $\operatorname {\mathrm {red}}(p^{-1}) \in V$
(i.e. p is computed by the Benois algorithm). Since p is a reduced word, it follows that
$\operatorname {\mathrm {red}}(p^{-1}) \in V$
(i.e. p is computed by the Benois algorithm). Since p is a reduced word, it follows that
![]() $p^{-1}$
is also reduced, so
$p^{-1}$
is also reduced, so
![]() $p^{-1} \equiv \operatorname {\mathrm {red}}(p^{-1}) \in V$
. So we have both
$p^{-1} \equiv \operatorname {\mathrm {red}}(p^{-1}) \in V$
. So we have both
![]() $p \in V$
and
$p \in V$
and
![]() $p^{-1} \in V$
, where
$p^{-1} \in V$
, where
![]() $V = \operatorname {\mathrm {red}}(\Sigma ^{*}) \subseteq {\overrightarrow {\Sigma ^{*}}}$
. Since
$V = \operatorname {\mathrm {red}}(\Sigma ^{*}) \subseteq {\overrightarrow {\Sigma ^{*}}}$
. Since
![]() $p \in {\overrightarrow {\Sigma ^{*}}}$
and
$p \in {\overrightarrow {\Sigma ^{*}}}$
and
![]() $p^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
, it follows from the definition of
$p^{-1} \in {\overrightarrow {\Sigma ^{*}}}$
, it follows from the definition of
![]() ${\mathcal {U}}$
that
${\mathcal {U}}$
that
![]() $p \in {\mathcal {U}}$
. It then follows by Lemma 4.17 that when all the relators
$p \in {\mathcal {U}}$
. It then follows by Lemma 4.17 that when all the relators
![]() $r_i$
are reduced words, all the pieces of relators computed by the Benois algorithm also belong to the set
$r_i$
are reduced words, all the pieces of relators computed by the Benois algorithm also belong to the set
![]() ${\mathcal {U}}$
. But then since
${\mathcal {U}}$
. But then since
![]() ${\mathcal {U}}$
is closed under taking inverses by Lemma 4.14, it follows from Lemma 4.17 that the set pieces of the relators computed by the Benois algorithm is i-overlap free.
${\mathcal {U}}$
is closed under taking inverses by Lemma 4.14, it follows from Lemma 4.17 that the set pieces of the relators computed by the Benois algorithm is i-overlap free.
Example 4.21. We now illustrate the Benois algorithm by applying it to the O’Hare monoid
We claim that when applied to this example, the Benois algorithm will compute the following decomposition of r into invertible pieces
For notational convenience, we set
Using the same notation as above, we have
and
![]() $V = \mathrm {red}(\Sigma ^{*})$
, which is a subset of
$V = \mathrm {red}(\Sigma ^{*})$
, which is a subset of
![]() $F_A$
. Since r is a positive word, it follows that for every prefix p of r, both p and
$F_A$
. Since r is a positive word, it follows that for every prefix p of r, both p and
![]() $p^{-1}$
are reduced words. It follows that the Benois algorithm will compute the set of all prefixes p of r, such that
$p^{-1}$
are reduced words. It follows that the Benois algorithm will compute the set of all prefixes p of r, such that
![]() $p^{-1} \in V$
.
$p^{-1} \in V$
.
Let us now list some of the prefixes p that this algorithm will compute. It is a straightforward calculation to verify that
and
Then, we have:
 $$ \begin{align*} \alpha^{-1} &\equiv \operatorname{\mathrm{red}}(\beta^{-1} \alpha \delta^{-1} ) \equiv \operatorname{\mathrm{red}}( \; \beta^{-1} \cdot \alpha \beta \cdot (\alpha\beta\gamma\delta\beta)^{-1} \cdot (\alpha\beta\gamma) \; ) \in V \\ (\alpha \beta)^{-1} &\equiv \beta^{-1} \alpha^{-1} \equiv \operatorname{\mathrm{red}}(\; \beta^{-1} \beta^{-1} \alpha \delta^{-1} \;) \equiv \operatorname{\mathrm{red}}(\; \beta^{-1} \cdot \beta^{-1} \cdot \alpha \beta \cdot (\alpha\beta\gamma\delta\beta)^{-1} \cdot (\alpha\beta\gamma) \;) \in V \\ (\alpha \beta \gamma)^{-1} &\equiv \operatorname{\mathrm{red}}( (\delta \beta) (\alpha \beta \gamma \delta \beta)^{-1} ) \equiv \operatorname{\mathrm{red}}( (\alpha \beta^{-1} \alpha) \beta (\alpha \beta \gamma \delta \beta)^{-1} ) \\ &\equiv \operatorname{\mathrm{red}}( \alpha \cdot \beta^{-1} \cdot \alpha \beta \cdot (\alpha \beta \gamma \delta \beta)^{-1} ) \in V \\ (\alpha \beta \gamma \delta)^{-1} &= \operatorname{\mathrm{red}}(\beta (\alpha \beta \gamma \delta \beta)^{-1}) = \operatorname{\mathrm{red}}( \alpha \delta^{-1} \alpha (\alpha \beta \gamma \delta \beta)^{-1} ) \\ &= \operatorname{\mathrm{red}}( (\alpha \beta) \cdot (\delta \beta)^{-1} \cdot \alpha \cdot (\alpha \beta \gamma \delta \beta)^{-1} ) \in V. \end{align*} $$
$$ \begin{align*} \alpha^{-1} &\equiv \operatorname{\mathrm{red}}(\beta^{-1} \alpha \delta^{-1} ) \equiv \operatorname{\mathrm{red}}( \; \beta^{-1} \cdot \alpha \beta \cdot (\alpha\beta\gamma\delta\beta)^{-1} \cdot (\alpha\beta\gamma) \; ) \in V \\ (\alpha \beta)^{-1} &\equiv \beta^{-1} \alpha^{-1} \equiv \operatorname{\mathrm{red}}(\; \beta^{-1} \beta^{-1} \alpha \delta^{-1} \;) \equiv \operatorname{\mathrm{red}}(\; \beta^{-1} \cdot \beta^{-1} \cdot \alpha \beta \cdot (\alpha\beta\gamma\delta\beta)^{-1} \cdot (\alpha\beta\gamma) \;) \in V \\ (\alpha \beta \gamma)^{-1} &\equiv \operatorname{\mathrm{red}}( (\delta \beta) (\alpha \beta \gamma \delta \beta)^{-1} ) \equiv \operatorname{\mathrm{red}}( (\alpha \beta^{-1} \alpha) \beta (\alpha \beta \gamma \delta \beta)^{-1} ) \\ &\equiv \operatorname{\mathrm{red}}( \alpha \cdot \beta^{-1} \cdot \alpha \beta \cdot (\alpha \beta \gamma \delta \beta)^{-1} ) \in V \\ (\alpha \beta \gamma \delta)^{-1} &= \operatorname{\mathrm{red}}(\beta (\alpha \beta \gamma \delta \beta)^{-1}) = \operatorname{\mathrm{red}}( \alpha \delta^{-1} \alpha (\alpha \beta \gamma \delta \beta)^{-1} ) \\ &= \operatorname{\mathrm{red}}( (\alpha \beta) \cdot (\delta \beta)^{-1} \cdot \alpha \cdot (\alpha \beta \gamma \delta \beta)^{-1} ) \in V. \end{align*} $$
This proves that the Benois algorithm computes a decomposition which is a refinement of the above decomposition. To show that it is exactly this decomposition that is computed, it may be shown, by appealing to bicyclic monoid homomorphic images of this monoid, that none of the pieces of this decomposition has a proper nonempty invertible prefix. Indeed, if there were a finer decomposition into minimal invertible pieces, then one quickly sees that in all possible cases, this would imply that all the generators are invertible, and so the monoid
![]() ${\mathcal {O}}$
would need to be a group. However,
${\mathcal {O}}$
would need to be a group. However,
![]() ${\mathcal {O}}$
is not a group since the map from
${\mathcal {O}}$
is not a group since the map from
![]() $\{a,b,c,d\}^{*}$
onto
$\{a,b,c,d\}^{*}$
onto
![]() $\{x,y\}^{*}$
defined by
$\{x,y\}^{*}$
defined by
![]() $a \mapsto a$
,
$a \mapsto a$
,
![]() $b \mapsto 1$
,
$b \mapsto 1$
,
![]() $c \mapsto 1$
and
$c \mapsto 1$
and
![]() $d \mapsto d$
induces a surjective a homomorphism from
$d \mapsto d$
induces a surjective a homomorphism from
![]() ${\mathcal {O}}$
onto the bicyclic monoid
${\mathcal {O}}$
onto the bicyclic monoid
![]() ${\operatorname {Inv}\bigl \langle {a,d}\:|\:{ad=1} \bigr \rangle }$
.
${\operatorname {Inv}\bigl \langle {a,d}\:|\:{ad=1} \bigr \rangle }$
.
We leave the details of this as an exercise for the reader.
5 Examples
This section will contain some examples of one-relator groups, and one-relator inverse monoids, to which the results of the previous sections can be applied. We have already seen some applications in Section 3, for example to the case where the pieces
![]() $p_i$
are powers of generators from A (see (F1) in Section 3).
$p_i$
are powers of generators from A (see (F1) in Section 3).
We are motivated by the question of whether the group of units of a one-relator inverse monoid is a one-relator group. Recall that at the start of Section 3, we gave the example of the one-relator inverse monoid
with minimal invertible pieces a,
![]() $bc^2b^{-1}$
, and
$bc^2b^{-1}$
, and
![]() $bc^{3}b^{-1}$
. We observed there that
$bc^{3}b^{-1}$
. We observed there that
is not a presentation for the group of units of the monoid M. A key feature of that example was that
![]() $\{a,bc^2b^{-1},bc^3b^{-1}\}$
is not a basis for
$\{a,bc^2b^{-1},bc^3b^{-1}\}$
is not a basis for
![]() ${\operatorname {Gp}\bigl \langle {a,bc^2b^{-1},bc^3b^{-1}} \bigr \rangle }\leq F_{a,b,c}$
. On the other hand,
${\operatorname {Gp}\bigl \langle {a,bc^2b^{-1},bc^3b^{-1}} \bigr \rangle }\leq F_{a,b,c}$
. On the other hand,
![]() $\{a, bcb^{-1} \}$
is a basis for
$\{a, bcb^{-1} \}$
is a basis for
![]() ${\operatorname {Gp}\bigl \langle {a,bc^2b^{-1},bc^3b^{-1}} \bigr \rangle }\leq F_{a,b,c}$
, and this basis satisfies the conditions of Theorem 3.11 (setting
${\operatorname {Gp}\bigl \langle {a,bc^2b^{-1},bc^3b^{-1}} \bigr \rangle }\leq F_{a,b,c}$
, and this basis satisfies the conditions of Theorem 3.11 (setting
![]() $\mu (a)=a$
and
$\mu (a)=a$
and
![]() $\mu (bcb^{-1})=c$
). Using this fact, we can express each of the original pieces
$\mu (bcb^{-1})=c$
). Using this fact, we can express each of the original pieces
![]() $\{a,bc^2b^{-1},bc^3b^{-1}\}$
in terms of the basis
$\{a,bc^2b^{-1},bc^3b^{-1}\}$
in terms of the basis
![]() $\{a, bcb^{-1} \}$
, which rewrites the relator word
$\{a, bcb^{-1} \}$
, which rewrites the relator word
as
and then by Corollary 3.13, we can conclude that the group of units of M is the one-relator group with presentation
It is natural to ask whether this approach might be used for other one-relator inverse monoids. As explained in the Introduction, one of the key motivating examples for the work is the O’Hare monoid. We shall now show how the group of units of the O’Hare monoid can indeed be computed using a similar approach to the example above.
5.1 The group of units of the O’Hare monoid
Recall from the Introduction that the O’Hare monoid
![]() ${\mathcal {O}}$
is the inverse monoid defined by the following inverse monoid presentation
${\mathcal {O}}$
is the inverse monoid defined by the following inverse monoid presentation
As explained in the Introduction, this was one of the main motivating examples which prompted the research presented in this paper. As already mentioned above, Margolis et al. [Reference Margolis, Meakin and Stephen22] proved that the decomposition into minimal invertible pieces of this defining relator is
They prove this using van Kampen diagrams and Stephen’s procedure. We gave an alternative proof of this fact in Example 4.21 using the Benois algorithm (see Lemma 4.4). As in Example 4.21, for notational convenience, we set
We shall now show how the results from Section 3 can be applied to prove that the group of units
![]() $U({\mathcal {O}})$
of the O’Hare monoid
$U({\mathcal {O}})$
of the O’Hare monoid
![]() ${\mathcal {O}}$
is the free group of rank
${\mathcal {O}}$
is the free group of rank
![]() $2$
.
$2$
.
This is interesting for two reasons. Firstly, it shows that the groups of units of the O’Hare monoid
![]() ${\mathcal {O}}$
is a one-relator group (since every free group is vacuously a one-relator group). Secondly, while the group of units of
${\mathcal {O}}$
is a one-relator group (since every free group is vacuously a one-relator group). Secondly, while the group of units of
![]() ${\mathcal {O}}$
is a one-relator group, the group of units is not isomorphic to the group
${\mathcal {O}}$
is a one-relator group, the group of units is not isomorphic to the group
which is the presentation obtained by replacing each minimal invertible piece by a letter in the obvious way. Indeed, in the presentation for H, we can remove the redundant generator
![]() $\delta $
, and so H is the free group on
$\delta $
, and so H is the free group on
![]() $\{\alpha ,\beta ,\gamma \}$
.
$\{\alpha ,\beta ,\gamma \}$
.
This gives another example (in addition to the example discussed at the start of Section 3) showing that Makanin’s theorem for special monoids (Theorem 1.2) does not generalise directly to special inverse monoids. We will construct further examples later in this paper which show just how dramatically Makanin’s theorem fails to generalise to special inverse monoids.
So we are left with the task of proving that the group of units
![]() $U({\mathcal {O}})$
of
$U({\mathcal {O}})$
of
![]() ${\mathcal {O}}$
is a free group of rank
${\mathcal {O}}$
is a free group of rank
![]() $2$
.
$2$
.
The first step will be to write down an alternative one-relator presentation for
![]() ${\mathcal {O}}$
which has minimal invertible pieces that satisfy condition (F3) from Section 3.
${\mathcal {O}}$
which has minimal invertible pieces that satisfy condition (F3) from Section 3.
Since
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
,
$\beta $
,
![]() $\gamma $
and
$\gamma $
and
![]() $\delta $
all represent invertible elements of the monoid
$\delta $
all represent invertible elements of the monoid
![]() ${\mathcal {O}}$
, it follows that
${\mathcal {O}}$
, it follows that
and
are both invertible in
![]() ${\mathcal {O}}$
. Hence, by Lemma 2.2, it follows that these words are equal in
${\mathcal {O}}$
. Hence, by Lemma 2.2, it follows that these words are equal in
![]() ${\mathcal {O}}$
to the words obtained by freely reducing them, namely, the words
${\mathcal {O}}$
to the words obtained by freely reducing them, namely, the words
![]() $aba^{-1}$
and
$aba^{-1}$
and
![]() $aca^{-1}$
. This shows that
$aca^{-1}$
. This shows that
are all invertible in
![]() ${\mathcal {O}}$
. It follows that any product of these words is also invertible in
${\mathcal {O}}$
. It follows that any product of these words is also invertible in
![]() ${\mathcal {O}}$
. In particular, the word
${\mathcal {O}}$
. In particular, the word
is invertible in
![]() ${\mathcal {O}}$
. Since this word is invertible, it follows from Lemma 2.2 that it is equal in
${\mathcal {O}}$
. Since this word is invertible, it follows from Lemma 2.2 that it is equal in
![]() ${\mathcal {O}}$
to the word obtained by freely reducing this word. But it is easy to see that the free reduction of this word gives the defining relator r in the original presentation for
${\mathcal {O}}$
to the word obtained by freely reducing this word. But it is easy to see that the free reduction of this word gives the defining relator r in the original presentation for
![]() ${\mathcal {O}}$
. Hence,
${\mathcal {O}}$
. Hence,
![]() $u = r = 1$
holds in the monoid
$u = r = 1$
holds in the monoid
![]() ${\mathcal {O}}$
.
${\mathcal {O}}$
.
Conversely, let M be the inverse monoid defined by the presentation
where u is the word above. Since u is invertible in M, it follows that
![]() $u = \mathrm {red}(u)$
in M. Hence,
$u = \mathrm {red}(u)$
in M. Hence,
![]() $u=r$
in M.
$u=r$
in M.
Combining these observations, we have proved
So the O’Hare monoid is defined by the presentation
Next, we claim that working with this new presentation for
![]() ${\mathcal {O}}$
, the minimal invertible pieces of the defining relator u are
${\mathcal {O}}$
, the minimal invertible pieces of the defining relator u are
![]() $aba^{-1}$
,
$aba^{-1}$
,
![]() $aca^{-1}$
and
$aca^{-1}$
and
![]() $ad$
. We already proved above that each of these words represents an invertible element of
$ad$
. We already proved above that each of these words represents an invertible element of
![]() ${\mathcal {O}}$
, so these are certainly invertible pieces of the defining relator u. For minimality, if any of these pieces was not a minimal invertible piece, then in all cases, it would follow that a is invertible. But a is not invertible in
${\mathcal {O}}$
, so these are certainly invertible pieces of the defining relator u. For minimality, if any of these pieces was not a minimal invertible piece, then in all cases, it would follow that a is invertible. But a is not invertible in
![]() ${\mathcal {O}}$
since
${\mathcal {O}}$
since
![]() $ad$
is a minimal invertible piece of r.
$ad$
is a minimal invertible piece of r.
We claim that the decomposition of u into minimal invertible pieces in the presentation
![]() ${\operatorname {Inv}\bigl \langle {a,b,c,d}\:|\:{u=1} \bigr \rangle }$
satisfies condition (F3) from Section 3. For this, we just need to observe that each piece contains a letter which appears in that piece exactly once, and does not appear in any of the other pieces. Here, we can take b in the piece
${\operatorname {Inv}\bigl \langle {a,b,c,d}\:|\:{u=1} \bigr \rangle }$
satisfies condition (F3) from Section 3. For this, we just need to observe that each piece contains a letter which appears in that piece exactly once, and does not appear in any of the other pieces. Here, we can take b in the piece
![]() $aba^{-1}$
, c in the piece
$aba^{-1}$
, c in the piece
![]() $aca^{-1}$
and the letter d in the piece
$aca^{-1}$
and the letter d in the piece
![]() $ad$
.
$ad$
.
Since condition (F3) holds, it follows that the hypotheses of Corollary 3.13 are satisfied, and hence, applying this corollary, we conclude that the group of units
![]() $U({\mathcal {O}})$
of
$U({\mathcal {O}})$
of
![]() ${\mathcal {O}}$
is isomorphic to
${\mathcal {O}}$
is isomorphic to
Comparing this with the example at the start of Section 3, what we have proved here is that the situation with the O’Hare monoid is similar. Indeed, the original set of pieces
![]() $\{abcd, acd, ad, abbcd \}$
is not a basis for
$\{abcd, acd, ad, abbcd \}$
is not a basis for
![]() ${\operatorname {Gp}\bigl \langle {abcd, acd, ad, abbcd } \bigr \rangle } \leq F_{a,b,c,d}$
. On the other hand,
${\operatorname {Gp}\bigl \langle {abcd, acd, ad, abbcd } \bigr \rangle } \leq F_{a,b,c,d}$
. On the other hand,
![]() $\{aba^{-1}, aca^{-1}, ad \}$
is a basis for
$\{aba^{-1}, aca^{-1}, ad \}$
is a basis for
![]() ${\operatorname {Gp}\bigl \langle {abcd, acd, ad, abbcd } \bigr \rangle }\leq F_{a,b,c,d}$
, and this basis satisfies the conditions of Theorem 3.11 (setting
${\operatorname {Gp}\bigl \langle {abcd, acd, ad, abbcd } \bigr \rangle }\leq F_{a,b,c,d}$
, and this basis satisfies the conditions of Theorem 3.11 (setting
![]() $\mu (aba^{-1})=b$
,
$\mu (aba^{-1})=b$
,
![]() $\mu (aca^{-1})=c$
and
$\mu (aca^{-1})=c$
and
![]() $\mu (ad)=d$
). If we rewrite the pieces in the original O’Hare presentation in terms of this basis and then apply Corollary 3.13, we conclude (via the calculations above) that the group of units of
$\mu (ad)=d$
). If we rewrite the pieces in the original O’Hare presentation in terms of this basis and then apply Corollary 3.13, we conclude (via the calculations above) that the group of units of
![]() ${\mathcal {O}}$
is isomorphic to the one-relator group
${\mathcal {O}}$
is isomorphic to the one-relator group
![]() ${\operatorname {Gp}\bigl \langle {x,y,z}\:|\:{xyzyzzxxyzyz=1} \bigr \rangle }$
.
${\operatorname {Gp}\bigl \langle {x,y,z}\:|\:{xyzyzzxxyzyz=1} \bigr \rangle }$
.
Now, we have
 $$ \begin{align*} {\operatorname{Gp}\bigl\langle {x,y,z}\:|\:{xyzyzzxxyzyz=1} \bigr\rangle} & = {\operatorname{Gp}\bigl\langle {x,y,z,t}\:|\:{xttzxxtt=1, t=yz} \bigr\rangle} \\ & = {\operatorname{Gp}\bigl\langle {x,y,z,t}\:|\:{xttzxxtt=1, y=tz^{-1}} \bigr\rangle} \\ & = {\operatorname{Gp}\bigl\langle {x,z,t}\:|\:{xttzxxtt=1} \bigr\rangle} \cong \mathrm{FG}(x,t). \end{align*} $$
$$ \begin{align*} {\operatorname{Gp}\bigl\langle {x,y,z}\:|\:{xyzyzzxxyzyz=1} \bigr\rangle} & = {\operatorname{Gp}\bigl\langle {x,y,z,t}\:|\:{xttzxxtt=1, t=yz} \bigr\rangle} \\ & = {\operatorname{Gp}\bigl\langle {x,y,z,t}\:|\:{xttzxxtt=1, y=tz^{-1}} \bigr\rangle} \\ & = {\operatorname{Gp}\bigl\langle {x,z,t}\:|\:{xttzxxtt=1} \bigr\rangle} \cong \mathrm{FG}(x,t). \end{align*} $$
The last isomorphism follows upon removing the redundant generator z in the previous presentation. This completes the proof that the group of units of the O’Hare monoid is a free group of rank
![]() $2$
.
$2$
.
Both the O’Hare monoid and the example at the start of Section 3 are examples of one-relator inverse monoids
which show that the obvious generalisation of Makanin’s theorem to special one-relator monoids does not hold. However, for both these examples, it was possible to resolve the issue by finding a suitable basis for the subgroup of
![]() $F_A$
generated by the pieces of r and then rewriting each of the pieces, and the relator r, in terms of this new basis. In both cases, this gave us a one-relator presentation for the group of units of the inverse monoid in question. Specifically, these examples do not resolve the question of whether the group of units of a special one-relator inverse monoid is a one-relator group. Given these examples, it is natural to ask whether in fact the key property that we need for a set of pieces to be free for substitutions is that they are a basis for the subgroup of
$F_A$
generated by the pieces of r and then rewriting each of the pieces, and the relator r, in terms of this new basis. In both cases, this gave us a one-relator presentation for the group of units of the inverse monoid in question. Specifically, these examples do not resolve the question of whether the group of units of a special one-relator inverse monoid is a one-relator group. Given these examples, it is natural to ask whether in fact the key property that we need for a set of pieces to be free for substitutions is that they are a basis for the subgroup of
![]() $F_A$
that they generate (like in these two examples). The following example which was originally due to Higman shows that this is not the case. Specifically, it shows that the conditions in the theorems in Section 3 cannot be weakened to just insisting that the set of pieces is Nielsen reduced.
$F_A$
that they generate (like in these two examples). The following example which was originally due to Higman shows that this is not the case. Specifically, it shows that the conditions in the theorems in Section 3 cannot be weakened to just insisting that the set of pieces is Nielsen reduced.
5.2 The G. Higman example
This example appears in the following paper of Steve Pride [Reference Pride24], where he attributes the example to Graham Higman. As explained there, if we let
then the subgroup
![]() ${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle } \leq B$
is not free and every presentation of the group
${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle } \leq B$
is not free and every presentation of the group
![]() ${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
with respect to the generating set
${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
with respect to the generating set
![]() $\{a^4, b\}$
requires at least two relators. Note, the group B is the well-known Baumslag-Solitar group
$\{a^4, b\}$
requires at least two relators. Note, the group B is the well-known Baumslag-Solitar group
![]() $BS(2,3)$
.
$BS(2,3)$
.
This example arose as part of an investigation by Pride of conditions under which subgroups of one-relator groups are again one-relator. One interesting thing in this example is that the two-generated subgroup
![]() ${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
of the one-relator group B does not admit a one-relator presentation with respect to the generators
${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
of the one-relator group B does not admit a one-relator presentation with respect to the generators
![]() $\{a^4, b\}$
(as proved by Higman). On the other hand, the subgroup
$\{a^4, b\}$
(as proved by Higman). On the other hand, the subgroup
![]() ${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
is actually a one-relator group. Indeed, it may be shown that
${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
is actually a one-relator group. Indeed, it may be shown that
![]() ${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle } = B$
, that is,
${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle } = B$
, that is,
![]() $\{a^4,b\}$
is a generating set for B. To see this, it suffices to observe that in B, we have
$\{a^4,b\}$
is a generating set for B. To see this, it suffices to observe that in B, we have
But now since
![]() $a^2$
and b both belong to
$a^2$
and b both belong to
![]() ${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
, it follows that
${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
, it follows that
![]() $a^3 = b^{-1} a^2 b \in {\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
, and finally, since
$a^3 = b^{-1} a^2 b \in {\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
, and finally, since
![]() $a^3$
and
$a^3$
and
![]() $a^2$
both belong to
$a^2$
both belong to
![]() ${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
, it follows that
${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
, it follows that
![]() $a = (a^3)(a^2)^{-1}$
also belongs to
$a = (a^3)(a^2)^{-1}$
also belongs to
![]() ${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
. Hence,
${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle }$
. Hence,
![]() ${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle } = {\operatorname {Gp}\bigl \langle {a,b} \bigr \rangle } = B$
. So this is a concrete example showing that a two-generated one-relator group can admit a one-relator presentation with respect to a generating set of size two, but not admit any one-relator presentation with respect to another generating set of size two. Among other things, this shows how sensitive the property of being one-relator is to the choice of finite generating set for the group.
${\operatorname {Gp}\bigl \langle {a^4,b} \bigr \rangle } = {\operatorname {Gp}\bigl \langle {a,b} \bigr \rangle } = B$
. So this is a concrete example showing that a two-generated one-relator group can admit a one-relator presentation with respect to a generating set of size two, but not admit any one-relator presentation with respect to another generating set of size two. Among other things, this shows how sensitive the property of being one-relator is to the choice of finite generating set for the group.
The following result shows how this example can be adapted to give an example of a Nielsen reduced set which is not free for substitutions into one-relator groups. We shall not need the definition of Nielsen reduced here. The definition can be found in [Reference Lyndon and Schupp18, page 6]. The thing that is relevant for us here is the result (see [Reference Lyndon and Schupp18, Proposition 2.6]) that if
![]() $X \subseteq F_A$
is Nielsen reduced, then
$X \subseteq F_A$
is Nielsen reduced, then
![]() ${\operatorname {Gp}\bigl \langle {X} \bigr \rangle } \leq F_A$
is free with basis X.
${\operatorname {Gp}\bigl \langle {X} \bigr \rangle } \leq F_A$
is free with basis X.
Proposition 5.1. Let
![]() $X = \{ ab^{-1}a^2, b, a^{4} \}$
, which is Nielsen reduced a subset of the free group
$X = \{ ab^{-1}a^2, b, a^{4} \}$
, which is Nielsen reduced a subset of the free group
![]() $F_{a,b}$
. Let
$F_{a,b}$
. Let
![]() $\phi : F_{x,y,z} \rightarrow F_{a,b}$
be the unique homomorphism extending
$\phi : F_{x,y,z} \rightarrow F_{a,b}$
be the unique homomorphism extending
Set
and
Let
![]() $\hat {\phi }: K \rightarrow G$
be the homomorphism induced by
$\hat {\phi }: K \rightarrow G$
be the homomorphism induced by
![]() $\phi $
. Then
$\phi $
. Then
![]() $\hat {\phi }$
is not injective, and hence is not an isomorphism between K and the subgroup H of G generated by the set
$\hat {\phi }$
is not injective, and hence is not an isomorphism between K and the subgroup H of G generated by the set
![]() $X = \{ ab^{-1}a^2, b, a^{4} \}$
. That is, the Nielsen reduced set
$X = \{ ab^{-1}a^2, b, a^{4} \}$
. That is, the Nielsen reduced set
![]() $X = \{ ab^{-1}a^2, b, a^{4} \}$
is not free for substitution into the one-relator group
$X = \{ ab^{-1}a^2, b, a^{4} \}$
is not free for substitution into the one-relator group
![]() ${\operatorname {Gp}\bigl \langle {x,y,z}\:|\:{xyz^{-1}=1} \bigr \rangle }$
via
${\operatorname {Gp}\bigl \langle {x,y,z}\:|\:{xyz^{-1}=1} \bigr \rangle }$
via
![]() $x \mapsto ab^{-1}a^2, y \mapsto b$
and
$x \mapsto ab^{-1}a^2, y \mapsto b$
and
![]() $z \mapsto a^{4}$
.
$z \mapsto a^{4}$
.
Proof. It is a straightforward exercise to check that X is a Nielsen reduced set of reduced words in the free group
![]() $F_{a,b}$
, and hence,
$F_{a,b}$
, and hence,
![]() ${\operatorname {Gp}\bigl \langle {X} \bigr \rangle } \leq F_{a,b}$
is freely generated by X. Certainly,
${\operatorname {Gp}\bigl \langle {X} \bigr \rangle } \leq F_{a,b}$
is freely generated by X. Certainly,
![]() $\phi $
defines a homomorphism since
$\phi $
defines a homomorphism since
![]() $\phi (xyz^{-1})=1$
in G. Clearly, K is isomorphic to the free group on y and z. In particular, the words
$\phi (xyz^{-1})=1$
in G. Clearly, K is isomorphic to the free group on y and z. In particular, the words
![]() $z^2 y$
and
$z^2 y$
and
![]() $yz^3$
represent distinct elements in the group K. On the other hand
$yz^3$
represent distinct elements in the group K. On the other hand
in G. Indeed, in G, we have
![]() $a^2b=ba^3$
, and hence
$a^2b=ba^3$
, and hence
as required.
Note that as it stands, the example in Proposition 5.1 does not immediately give a special inverse monoid with interesting properties, since the set
![]() $X = \{ ab^{-1}a^2, b, a^{4} \}$
cannot be the set of minimal invertible words in an inverse monoid presentation (since, for instance,
$X = \{ ab^{-1}a^2, b, a^{4} \}$
cannot be the set of minimal invertible words in an inverse monoid presentation (since, for instance,
![]() $a^4$
invertible implies a is invertible, and hence,
$a^4$
invertible implies a is invertible, and hence,
![]() $a^4$
is not a minimal invertible piece). Also, in this example, the subgroup generated by the pieces
$a^4$
is not a minimal invertible piece). Also, in this example, the subgroup generated by the pieces
![]() $X = \{ ab^{-1}a^2, b, a^{4} \}$
is in fact a one-relator group since (as explained before the statement of the theorem), but this theorem shows that it does not admit the ‘obvious’ one-relator presentation given by replacing the pieces by letters in the obvious way.
$X = \{ ab^{-1}a^2, b, a^{4} \}$
is in fact a one-relator group since (as explained before the statement of the theorem), but this theorem shows that it does not admit the ‘obvious’ one-relator presentation given by replacing the pieces by letters in the obvious way.
However, this example is the first evidence that there may exist examples of one-relator special inverse monoids with group of units not being a one-relator group. This will be explored further in the next section.
6 A construction
In this section, we shall give a general construction, which will then be used in the next section to give examples of special inverse monoids that exhibit unexpected behaviour in terms of their groups of units.
The construction we give here was used in [Reference Gray6] to give an example of a one-relator special inverse monoid with undecidable word problem. It has also been used in the papers [Reference Gray and Dolinka7] and [Reference Gray, Silva and Szakacs9] to construct counterexamples to questions about the prefix membership problem for one-relator groups, and the word problem for finitely presented inverse monoids with hyperbolic Schützenberger graphs. To make this paper self-contained, we provide full details of the construction here. Also, we use slightly different notational conventions than those used in [Reference Gray6]. Some of the results we need about this construction have already been proved in [Reference Gray6], but there are some other facts about the construction that we need here that are not proved in that paper, so we will provide the necessary proofs.
6.1 The construction
Let
![]() $A=\{a_1,\dots ,a_n\}$
be a finite nonempty alphabet. Let
$A=\{a_1,\dots ,a_n\}$
be a finite nonempty alphabet. Let
![]() $Q = \{ r_i \::\: i \in I \}$
be a subset of
$Q = \{ r_i \::\: i \in I \}$
be a subset of
![]() $\overline {A}^{*}$
, where I is nonempty, and we assume there is a distinguished symbol
$\overline {A}^{*}$
, where I is nonempty, and we assume there is a distinguished symbol
![]() $1 \in I$
. Let
$1 \in I$
. Let
![]() $W = \{ w_j \::\: j=1,\dots , k \}$
be a finite subset of
$W = \{ w_j \::\: j=1,\dots , k \}$
be a finite subset of
![]() $\overline {A}^{*}$
. Let t be a symbol not in A.
$\overline {A}^{*}$
. Let t be a symbol not in A.
We define two groups which depend on Q by
Given a list of words
![]() $u_1, \ldots , u_m \in \overline {A}^{*}$
, we define
$u_1, \ldots , u_m \in \overline {A}^{*}$
, we define
noting that this clearly freely reduces to
![]() $1$
in the free group
$1$
in the free group
![]() $F_A$
.
$F_A$
.
We also define two inverse monoids, the first depending on Q, and the second on both Q and W, as follows:
where
We make the following observations about the groups and monoids we have just defined:
-
(M1)
 $K_Q$
is the maximal group image of
$K_Q$
is the maximal group image of
 $N_Q$
, and
$N_Q$
, and
 $G_Q$
is the maximal group image of
$G_Q$
is the maximal group image of
 $M_{Q,W}$
(under the natural homomorphisms).
$M_{Q,W}$
(under the natural homomorphisms). -
(M2) Presentation (28) for
 $M_{Q,W}$
is equivalent to (30)in the sense that two words over
$M_{Q,W}$
is equivalent to (30)in the sense that two words over $$ \begin{align} M_{Q,W}= \operatorname{Inv}\bigl\langle &{A, t}\:|\: r_i=1, \ a_j a_j^{-1} = a_j^{-1} a_j = 1,\\& t w_l t^{-1} t w_l^{-1} t^{-1}= 1 \ (i{\in} I,\ j \in [n],\ l{\in} [k]) \bigr\rangle \nonumber\end{align} $$
$$ \begin{align} M_{Q,W}= \operatorname{Inv}\bigl\langle &{A, t}\:|\: r_i=1, \ a_j a_j^{-1} = a_j^{-1} a_j = 1,\\& t w_l t^{-1} t w_l^{-1} t^{-1}= 1 \ (i{\in} I,\ j \in [n],\ l{\in} [k]) \bigr\rangle \nonumber\end{align} $$
 $\overline {(A \cup \{t\})}$
are equal modulo the relations of (28) if and only if they are equal modulo the relations (30).
$\overline {(A \cup \{t\})}$
are equal modulo the relations of (28) if and only if they are equal modulo the relations (30).
-
(M3) All the generators
 $a_j \in A$
are invertible in
$a_j \in A$
are invertible in
 $M_{Q,W}$
, while t and all of the elements
$M_{Q,W}$
, while t and all of the elements
 $t w_l t^{-1}$
are right invertible in M.
$t w_l t^{-1}$
are right invertible in M. -
(M4)
 $M_{Q,W}$
maps naturally onto the bicyclic monoid
$M_{Q,W}$
maps naturally onto the bicyclic monoid
 $B={\operatorname {Inv}\bigl \langle {b}\:|\:{bb^{-1}=1} \bigr \rangle }$
via
$B={\operatorname {Inv}\bigl \langle {b}\:|\:{bb^{-1}=1} \bigr \rangle }$
via
 $a_j\mapsto 1$
,
$a_j\mapsto 1$
,
 $t\mapsto b$
.
$t\mapsto b$
. -
(M5) t is not invertible in
 $M_{Q,W}$
.
$M_{Q,W}$
.
Indeed, observation (M1) is immediate from the definitions and the general fact that the maximal group image of an inverse monoid defined by a presentation is the group defined by the same presentation. (M2) can be proved using Lemma 2.2. A full proof is given in [Reference Gray6, Lemma 3.3]. (M3) follows from (M2) and the defining relations in the presentation (30). (M4) is immediate from the fact that
![]() $M_{Q,W}$
is given by the presentation (30) and then the observation that replacing a by
$M_{Q,W}$
is given by the presentation (30) and then the observation that replacing a by
![]() $1$
and t by b in that presentation just leaves the relation
$1$
and t by b in that presentation just leaves the relation
![]() $bb^{-1}bb^{-1}=1$
which certainly holds in B. (M5) follows from (M4) since b is not invertible in the bicyclic monoid B, and the image of an invertible element of a monoid under a surjective homomorphism must again be an invertible element.
$bb^{-1}bb^{-1}=1$
which certainly holds in B. (M5) follows from (M4) since b is not invertible in the bicyclic monoid B, and the image of an invertible element of a monoid under a surjective homomorphism must again be an invertible element.
We will make use of the following general lemma, which follows immediately from the universal properties of free products.
Lemma 6.1. Let G and H be groups. Let M be a submonoid of G and N be a submonoid of H. Then the submonoid of the free product
![]() $G \ast H$
generated by
$G \ast H$
generated by
![]() $M \cup N$
is isomorphic to
$M \cup N$
is isomorphic to
![]() $M \ast N$
.
$M \ast N$
.
The following lemma is probably well known, but we give a proof for completeness.
Lemma 6.2. Let H be a group. Then the subgroup of the free product
![]() $G = H \ast F_t$
generated by
$G = H \ast F_t$
generated by
![]() $H \cup tHt^{-1}$
is isomorphic to
$H \cup tHt^{-1}$
is isomorphic to
![]() $H \ast H$
.
$H \ast H$
.
Proof. Set
![]() $\overline {H} = t H t^{-1} \leq G = H * F_t$
. Let L be the subgroup of G generated by
$\overline {H} = t H t^{-1} \leq G = H * F_t$
. Let L be the subgroup of G generated by
![]() $H \cup \overline {H}$
. Now H and
$H \cup \overline {H}$
. Now H and
![]() $\overline {H}$
are subgroups of L and
$\overline {H}$
are subgroups of L and
![]() $H \cap \overline {H} = \varnothing $
by the normal form theorem for elements in free products of groups. Given a reduced sequence
$H \cap \overline {H} = \varnothing $
by the normal form theorem for elements in free products of groups. Given a reduced sequence
![]() $g_1, g_2, \ldots , g_n$
, where the
$g_1, g_2, \ldots , g_n$
, where the
![]() $g_i$
all belong to L and alternate between H and
$g_i$
all belong to L and alternate between H and
![]() $\overline {H}$
, if
$\overline {H}$
, if
![]() $n> 0$
, then it again follows from the normal form theorem in G that
$n> 0$
, then it again follows from the normal form theorem in G that
![]() $g_1 g_2 \ldots g_n \neq 1$
. Thus, all the conditions of [Reference Lyndon and Schupp18, Lemma 1.7] are satisfied, and we conclude that
$g_1 g_2 \ldots g_n \neq 1$
. Thus, all the conditions of [Reference Lyndon and Schupp18, Lemma 1.7] are satisfied, and we conclude that
![]() $L \cong H * \overline {H}$
. Clearly,
$L \cong H * \overline {H}$
. Clearly,
![]() $H \cong \overline {H}$
since they are conjugate subgroups of G. This completes the proof that
$H \cong \overline {H}$
since they are conjugate subgroups of G. This completes the proof that
![]() $L \cong H * H$
.
$L \cong H * H$
.
We are now in a position to state and prove the main result of this section, which establishes the key properties of the monoid
![]() $M_{Q,W}$
that we will need in our applications and examples in the next section.
$M_{Q,W}$
that we will need in our applications and examples in the next section.
Theorem 6.3. With the above definitions and notation, the special inverse monoid
![]() $M_{Q,W}$
has the following properties.
$M_{Q,W}$
has the following properties.
-
(i) The presentation (28) of
 $M_{Q,W}$
has the same number of defining relations as the original presentation (25) of
$M_{Q,W}$
has the same number of defining relations as the original presentation (25) of
 $K_Q$
.
$K_Q$
. -
(ii) The monoid
 $M_{Q,W}$
is E-unitary.
$M_{Q,W}$
is E-unitary. -
(iii) Let
 $T_W$
be the submonoid of the group
$T_W$
be the submonoid of the group
 $K_Q$
generated by W. Then the submonoid of right units
$K_Q$
generated by W. Then the submonoid of right units
 $R(M_{Q,W})$
of
$R(M_{Q,W})$
of
 $M_{Q,W}$
is isomorphic to the submonoid of the group
$M_{Q,W}$
is isomorphic to the submonoid of the group
 $G_Q=K_Q \ast F_t$
generated by
$G_Q=K_Q \ast F_t$
generated by
 $\{ t\} \cup K_Q \cup t T_W t^{-1}$
.
$\{ t\} \cup K_Q \cup t T_W t^{-1}$
. -
(iv) Let
 $V_{Q,W}$
be the submonoid of
$V_{Q,W}$
be the submonoid of
 $R(M_{Q,W})$
generated by
$R(M_{Q,W})$
generated by
 $A \cup A^{-1} \cup tWt^{-1}$
. Then
$A \cup A^{-1} \cup tWt^{-1}$
. Then
 $V_{Q,M}$
is isomorphic to the free product
$V_{Q,M}$
is isomorphic to the free product
 $K_Q \ast T_W$
and the complement of
$K_Q \ast T_W$
and the complement of
 $V_{Q,W}$
in
$V_{Q,W}$
in
 $R(M_{Q,W})$
is an ideal of
$R(M_{Q,W})$
is an ideal of
 $R(M_{Q,W})$
.
$R(M_{Q,W})$
. -
(v) The group of units
 $U(M_{Q,W})$
of
$U(M_{Q,W})$
of
 $M_{Q,W}$
is isomorphic to the free product
$M_{Q,W}$
is isomorphic to the free product
 $ K_Q \ast H_{W'}, $
where
$ K_Q \ast H_{W'}, $
where
 $H_{W'}$
is the subgroup of
$H_{W'}$
is the subgroup of
 $K_Q$
generated by the subset
$K_Q$
generated by the subset
 $W'$
of W defined by In particular, if
$W'$
of W defined by In particular, if $$\begin{align*}W' = \{ w_l \in W: tw_lt^{-1} \ \mbox{is invertible in} \; M_{Q,W} \}. \end{align*}$$
$$\begin{align*}W' = \{ w_l \in W: tw_lt^{-1} \ \mbox{is invertible in} \; M_{Q,W} \}. \end{align*}$$
 $W = W^{-1}$
, then
$W = W^{-1}$
, then
 $W'=W$
, and so
$W'=W$
, and so
 $U(M_{Q,W}) \cong K_Q \ast H_W$
.
$U(M_{Q,W}) \cong K_Q \ast H_W$
.
-
(vi) If
 $R(M_{Q,W})$
is finitely presented, then
$R(M_{Q,W})$
is finitely presented, then
 $K_Q$
and
$K_Q$
and
 $T_W$
are both finitely presented.
$T_W$
are both finitely presented.
Proof. (i) is obvious since they both have
![]() $|I|$
defining relations, and (ii) is [Reference Gray6, Theorem 3.8].
$|I|$
defining relations, and (ii) is [Reference Gray6, Theorem 3.8].
(iii) By [Reference Margolis and Meakin21, Lemma 1.5], since
![]() $M_{Q,W}$
is E-unitary, it follows that the canonical homomorphism
$M_{Q,W}$
is E-unitary, it follows that the canonical homomorphism
![]() $\theta : M_{Q,W} \rightarrow G_Q=K_Q\ast F_t$
from
$\theta : M_{Q,W} \rightarrow G_Q=K_Q\ast F_t$
from
![]() $M_{Q,W}$
onto its maximal group image (see (M1)) induces an embedding of each
$M_{Q,W}$
onto its maximal group image (see (M1)) induces an embedding of each
![]() $\mathscr {R}$
-class of M into
$\mathscr {R}$
-class of M into
![]() $G_Q$
. In particular,
$G_Q$
. In particular,
![]() $\theta $
induces an embedding of the right units
$\theta $
induces an embedding of the right units
![]() $R(M_{Q,W})$
into
$R(M_{Q,W})$
into
![]() $G_Q$
. By the argument given in the proof of [Reference Ivanov, Margolis and Meakin12, Proposition 4.2], it follows that
$G_Q$
. By the argument given in the proof of [Reference Ivanov, Margolis and Meakin12, Proposition 4.2], it follows that
![]() $R(M_{Q,W})$
is generated by the prefixes of the defining relators in the presentation (30) of
$R(M_{Q,W})$
is generated by the prefixes of the defining relators in the presentation (30) of
![]() $M_{Q,W}$
. Note that in [Reference Ivanov, Margolis and Meakin12, Proposition 4.2], an assumption is made that the defining relators are all cyclically reduced words, but this hypothesis is not used in the proof, and so the statement holds with that assumption removed (cf. Theorem 1.3).
$M_{Q,W}$
. Note that in [Reference Ivanov, Margolis and Meakin12, Proposition 4.2], an assumption is made that the defining relators are all cyclically reduced words, but this hypothesis is not used in the proof, and so the statement holds with that assumption removed (cf. Theorem 1.3).
This implies that
![]() $R(M_{Q,W})$
is isomorphic to the submonoid of
$R(M_{Q,W})$
is isomorphic to the submonoid of
![]() $G_Q$
generated by the prefixes of the defining relators in the presentation (30). We claim that this is equal to the submonoid of
$G_Q$
generated by the prefixes of the defining relators in the presentation (30). We claim that this is equal to the submonoid of
![]() $G_Q$
generated by the set
$G_Q$
generated by the set
Indeed, we have already observed that all these words represent right invertible elements (see (M3)). Furthermore, all the prefixes of relators in (30) are equal in
![]() $M_{Q,W}$
to products of those words. This is immediate for the prefixes of
$M_{Q,W}$
to products of those words. This is immediate for the prefixes of
![]() $r_i$
,
$r_i$
,
![]() $a_ja_j^{-1}$
,
$a_ja_j^{-1}$
,
![]() $a_j^{-1}a_j$
, as they are products of generators from A. The proper prefixes of
$a_j^{-1}a_j$
, as they are products of generators from A. The proper prefixes of
![]() $tw_lt^{-1}$
are products of generators from
$tw_lt^{-1}$
are products of generators from
![]() $A\cup \{t\}$
. Finally, longer prefixes of
$A\cup \{t\}$
. Finally, longer prefixes of
![]() $tw_lt^{-1}tw_l^{-1}t^{-1}$
are equal in
$tw_lt^{-1}tw_l^{-1}t^{-1}$
are equal in
![]() $M_{Q,W}$
to prefixes of
$M_{Q,W}$
to prefixes of
![]() $tw_lt^{-1}$
by Lemma 2.2(i). This completes the proof of the claim that
$tw_lt^{-1}$
by Lemma 2.2(i). This completes the proof of the claim that
![]() $R(M_{Q,W})$
is isomorphic to the submonoid of
$R(M_{Q,W})$
is isomorphic to the submonoid of
![]() $G_Q$
generated by Y.
$G_Q$
generated by Y.
Since the submonoid of
![]() $G_Q$
generated by
$G_Q$
generated by
![]() $A \cup A^{-1}$
is
$A \cup A^{-1}$
is
![]() $K_Q$
, and the submonoid of
$K_Q$
, and the submonoid of
![]() $G_Q$
generated by
$G_Q$
generated by
![]() $\{ tw_j t^{-1}: j \in [k] \}$
is
$\{ tw_j t^{-1}: j \in [k] \}$
is
![]() $t T_W t^{-1}$
, this completes the proof of (iii).
$t T_W t^{-1}$
, this completes the proof of (iii).
(iv) As in the previous part, E-unitarity of
![]() $M_{Q,W}$
implies that
$M_{Q,W}$
implies that
![]() $V_{Q,W}$
is isomorphic to the submonoid of
$V_{Q,W}$
is isomorphic to the submonoid of
![]() $G_Q$
generated by
$G_Q$
generated by
![]() $K_Q \cup t T_W t^{-1}$
. By Lemma 6.2, the submonoid of
$K_Q \cup t T_W t^{-1}$
. By Lemma 6.2, the submonoid of
![]() $K_Q \ast F_t$
generated by
$K_Q \ast F_t$
generated by
![]() $K_Q \cup t K_Q t^{-1}$
is isomorphic to
$K_Q \cup t K_Q t^{-1}$
is isomorphic to
![]() $K_Q \ast K_Q$
. Combining this fact with Lemma 6.1, we conclude that the submonoid of
$K_Q \ast K_Q$
. Combining this fact with Lemma 6.1, we conclude that the submonoid of
![]() $K_Q \ast F_t$
generated by
$K_Q \ast F_t$
generated by
![]() $K_Q \cup t T_W t^{-1}$
is isomorphic to
$K_Q \cup t T_W t^{-1}$
is isomorphic to
![]() $K_Q \ast T_W$
. Hence, we have shown that
$K_Q \ast T_W$
. Hence, we have shown that
![]() $V_{Q,W}$
is isomorphic to
$V_{Q,W}$
is isomorphic to
![]() $K_Q \ast T_W$
.
$K_Q \ast T_W$
.
To see that
![]() $R(M_{Q,W}) \setminus V_{Q,W}$
is an ideal in
$R(M_{Q,W}) \setminus V_{Q,W}$
is an ideal in
![]() $R(M_{Q,W})$
, it suffices to observe that under the natural epimorphism from
$R(M_{Q,W})$
, it suffices to observe that under the natural epimorphism from
![]() $M_{Q,W}$
onto the bicyclic monoid B (see (M4)), the submonoid
$M_{Q,W}$
onto the bicyclic monoid B (see (M4)), the submonoid
![]() $R(M_{Q,W})$
is mapped onto
$R(M_{Q,W})$
is mapped onto
![]() $R'=\{ b^i\::\: i\in {\mathbb {N}}_0\}$
, while
$R'=\{ b^i\::\: i\in {\mathbb {N}}_0\}$
, while
![]() $R(M_{Q,W}) \setminus V_{Q,W}$
is mapped onto
$R(M_{Q,W}) \setminus V_{Q,W}$
is mapped onto
![]() $V'=\{ b^i\::\: i\in {\mathbb {N}}\}$
, and that
$V'=\{ b^i\::\: i\in {\mathbb {N}}\}$
, and that
![]() $V'$
is an ideal of
$V'$
is an ideal of
![]() $R'$
. Since the preimage of an ideal, with respect to a surjective homomorphism, is itself an ideal, this completes the proof that the complement of
$R'$
. Since the preimage of an ideal, with respect to a surjective homomorphism, is itself an ideal, this completes the proof that the complement of
![]() $V_{Q,W}$
in
$V_{Q,W}$
in
![]() $R(M_{Q,W})$
is an ideal of
$R(M_{Q,W})$
is an ideal of
![]() $R(M_{Q,W})$
.
$R(M_{Q,W})$
.
(v) Observe that
![]() $U(M_{Q,W})$
is contained in
$U(M_{Q,W})$
is contained in
![]() $R(M_{Q,W})$
and the complement
$R(M_{Q,W})$
and the complement
![]() $R(M_{Q,W}) \setminus U(M_{Q,W})$
is an ideal of the monoid
$R(M_{Q,W}) \setminus U(M_{Q,W})$
is an ideal of the monoid
![]() $R(M_{Q,W})$
. Also, it follows from the proof of part (iii) that
$R(M_{Q,W})$
. Also, it follows from the proof of part (iii) that
![]() $R(M_{Q,W})$
is the submonoid of
$R(M_{Q,W})$
is the submonoid of
![]() $M_{Q,W}$
generated by
$M_{Q,W}$
generated by
![]() $\{t\} \cup A \cup A^{-1} \cup tWt^{-1}$
. Since
$\{t\} \cup A \cup A^{-1} \cup tWt^{-1}$
. Since
![]() $R(M_{Q,W}) \setminus U(M_{Q,W})$
is an ideal of the monoid
$R(M_{Q,W}) \setminus U(M_{Q,W})$
is an ideal of the monoid
![]() $R(M_{Q,W})$
, it follows that
$R(M_{Q,W})$
, it follows that
is a monoid generating set for
![]() $U(M_{Q,W})$
(this follows from the more general fact [Reference Gray6, Lemma 3.5]). By (M5), t is not invertible in
$U(M_{Q,W})$
(this follows from the more general fact [Reference Gray6, Lemma 3.5]). By (M5), t is not invertible in
![]() $M_{Q,W}$
and hence
$M_{Q,W}$
and hence
![]() $t \not \in Z$
. By (M3),
$t \not \in Z$
. By (M3),
![]() $A \cup A^{-1} \subseteq Z$
. The remaining elements of Z are those from the set
$A \cup A^{-1} \subseteq Z$
. The remaining elements of Z are those from the set
![]() $tWt^{-1} \cap U(M_{Q,W})$
which is by definition equal to the set
$tWt^{-1} \cap U(M_{Q,W})$
which is by definition equal to the set
![]() $tW't^{-1}$
, where
$tW't^{-1}$
, where
This proves that the group of units
![]() $U(M_{Q,W})$
is isomorphic to the submonoid of
$U(M_{Q,W})$
is isomorphic to the submonoid of
![]() $R(M_{Q,W})$
generated by
$R(M_{Q,W})$
generated by
It follows that the image of
![]() $U(M_{Q,W})$
under the isomorphism from (iii) is the submonoid of
$U(M_{Q,W})$
under the isomorphism from (iii) is the submonoid of
![]() $G_Q = K_Q\ast F_t$
generated by the image of Z under the isomorphism from (iii). Since the submonoid of
$G_Q = K_Q\ast F_t$
generated by the image of Z under the isomorphism from (iii). Since the submonoid of
![]() $K_Q\ast F_t$
generated by
$K_Q\ast F_t$
generated by
![]() $A \cup A^{-1}$
is
$A \cup A^{-1}$
is
![]() $K_Q$
, it follows that the image of
$K_Q$
, it follows that the image of
![]() $U(M_{Q,W})$
under the isomorphism from (iii) is precisely the submonoid of
$U(M_{Q,W})$
under the isomorphism from (iii) is precisely the submonoid of
![]() $K_Q \ast F_t$
generated by
$K_Q \ast F_t$
generated by
![]() $K_Q\cup tW't^{-1}$
. Since
$K_Q\cup tW't^{-1}$
. Since
![]() $U(M_{Q,W})$
is a group, this must also be equal to the subgroup of
$U(M_{Q,W})$
is a group, this must also be equal to the subgroup of
![]() $K_Q \ast F_t$
generated by
$K_Q \ast F_t$
generated by
![]() $K_Q\cup tW't^{-1}$
. Under the isomorphism from (iv), this corresponds to
$K_Q\cup tW't^{-1}$
. Under the isomorphism from (iv), this corresponds to
![]() $K_Q\ast H_{W'}$
, proving the first assertion. For the second assertion, observe that if
$K_Q\ast H_{W'}$
, proving the first assertion. For the second assertion, observe that if
![]() $W=W^{-1}$
then
$W=W^{-1}$
then
![]() $W'=W$
immediately from the presentation (30) for
$W'=W$
immediately from the presentation (30) for
![]() $M_{Q,W}$
.
$M_{Q,W}$
.
(vi) If
![]() $R(M_{Q,W})$
is finitely presented, then by part (iv), it follows that
$R(M_{Q,W})$
is finitely presented, then by part (iv), it follows that
![]() $V_{Q,W}$
is finitely presented since its complement is an ideal. The fact that finite presentability is inherited by submonoids with ideal complement is well-known, for example, it is a corollary of [Reference Gray and Ruškuc8, Theorem B]. Therefore,
$V_{Q,W}$
is finitely presented since its complement is an ideal. The fact that finite presentability is inherited by submonoids with ideal complement is well-known, for example, it is a corollary of [Reference Gray and Ruškuc8, Theorem B]. Therefore,
![]() $K_Q \ast T_W$
is finitely presented, which implies that
$K_Q \ast T_W$
is finitely presented, which implies that
![]() $K_Q$
and
$K_Q$
and
![]() $T_W$
are both finitely presented, being retracts of
$T_W$
are both finitely presented, being retracts of
![]() $K_Q \ast T_W$
. Here, we have used the fact that any retract of a finitely presented monoid is again finitely presented. This follows from the proof of [Reference Wang and Pride26, Theorem 3.4] (see, in particular, the remark in [Reference Wang and Pride26] immediately after the proof of Theorem 3.4 of that paper).
$K_Q \ast T_W$
. Here, we have used the fact that any retract of a finitely presented monoid is again finitely presented. This follows from the proof of [Reference Wang and Pride26, Theorem 3.4] (see, in particular, the remark in [Reference Wang and Pride26] immediately after the proof of Theorem 3.4 of that paper).
7 Applications to further examples
The central theme in this article as outlined in Section 1 has been to investigate the extent to which analogues of the results of Adjan/Makanin/Zhang for finitely presented special monoids can be proved for special inverse monoid presentations. Both the example at the start of Section 3 and the O’Hare monoid example considered in Section 5.1 show that while the obvious naïve generalisation to special inverse monoids does not hold, by an appropriate choice of basis, the hypotheses of Theorem 3.1 are satisfied by these two examples. In particular, in each case, their groups of units are one-relator groups. As explained in Section 1, it is natural to ask whether the assumptions of Theorem 3.1 are perhaps always satisfied, or at least always in the case of one-relator presentations. The main results in Section 3 identify several sufficient conditions under which the assumptions of Theorem 3.1 are satisfied (see, for example, the conditions (F1), (F2), and (F3)).
In this section, we will use the general construction and Theorem 6.3 from the previous section to prove that in general, none of the main results of Adjan/Makanin/Zhang for special monoids can be extended to special inverse monoids.
We also prove a result which shows a close relationship between finite presentability of the units of special one-relator inverse monoids and the question of coherence of one-relator groups.
7.1 A one-relator special inverse monoid whose group of units is not one-relator
If we input a one-relator group
![]() $K_Q$
into the construction from Section 6, then Theorem 6.3(v) shows that the group of units of the one-relator special inverse monoid
$K_Q$
into the construction from Section 6, then Theorem 6.3(v) shows that the group of units of the one-relator special inverse monoid
![]() $M_{Q,W}$
is isomorphic to the free product of groups
$M_{Q,W}$
is isomorphic to the free product of groups
![]() $K_Q \ast H_{W}$
, where by appropriate choice of W in the construction, the group
$K_Q \ast H_{W}$
, where by appropriate choice of W in the construction, the group
![]() $H_W^{\prime }$
can be any finitely generated subgroup of
$H_W^{\prime }$
can be any finitely generated subgroup of
![]() $K_Q$
that we please. In particular, the set W can be chosen so that the group of units of the one-relator special inverse monoid
$K_Q$
that we please. In particular, the set W can be chosen so that the group of units of the one-relator special inverse monoid
![]() $M_{Q,W}$
is isomorphic to
$M_{Q,W}$
is isomorphic to
![]() $K_Q \ast K_Q$
.
$K_Q \ast K_Q$
.
Since in general, the free product
![]() $K_Q \ast K_Q$
of a one-relator group
$K_Q \ast K_Q$
of a one-relator group
![]() $K_Q$
with itself is not a one-relator group, this can be used to construct examples of special one-relator inverse monoids whose groups of units are not one-relator. This leads to the following result.
$K_Q$
with itself is not a one-relator group, this can be used to construct examples of special one-relator inverse monoids whose groups of units are not one-relator. This leads to the following result.
Theorem 7.1. There exists a one-relator special inverse monoid
![]() $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{w=1} \bigr \rangle }$
, whose group of units G is not a one-relator group with respect to any finite generating set. Moreover, M can be chosen to be E-unitary.
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{w=1} \bigr \rangle }$
, whose group of units G is not a one-relator group with respect to any finite generating set. Moreover, M can be chosen to be E-unitary.
Proof. Let
![]() $A = \{a,b,c,d\}$
, let
$A = \{a,b,c,d\}$
, let
![]() $Q = \{ aba^{-1}b^{-1}cdc^{-1}d^{-1} \}$
and set
$Q = \{ aba^{-1}b^{-1}cdc^{-1}d^{-1} \}$
and set
![]() $W = \{a^{\pm 1},b^{\pm 1},c^{\pm 1},d^{\pm 1}\}$
. Then, by Theorem 6.3 (i), (ii), (v), the monoid
$W = \{a^{\pm 1},b^{\pm 1},c^{\pm 1},d^{\pm 1}\}$
. Then, by Theorem 6.3 (i), (ii), (v), the monoid
![]() $M=M_{Q,W}$
is a one-relator E-unitary special inverse monoid with group of units
$M=M_{Q,W}$
is a one-relator E-unitary special inverse monoid with group of units
![]() $U(M) \cong K \ast K$
, where
$U(M) \cong K \ast K$
, where
Note that K is a torsion-free one-relator group. In fact, it is a one-relator surface group: the fundamental group of a surface of genus
![]() $2$
. To complete the proof, it now suffices to prove that the free product
$2$
. To complete the proof, it now suffices to prove that the free product
![]() $K \ast K$
of this one-relator group with itself is not a one-relator group with respect to any finite generating set. One way to see this is as follows.
$K \ast K$
of this one-relator group with itself is not a one-relator group with respect to any finite generating set. One way to see this is as follows.
It follows from Lyndon’s Identity theorem [Reference Lyndon17], see also [Reference Brown4, page 37, Example 3], that
![]() $H_2 (K) = \mathbb {Z}$
, where
$H_2 (K) = \mathbb {Z}$
, where
![]() $H_2(K)$
denotes the second homology group of K. Indeed, it follows from Lyndon’s results that if
$H_2(K)$
denotes the second homology group of K. Indeed, it follows from Lyndon’s results that if
![]() $G = {\operatorname {Gp}\bigl \langle {X}\:|\:{s=1} \bigr \rangle }$
is a torsion-free one-relator group, where s is a cyclically reduced word, then
$G = {\operatorname {Gp}\bigl \langle {X}\:|\:{s=1} \bigr \rangle }$
is a torsion-free one-relator group, where s is a cyclically reduced word, then
 $$\begin{align*}H_2(G) \cong \begin{cases} \mathbb{Z} & \mbox{if } s \in F_X^{\prime} \\ 0 & \mbox{otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}H_2(G) \cong \begin{cases} \mathbb{Z} & \mbox{if } s \in F_X^{\prime} \\ 0 & \mbox{otherwise,} \end{cases} \end{align*}$$
where
![]() $F_X^{\prime }$
is the derived subgroup of the free group. From
$F_X^{\prime }$
is the derived subgroup of the free group. From
![]() $H_2(K) = \mathbb {Z}$
it follows by [Reference Weibel27, Corollary 6.2.10] or [Reference Hilton and Stammbach11, page 220, Theorem 14.2] that
$H_2(K) = \mathbb {Z}$
it follows by [Reference Weibel27, Corollary 6.2.10] or [Reference Hilton and Stammbach11, page 220, Theorem 14.2] that
Clearly,
![]() $K \ast K$
is torsion free, since K is torsion free, and thus by Lyndon’s result above, it follows that
$K \ast K$
is torsion free, since K is torsion free, and thus by Lyndon’s result above, it follows that
![]() $K \ast K$
cannot be a one-relator group with respect to any generating set.
$K \ast K$
cannot be a one-relator group with respect to any generating set.
7.2 A one-relator special inverse monoid whose group of units is finitely presented, but the monoid of right units is not finitely presented
An important structural result arising from the work of Adjan/Makanin/Zhang is that the monoid of right units of a finitely presented special monoid is isomorphic to a free product of its group of units and a finitely generated free monoid. The results in this subsection will show that this is far from being true in the case of special inverse monoids.
Theorem 6.3(vi) tells us that, for that construction, finite presentability of the right units
![]() $R(M_{Q,W})$
of the special inverse monoid
$R(M_{Q,W})$
of the special inverse monoid
![]() $M_{Q,W}$
is determined by finite presentability of the group
$M_{Q,W}$
is determined by finite presentability of the group
![]() $K_Q$
, and of the submonoid
$K_Q$
, and of the submonoid
![]() $T_W$
of
$T_W$
of
![]() $K_Q$
. Since there are examples of finitely generated submonoids of one-relator groups that are not finitely presented, this leads to the following result.
$K_Q$
. Since there are examples of finitely generated submonoids of one-relator groups that are not finitely presented, this leads to the following result.
Theorem 7.2. There exists a one-relator special inverse monoid
![]() $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
with the following properties:
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
with the following properties:
-
• the group of units G of M is finitely presented, and
-
• the submonoid of right units R of M is finitely generated but not finitely presented.
Hence, there is no finitely presented monoid N, such that
![]() $R \cong G \ast N$
. In particular, there is no free monoid F, such that
$R \cong G \ast N$
. In particular, there is no free monoid F, such that
![]() $R \cong G \ast F$
. Throughout, M can be chosen to be E-unitary.
$R \cong G \ast F$
. Throughout, M can be chosen to be E-unitary.
Proof. Let
![]() $A = \{a_1, \ldots , a_n\}$
, let
$A = \{a_1, \ldots , a_n\}$
, let
![]() $Q= \varnothing $
and let
$Q= \varnothing $
and let
![]() $W = \{w_1, \ldots , w_k\}$
be a finite subset of
$W = \{w_1, \ldots , w_k\}$
be a finite subset of
![]() $A^{*}$
, such that the submonoid of
$A^{*}$
, such that the submonoid of
![]() $A^{*}$
generated by W is not finitely presented (e.g. [Reference Campbell, Robertson, Ruškuc and Thomas5, Example 4.5]). Then we have
$A^{*}$
generated by W is not finitely presented (e.g. [Reference Campbell, Robertson, Ruškuc and Thomas5, Example 4.5]). Then we have
The maximal group image of
![]() $M_{Q,W}$
is the free group
$M_{Q,W}$
is the free group
![]() $G_Q=F_{A \cup \{ t \}}$
, and
$G_Q=F_{A \cup \{ t \}}$
, and
![]() $K_Q = F_A$
. The submonoid
$K_Q = F_A$
. The submonoid
![]() $T_W$
of
$T_W$
of
![]() $K_Q$
generated by W is not finitely presented by choice of W, and hence by Theorem 6.3(vi), the submonoid of right units
$K_Q$
generated by W is not finitely presented by choice of W, and hence by Theorem 6.3(vi), the submonoid of right units
![]() $R(M_{Q,W})$
is not finitely presented. The submonoid of right units
$R(M_{Q,W})$
is not finitely presented. The submonoid of right units
![]() $R(M_{Q,W})$
is finitely generated by Theorem 6.3(iii). Since
$R(M_{Q,W})$
is finitely generated by Theorem 6.3(iii). Since
![]() $M_{Q,W}$
is E-unitary and the maximal group image is free, it follows that the group of units of
$M_{Q,W}$
is E-unitary and the maximal group image is free, it follows that the group of units of
![]() $M_{Q,W}$
is a finitely generated free group and, in particular, is finitely presented. Since the group of units G is finitely presented, it follows that for any finitely presented monoid N, the free product
$M_{Q,W}$
is a finitely generated free group and, in particular, is finitely presented. Since the group of units G is finitely presented, it follows that for any finitely presented monoid N, the free product
![]() $G \ast N$
is also finitely presented. As R is not finitely presented, we conclude that there is no finitely presented monoid N, such that
$G \ast N$
is also finitely presented. As R is not finitely presented, we conclude that there is no finitely presented monoid N, such that
![]() $R \cong G \ast N$
. For the last statement, if
$R \cong G \ast N$
. For the last statement, if
![]() $R \cong G \ast F$
, then since R is finitely generated, it would follow that F is finitely generated, and hence finitely presented (since F is free). But since G is finitely presented, this contradicts the fact that
$R \cong G \ast F$
, then since R is finitely generated, it would follow that F is finitely generated, and hence finitely presented (since F is free). But since G is finitely presented, this contradicts the fact that
![]() $R \cong G \ast F$
is not finitely presented.
$R \cong G \ast F$
is not finitely presented.
Remark 7.3. If we modify the above construction slightly and instead simply take the inverse monoid
then again the right units will not be finitely presented, but the group of units in this case will be the trivial group. To prove the latter statement, it is sufficient to observe that the elements
![]() $tw_lt^{-1}$
(with
$tw_lt^{-1}$
(with
![]() $w_l$
nonempty) are not invertible in the submonoid
$w_l$
nonempty) are not invertible in the submonoid
![]() $tT_Wt^{-1}$
of
$tT_Wt^{-1}$
of
![]() $G_{Q,W}=F_{A \cup \{ t \}}$
. To see this, note that in the proof of Theorem 7.2, we took
$G_{Q,W}=F_{A \cup \{ t \}}$
. To see this, note that in the proof of Theorem 7.2, we took
![]() ${W = \{w_1, \ldots , w_k\}}$
be a certain finite subset of the free monoid
${W = \{w_1, \ldots , w_k\}}$
be a certain finite subset of the free monoid
![]() $A^{*}$
. Hence, the submonoid
$A^{*}$
. Hence, the submonoid
![]() $T_W$
of
$T_W$
of
![]() $K_Q = F_A$
generated by W must also be contained in
$K_Q = F_A$
generated by W must also be contained in
![]() $A^{*}$
, and hence must have a trivial group of units, since
$A^{*}$
, and hence must have a trivial group of units, since
![]() $T_W \subseteq A^{*} \subseteq F_A$
and
$T_W \subseteq A^{*} \subseteq F_A$
and
![]() $A^{*}$
has a trivial group of units. Since the submonoid
$A^{*}$
has a trivial group of units. Since the submonoid
![]() $tT_Wt^{-1}$
of
$tT_Wt^{-1}$
of
![]() $G_{Q,W}=F_{A \cup \{ t \}}$
is isomorphic to the monoid
$G_{Q,W}=F_{A \cup \{ t \}}$
is isomorphic to the monoid
![]() $T_W$
, it follows that
$T_W$
, it follows that
![]() $tT_Wt^{-1}$
also has a trivial group of units.
$tT_Wt^{-1}$
also has a trivial group of units.
Remark 7.4. The easy example
![]() $M = {\operatorname {Inv}\bigl \langle {a,b}\:|\:{aba^{-1}b^{-1}=1} \bigr \rangle }$
shows that even in cases where the group of units and the monoid of right units are both finitely presented, it is not the case that the monoid of right units decomposes as the free product of the groups of units and a free (or free inverse) monoid. Indeed, in this example, it can be shown that the group of units is trivial, while the submonoid of right units is isomorphic to the free commutative monoid of rank
$M = {\operatorname {Inv}\bigl \langle {a,b}\:|\:{aba^{-1}b^{-1}=1} \bigr \rangle }$
shows that even in cases where the group of units and the monoid of right units are both finitely presented, it is not the case that the monoid of right units decomposes as the free product of the groups of units and a free (or free inverse) monoid. Indeed, in this example, it can be shown that the group of units is trivial, while the submonoid of right units is isomorphic to the free commutative monoid of rank
![]() $2$
.
$2$
.
Indeed, since
![]() $aba^{-1}b^{-1}$
is cyclically reduced, it follows that the monoid M is E-unitary, hence the submonoid of right units R of M is isomorphic to the submonoid of the group
$aba^{-1}b^{-1}$
is cyclically reduced, it follows that the monoid M is E-unitary, hence the submonoid of right units R of M is isomorphic to the submonoid of the group
![]() $G = {\operatorname {Gp}\bigl \langle {a,b}\:|\:{aba^{-1}b^{-1}=1} \bigr \rangle }$
generated by the prefixes a,
$G = {\operatorname {Gp}\bigl \langle {a,b}\:|\:{aba^{-1}b^{-1}=1} \bigr \rangle }$
generated by the prefixes a,
![]() $ab$
and
$ab$
and
![]() $aba^{-1}=b$
. This is clearly equal to the submonoid of this group generated by
$aba^{-1}=b$
. This is clearly equal to the submonoid of this group generated by
![]() $\{a,b\}$
which has the free commutative monoid of rank 2. The group of units of the free commutative monoid of rank 2 is easily seen to be the trivial group, from which it follows that M has a trivial group of units, as claimed.
$\{a,b\}$
which has the free commutative monoid of rank 2. The group of units of the free commutative monoid of rank 2 is easily seen to be the trivial group, from which it follows that M has a trivial group of units, as claimed.
7.3 A finitely presented special inverse monoid whose group of units is not finitely presented
Another key result due to Makanin (see Theorem 1.2 above) is that the group of units of a finitely presented special monoid is a finitely presented group, with the same number of defining relations. Here, we show that the analogous result does not hold for finitely presented special inverse monoids.
Theorem 7.5. There exists an inverse monoid M defined by a finite special inverse monoid presentation
![]() $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i = 1 \; (i \in I)} \bigr \rangle }$
, such that M has nonfinitely presented group of units G. Moreover, such an example exists where all
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r_i = 1 \; (i \in I)} \bigr \rangle }$
, such that M has nonfinitely presented group of units G. Moreover, such an example exists where all
![]() $r_i$
belong to
$r_i$
belong to
![]() $A^+$
, and so are all cyclically reduced, and M is E-unitary.
$A^+$
, and so are all cyclically reduced, and M is E-unitary.
Proof. It is well known that there exist finitely presented groups which contain finitely generated subgroups that are not finitely presented; for instance, such examples can already be found in the direct product of two free groups [Reference Grunewald10]. In the construction described in Section 6, choose
![]() $Q = \{r_i \::\: i \in I \}$
and
$Q = \{r_i \::\: i \in I \}$
and
![]() $W = \{w_j \::\: j \in J \}$
, such that I and J are finite,
$W = \{w_j \::\: j \in J \}$
, such that I and J are finite,
![]() $W=W^{-1}$
, and such that the subgroup
$W=W^{-1}$
, and such that the subgroup
![]() $H_W$
of
$H_W$
of
![]() $K_Q = {\operatorname {Gp}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
generated by W is not finitely presented. Then by Theorem 6.3 (i), (ii), (v), it follows that
$K_Q = {\operatorname {Gp}\bigl \langle {A}\:|\:{r_i=1 \; (i \in I)} \bigr \rangle }$
generated by W is not finitely presented. Then by Theorem 6.3 (i), (ii), (v), it follows that
![]() $M_{Q,W}$
is an E-unitary finitely presented special inverse monoid with nonfinitely presented group of units
$M_{Q,W}$
is an E-unitary finitely presented special inverse monoid with nonfinitely presented group of units
![]() $U(M_{Q,W})$
. Here,
$U(M_{Q,W})$
. Here,
![]() $U(M_{Q,W}) \cong K_Q \ast H_W$
is not finitely presented since
$U(M_{Q,W}) \cong K_Q \ast H_W$
is not finitely presented since
![]() $H_W$
is not finitely presented and
$H_W$
is not finitely presented and
![]() $H_W$
is a retract of
$H_W$
is a retract of
![]() $K_Q \ast H_W$
. For the last part of the statement, we start from the presentation (30) for
$K_Q \ast H_W$
. For the last part of the statement, we start from the presentation (30) for
![]() $M_{Q,W}$
$M_{Q,W}$
 $$ \begin{align*} M_{Q,W} = \operatorname{Inv}\big\langle {A, t}\:|\: r_i=1 \; (i \in I),\; & a a^{-1} = 1, \; a^{-1} a = 1 \; (a \in A), \\ &\;\quad t w_j t^{-1} t w_j^{-1} t^{-1} = 1, \; t w_j^{-1} t^{-1} t w_j t^{-1} = 1 \; (j \in J) \big\rangle. \end{align*} $$
$$ \begin{align*} M_{Q,W} = \operatorname{Inv}\big\langle {A, t}\:|\: r_i=1 \; (i \in I),\; & a a^{-1} = 1, \; a^{-1} a = 1 \; (a \in A), \\ &\;\quad t w_j t^{-1} t w_j^{-1} t^{-1} = 1, \; t w_j^{-1} t^{-1} t w_j t^{-1} = 1 \; (j \in J) \big\rangle. \end{align*} $$
We then apply a sequence of Tietze transformations on this presentation: we introduce new generators
![]() $t'$
and
$t'$
and
![]() $A'=\{a'\::\: a\in A\}$
, representing
$A'=\{a'\::\: a\in A\}$
, representing
![]() $t^{-1}$
and
$t^{-1}$
and
![]() $\{ a^{-1}\::\: a\in A\}$
, and then replace all occurrences of the inverses by these new generators, to obtain the following presentation for
$\{ a^{-1}\::\: a\in A\}$
, and then replace all occurrences of the inverses by these new generators, to obtain the following presentation for
![]() $M_{Q,W}$
:
$M_{Q,W}$
:
 $$ \begin{align*} \operatorname{Inv}\big\langle {A, A', t, t'}\:|\: \overline{r_i}=1 \; (i \in I), \; a a' = 1, \; & a' a = 1 \; (a \in A), \; t t' = 1, \\ \;&\quad t \overline{w_j} t' t \overline{w_j^{-1}} t' = 1, \; t \overline{w_j^{-1}} t' t \overline{w_j} t' = 1 \; (j \in J) \big\rangle , \end{align*} $$
$$ \begin{align*} \operatorname{Inv}\big\langle {A, A', t, t'}\:|\: \overline{r_i}=1 \; (i \in I), \; a a' = 1, \; & a' a = 1 \; (a \in A), \; t t' = 1, \\ \;&\quad t \overline{w_j} t' t \overline{w_j^{-1}} t' = 1, \; t \overline{w_j^{-1}} t' t \overline{w_j} t' = 1 \; (j \in J) \big\rangle , \end{align*} $$
where
![]() $\overline {v}$
is the word obtained from v by replacing each
$\overline {v}$
is the word obtained from v by replacing each
![]() $a^{-1}$
by
$a^{-1}$
by
![]() $a'$
for
$a'$
for
![]() $a \in A$
. Then this is a finite special inverse presentation for the same monoid
$a \in A$
. Then this is a finite special inverse presentation for the same monoid
![]() $M_{Q,W}$
but with the property that all the defining relators are now strictly positive words.
$M_{Q,W}$
but with the property that all the defining relators are now strictly positive words.
The examples given by this theorem show just how far the Makanin’s result given in Theorem 1.2 is from being true for special inverse monoid presentations.
As explained in the proof of Theorem 7.5, there are well-known examples of finitely presented groups with finitely generated nonfinitely presented subgroups, and the parent group can even be chosen to be a very easy group, namely the direct product of two free groups. The simple nature of these examples makes the process of writing down concrete examples of inverse monoids satisfying the hypothesis of Theorem 7.5 quite straightforward. We do just this in the next example.
Example 7.6. We shall now use the result from [Reference Grunewald10] to write down a concrete example of a finitely presented special inverse monoid with a nonfinitely presented group of units. Let
![]() $K_Q$
be the direct product
$K_Q$
be the direct product
![]() $FG(c_1,c_2) \times FG(d_1,d_2)$
of two free groups of rank
$FG(c_1,c_2) \times FG(d_1,d_2)$
of two free groups of rank
![]() $2$
which has the presentation
$2$
which has the presentation
Let
![]() $\phi : FG(c_1,c_2) \rightarrow FG(t)$
be the surjective homomorphism mapping
$\phi : FG(c_1,c_2) \rightarrow FG(t)$
be the surjective homomorphism mapping
![]() $c_1 \mapsto t$
and
$c_1 \mapsto t$
and
![]() $c_2 \mapsto 1$
, and let
$c_2 \mapsto 1$
, and let
![]() $\psi : FG(d_1,d_2) \rightarrow FG(t)$
be the surjective homomorphism mapping
$\psi : FG(d_1,d_2) \rightarrow FG(t)$
be the surjective homomorphism mapping
![]() $d_1 \mapsto t$
and
$d_1 \mapsto t$
and
![]() $d_2 \mapsto 1$
. Let
$d_2 \mapsto 1$
. Let
Then it follows from Grunewald’s result [Reference Grunewald10] that H is a finitely generated but nonfinitely presented subgroup of
![]() $K_Q$
. In particular, a finite group generating set for H is given by the set
$K_Q$
. In particular, a finite group generating set for H is given by the set
![]() $\{(c_1,d_1), (c_2,1), (1,d_2)\}$
. In terms of the presentation above, these generators are represented by the words
$\{(c_1,d_1), (c_2,1), (1,d_2)\}$
. In terms of the presentation above, these generators are represented by the words
![]() $c_1d_1$
,
$c_1d_1$
,
![]() $c_2$
and
$c_2$
and
![]() $d_2$
, respectively. So if we set
$d_2$
, respectively. So if we set
then
![]() $W = W^{-1}$
, and
$W = W^{-1}$
, and
![]() $K_Q$
and
$K_Q$
and
![]() $H_W$
satisfy the hypotheses in the proof of Theorem 7.5.
$H_W$
satisfy the hypotheses in the proof of Theorem 7.5.
Using this example, the argument in the proof of Theorem 7.5 then shows that if M is the finitely presented special inverse monoid defined by the following finite presentation
 $$ \begin{align*} \mathrm{Inv}{\langle} c_1, c_2, d_1 d_2, t, C_1, C_2, D_1, D_2, T \mid & c_i C_i = 1, \; C_i c_i = 1, & & (i \in \{1,2\}) \\ & d_i D_i = 1, \; D_i d_i = 1 & & (i \in \{1,2\}) \\ & tT=1, \\ & c_id_jC_iD_j=1, & & (i, j \in \{1,2\}), \\ & t c_2 T t C_2 T = 1, & & t C_2 T t c_2 T = 1, \\ & t d_2 T t D_2 T = 1, & & t D_2 T t d_2 T = 1, \\ & t c_1 d_1 T t D_1 C_1 T = 1, & & t D_1 C_1 T t c_1 d_1 T = 1 {\rangle} , \end{align*} $$
$$ \begin{align*} \mathrm{Inv}{\langle} c_1, c_2, d_1 d_2, t, C_1, C_2, D_1, D_2, T \mid & c_i C_i = 1, \; C_i c_i = 1, & & (i \in \{1,2\}) \\ & d_i D_i = 1, \; D_i d_i = 1 & & (i \in \{1,2\}) \\ & tT=1, \\ & c_id_jC_iD_j=1, & & (i, j \in \{1,2\}), \\ & t c_2 T t C_2 T = 1, & & t C_2 T t c_2 T = 1, \\ & t d_2 T t D_2 T = 1, & & t D_2 T t d_2 T = 1, \\ & t c_1 d_1 T t D_1 C_1 T = 1, & & t D_1 C_1 T t c_1 d_1 T = 1 {\rangle} , \end{align*} $$
then the group of units of M is not finitely presented. Note that all the relators in this finite presentation are positive words.
7.4 Group of units finitely presented implies coherence
Recall that a finitely presented group G is said to be coherent if every finitely generated subgroup of G is finitely presented. A well-known question of Baumslag [Reference Baumslag3, page 76] asks whether every one-relator group is coherent. This question remains open in general, but it has recently been shown by Louder and Wilton [Reference Louder and Wilton16], and independently by Wise [Reference Wise28], that all one-relator groups with torsion are coherent.
Given that above we have shown in Theorem 7.1 that the group of units of a special one-relator inverse monoid need not be a one-relator group, and we have shown in Theorem 7.5 that there are finitely presented special inverse monoids with nonfinitely presented groups of units, it is natural to ask whether the group of units of a special one-relator inverse monoid must be finitely presented.
This question remains open, but in the subsection, we present some results which show a close connection between this question and Baumslag’s open problem.
Theorem 7.7. If all one-relator special inverse monoids
![]() $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r = 1} \bigr \rangle }$
have finitely presented groups of units, then all one-relator groups are coherent. In fact, if all E-unitary one-relator special inverse monoids
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r = 1} \bigr \rangle }$
have finitely presented groups of units, then all one-relator groups are coherent. In fact, if all E-unitary one-relator special inverse monoids
![]() $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r = 1} \bigr \rangle }$
have finitely presented groups of units, then all one-relator groups are coherent.
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r = 1} \bigr \rangle }$
have finitely presented groups of units, then all one-relator groups are coherent.
Proof. Suppose there is a one-relator group
![]() $G = {\operatorname {Gp}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
which is not coherent. Set
$G = {\operatorname {Gp}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
which is not coherent. Set
![]() $K_Q = G$
, and let
$K_Q = G$
, and let
![]() $W=A^{-1}$
be a finite subset of
$W=A^{-1}$
be a finite subset of
![]() $F_A$
, such that the subgroup
$F_A$
, such that the subgroup
![]() $H_W$
of G generated by W is not finitely presented. Then Theorem 6.3 (i), (ii), (v) imply that
$H_W$
of G generated by W is not finitely presented. Then Theorem 6.3 (i), (ii), (v) imply that
![]() $M_{Q,W}$
is a one-relator E-unitary special inverse monoid with a nonfinitely presented group of units.
$M_{Q,W}$
is a one-relator E-unitary special inverse monoid with a nonfinitely presented group of units.
Since the group of units of an E-unitary special inverse monoid embeds in the maximal group image, we obtain both directions in that case.
Theorem 7.8. The following are equivalent:
-
(1) All one-relator groups are coherent.
-
(2) Every E-unitary one-relator special inverse monoid
 $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r = 1} \bigr \rangle }$
has a finitely presented group of units.
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r = 1} \bigr \rangle }$
has a finitely presented group of units.
Proof. (ii)
![]() $\Rightarrow $
(i) This follows from Theorem 7.7.
$\Rightarrow $
(i) This follows from Theorem 7.7.
(i)
![]() $\Rightarrow $
(ii) Suppose all one-relator groups are coherent. Then, by Theorem 1.3, given any E-unitary one-relator special inverse monoid
$\Rightarrow $
(ii) Suppose all one-relator groups are coherent. Then, by Theorem 1.3, given any E-unitary one-relator special inverse monoid
![]() $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r = 1} \bigr \rangle }$
, its group of units
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r = 1} \bigr \rangle }$
, its group of units
![]() $U(M)$
is isomorphic to a finitely generated subgroup of the maximal group image
$U(M)$
is isomorphic to a finitely generated subgroup of the maximal group image
![]() ${G = {\operatorname {Gp}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }}$
which is coherent, hence,
${G = {\operatorname {Gp}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }}$
which is coherent, hence,
![]() $U(M)$
is finitely presented.
$U(M)$
is finitely presented.
Combining the argument of (i)
![]() $\Rightarrow $
(ii) from above with the recent result of Louder and Wilton [Reference Louder and Wilton16] and independently Wise [Reference Wise28] that one-relator groups with torsion are coherent, we obtain the following positive result.
$\Rightarrow $
(ii) from above with the recent result of Louder and Wilton [Reference Louder and Wilton16] and independently Wise [Reference Wise28] that one-relator groups with torsion are coherent, we obtain the following positive result.
Theorem 7.9. Let
![]() $M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r^m=1} \bigr \rangle }$
, where
$M = {\operatorname {Inv}\bigl \langle {A}\:|\:{r^m=1} \bigr \rangle }$
, where
![]() $m>1$
,
$m>1$
,
![]() $r \in \overline {A}^{*}$
and M is E-unitary (in particular, this is true if r is a cyclically reduced word). Then the group of units G of M is finitely presented.
$r \in \overline {A}^{*}$
and M is E-unitary (in particular, this is true if r is a cyclically reduced word). Then the group of units G of M is finitely presented.
8 Concluding remarks and open problems
In this section, we list some open problems which naturally arise from the work done in this article.
Question 8.1. Is the group of units of a one-relator inverse monoid
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
finitely presented? How about a torsion one-relator inverse monoid
${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
finitely presented? How about a torsion one-relator inverse monoid
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r^k=1} \bigr \rangle }$
(
${\operatorname {Inv}\bigl \langle {A}\:|\:{r^k=1} \bigr \rangle }$
(
![]() $k>1$
)?
$k>1$
)?
Question 8.2. Do the minimal invertible pieces for
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r^k=1} \bigr \rangle }$
and
${\operatorname {Inv}\bigl \langle {A}\:|\:{r^k=1} \bigr \rangle }$
and
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
coincide?
${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
coincide?
The analogous statement for monoid presentations is true as a consequence of Adjan overlap algorithm. For inverse monoids, it is certainly true that the minimal pieces of
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r^k=1} \bigr \rangle }$
are invertible in
${\operatorname {Inv}\bigl \langle {A}\:|\:{r^k=1} \bigr \rangle }$
are invertible in
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, but it is not clear that the converse is true.
${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, but it is not clear that the converse is true.
Question 8.3. Is the group of units of a one-relator inverse monoid
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
embeddable into a one-relator group?
${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
embeddable into a one-relator group?
Related to this, we have the following question.
Question 8.4. Does the group of units of a one-relator inverse monoid
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
have a soluble word problem?
${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
have a soluble word problem?
Question 8.5. Is every finitely generated subgroup of a one-relator group the group of units of some one-relator inverse monoid?
Question 8.6. Is every finitely generated, recursively presented group the group of units of a finitely presented special inverse monoid?
Question 8.7. The special one-relator inverse monoid counterexamples in Section 7 are all of the form
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, where r is not a reduced word. If we add the hypothesis that r is reduced, or cyclically reduced, is it still possible to construct counterexamples? For example, it is still open whether for every cyclically reduced word r the group of units of
${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
, where r is not a reduced word. If we add the hypothesis that r is reduced, or cyclically reduced, is it still possible to construct counterexamples? For example, it is still open whether for every cyclically reduced word r the group of units of
![]() ${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
is a one-relator group (although we suspect that it is not true).
${\operatorname {Inv}\bigl \langle {A}\:|\:{r=1} \bigr \rangle }$
is a one-relator group (although we suspect that it is not true).
Added in proof. It has recently been announced in [Reference Jaikin-Zapirain and Linton13] that all one-relator groups are coherent. Equivalently, by Theorem 7.8 above, that result shows that every E-unitary one-relator special inverse monoid has a finitely presented group of units. The corresponding question in the non-E-unitary case remains open (see Question 8.1 above).
Funding statement
This research of R. D. Gray was supported by the Engineering and Physical Sciences Research Council projects EP/N033353/1 “Special inverse monoids: subgroups, structure, geometry, rewriting systems and the word problem”, and EP/V032003/1 ‘’Algorithmic, topological and geometric aspects of infinite groups, monoids and inverse semigroups”.
Competing interest
The authors have no competing interest to declare.