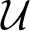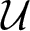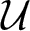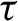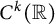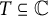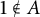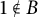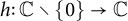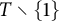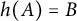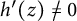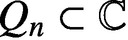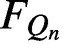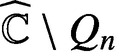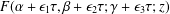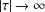46 results in 30Exx
Growth of hypercyclic functions: a continuous path between
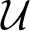 $\mathcal{U}$-frequent hypercyclicity and hypercyclicity
$\mathcal{U}$-frequent hypercyclicity and hypercyclicity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1-36
-
- Article
- Export citation
Inhomogeneous Poisson processes in the disk and interpolation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic expansions relating to the distribution of the length of longest increasing subsequences
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 March 2024, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Karamata's theorem for regularized Cauchy transforms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 January 2024, pp. 1-61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some remarks on approximation in several complex variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 643-653
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Profiling ponded soil surface in saturated seepage into drain-line sink: Kalashnikov’s method of lateral leaching revisited
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 12 July 2022, pp. 367-384
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted cohomological equations for translation flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 22 October 2021, pp. 881-916
- Print publication:
- March 2022
-
- Article
- Export citation
HEDGEHOGS IN LEHMER’S PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 07 September 2021, pp. 236-242
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analytic order-isomorphisms of countable dense subsets of the unit circle
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 July 2021, pp. 653-664
- Print publication:
- September 2022
-
- Article
- Export citation
Asymptotic first boundary value problem for holomorphic functions of several complex variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 361-380
- Print publication:
- June 2022
-
- Article
- Export citation
Peaking and interpolation by complex polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 05 May 2021, pp. 129-138
-
- Article
- Export citation
CARLESON INTERPOLATING SEQUENCES FOR BANACH SPACES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 29 March 2021, pp. 1915-1945
- Print publication:
- November 2022
-
- Article
- Export citation
A VARIANT OF CAUCHY’S ARGUMENT PRINCIPLE FOR ANALYTIC FUNCTIONS WHICH APPLIES TO CURVES CONTAINING ZEROS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 486-492
- Print publication:
- June 2021
-
- Article
- Export citation
Mixing operators with prescribed unimodular eigenvalues
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 1-8
- Print publication:
- January 2022
-
- Article
- Export citation
STARLIKENESS AND CONVEXITY OF CAUCHY TRANSFORMS ON REGULAR POLYGONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 291-302
- Print publication:
- April 2021
-
- Article
- Export citation
INTEGRAL MEANS OF UNIVALENT FUNCTIONS ON AN ANNULUS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 September 2020, p. 512
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
ASYMPTOTICS OF A GAUSS HYPERGEOMETRIC FUNCTION WITH TWO LARGE PARAMETERS: A NEW CASE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 446-452
-
- Article
- Export citation
Universal Entire Functions That Define Order Isomorphisms of Countable Real Sets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 10 April 2019, pp. 767-779
- Print publication:
- December 2019
-
- Article
- Export citation
Explicit asymptotics for certain single and double exponential sums
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 22 January 2019, pp. 607-632
- Print publication:
- April 2020
-
- Article
- Export citation
Approximating the Riemann Zeta-function by Polynomials with Restricted Zeros
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 475-478
- Print publication:
- September 2019
-
- Article
- Export citation