No CrossRef data available.
Article contents
STARLIKENESS AND CONVEXITY OF CAUCHY TRANSFORMS ON REGULAR POLYGONS
Published online by Cambridge University Press: 05 October 2020
Abstract
For 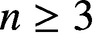 $n\geq 3$
, let
$n\geq 3$
, let 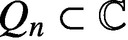 $Q_n\subset \mathbb {C}$
be an arbitrary regular n-sided polygon. We prove that the Cauchy transform
$Q_n\subset \mathbb {C}$
be an arbitrary regular n-sided polygon. We prove that the Cauchy transform 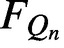 $F_{Q_n}$
of the normalised two-dimensional Lebesgue measure on
$F_{Q_n}$
of the normalised two-dimensional Lebesgue measure on 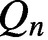 $Q_n$
is univalent and starlike but not convex in
$Q_n$
is univalent and starlike but not convex in 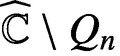 $\widehat {\mathbb {C}}\setminus Q_n$
.
$\widehat {\mathbb {C}}\setminus Q_n$
.
- Type
- Research Article
- Information
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
Footnotes
This research is supported in part by the NNSF of China (No. 11831007).





