Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-26T07:19:21.221Z Has data issue: false hasContentIssue false
  • English
  • Français

ASYMPTOTICS OF A GAUSS HYPERGEOMETRIC FUNCTION WITH TWO LARGE PARAMETERS: A NEW CASE

Part of: Miscellaneous topics of analysis in the complex domain

Published online by Cambridge University Press:  10 December 2019

J. F. HARPER Open the ORCID record for J. F. HARPER [Opens in a new window]
J. F. HARPER*
Affiliation:
School of Mathematics and Statistics, Victoria University of Wellington, PO Box 600, Wellington6140, New Zealand; e-mail: john.harper@vuw.ac.nz
Get access Rights & Permissions [Opens in a new window]

Abstract

Asymptotic expansions of the Gauss hypergeometric function with large parameters, 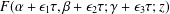$F(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D716}_{2}\unicode[STIX]{x1D70F};\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D716}_{3}\unicode[STIX]{x1D70F};z)$ as 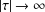$|\unicode[STIX]{x1D70F}|\rightarrow \infty$, are known for many special cases, but not for one that the author encountered in recent work on fluid mechanics: 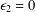$\unicode[STIX]{x1D716}_{2}=0$ and 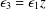$\unicode[STIX]{x1D716}_{3}=\unicode[STIX]{x1D716}_{1}z$. This paper gives the leading term for that case if 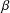$\unicode[STIX]{x1D6FD}$ is not a negative integer and $z$ is not on the branch cut 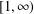$[1,\infty )$, and it shows how subsequent terms can be found.

Keywords

asymptotic expansionshypergeometric functionslarge parameters

MSC classification

Primary: 30E15: Asymptotic representations in the complex domain
Secondary: 33C05: Classical hypergeometric functions, $_2F_1$
Type
Research Article
Information
The ANZIAM Journal , Volume 62 , Issue 4 , October 2020 , pp. 446 - 452
Check for updates
Copyright
© Australian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A., Handbook of mathematical functions (Dover, New York, 1972) ISBN: 100486612724.Google Scholar
Cvitković, M., Smith, A.-S. and Pande, J., “Asymptotic expansions of the hypergeometric function with two large parameters—application to the partition function of a lattice gas in a field of traps”, J. Phys. A 50 (2017) 265206; doi:10.1088/1751-8121/aa7213.Google Scholar
Harper, J. F., “Effect of a negatively surface-active solute on a bubble rising in a liquid”, Quart. J. Mech. Appl. Math. 71 (2018) 427–439; doi:10.1093/qjmam/hby012.Google Scholar
Nemes, G., “An explicit formula for the coefficients in Laplace’s method”, Constr. Approx. 38 (2013) 471–487; doi:10.1007/s00365-013-9202-6.CrossRefGoogle Scholar
Olver, F. W. J., Lozier, D. W., Boisvert, R. F. and Clark, C. W. (eds), NIST handbook of mathematical functions (Cambridge University Press, Cambridge, 2010) ISBN: 978-0-521-19225-5.Google Scholar
Paris, R. B., “Asymptotics of the Gauss hypergeometric function with large parameters, I”, J. Class. Anal. 2 (2013) 183–203; doi:10.7153/jca-02-15.Google Scholar
Paris, R. B., “Asymptotics of the Gauss hypergeometric function with large parameters, II”, J. Class. Anal. 3 (2013) 1–15; doi:10.7153/jca-03-01.Google Scholar
Watson, G. N., “Asymptotic expansions of hypergeometric functions”, Trans. Cambridge Philos. Soc. 22 (1918) 277–308.Google Scholar
Wojdylo, J., “On the coefficients that arise from Laplace’s method”, J. Comput. Appl. Math. 196 (2006) 241–266; doi:10.1016/j.cam.2005.09.004.CrossRefGoogle Scholar
Wojdylo, J., “Computing the coefficients in Laplace’s method”, SIAM Rev. 48 (2006) 76–96; doi:10.1137/S0036144504446175.CrossRefGoogle Scholar