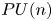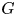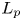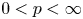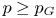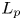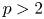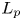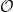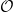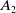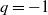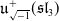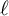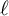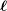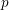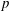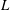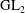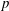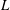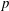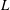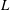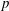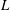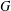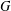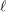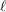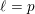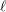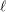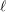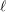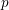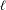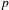56 results
Torsion in classifying spaces of gauge groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isometric actions on Lp-spaces: dependence on the value of p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1300-1313
- Print publication:
- June 2023
-
- Article
- Export citation
Cohomology in singular blocks of parabolic category
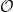 $\mathcal{O}$
$\mathcal{O}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 555-568
- Print publication:
- September 2023
-
- Article
- Export citation
Integral Fourier transforms and the integral Hodge conjecture for one-cycles on abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1188-1213
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived homotopy algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 25 July 2022, pp. 1198-1243
- Print publication:
- August 2023
-
- Article
- Export citation
On the computation of Hopf 2-cocycles with an example of diagonal type
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 141-169
- Print publication:
- January 2023
-
- Article
- Export citation
ACTIONS OF MONOIDAL CATEGORIES AND REPRESENTATIONS OF CARTAN TYPE LIE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 22 February 2022, pp. 2367-2402
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE GENERIC FIBRE OF MODULI SPACES OF BOUNDED LOCAL G-SHTUKAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 July 2021, pp. 799-878
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomology of fiber-bunched twisted cocycles over hyperbolic systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 844-860
-
- Article
- Export citation
Corrigendum: Around
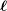 $\boldsymbol{\ell }$-independence
$\boldsymbol{\ell }$-independence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 29 May 2020, pp. 1262-1274
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
RIGIDIFIED TORSOR COCYCLES, HYPERCOVERINGS AND BUNDLE GERBES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 April 2020, pp. 115-144
- Print publication:
- February 2022
-
- Article
- Export citation
Introduction
-
- Book:
- Foundations of Stable Homotopy Theory
- Published online:
- 09 March 2020
- Print publication:
- 26 March 2020, pp 1-6
-
- Chapter
- Export citation

Foundations of Stable Homotopy Theory
-
- Published online:
- 09 March 2020
- Print publication:
- 26 March 2020
tt-geometry of Tate motives over algebraically closed fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 10 / October 2019
- Published online by Cambridge University Press:
- 06 September 2019, pp. 1888-1923
- Print publication:
- October 2019
-
- Article
- Export citation
The Cohomology Groups of Real Toric Varieties Associated with Weyl Chambers of Types C and D
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 14 February 2019, pp. 861-874
-
- Article
- Export citation
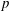 $p$-adic
$p$-adic 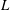 $L$-functions for
$L$-functions for 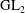 $\text{GL}_{2}$
$\text{GL}_{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1019-1059
- Print publication:
- October 2019
-
- Article
- Export citation
A VON NEUMANN ALGEBRA CHARACTERIZATION OF PROPERTY (T) FOR GROUPOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 363-386
- Print publication:
- June 2020
-
- Article
- Export citation
COHOMOLOGY OF FILIFORM LIE ALGEBRAS OVER FIELDS OF CHARACTERISTIC TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 168-170
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Around
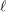 $\ell$-independence
$\ell$-independence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 223-248
- Print publication:
- January 2018
-
- Article
-
- You have access
- HTML
- Export citation
ON THE COHOMOLOGY OF SOME SIMPLE SHIMURA VARIETIES WITH BAD REDUCTION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 06 December 2016, pp. 1-24
- Print publication:
- January 2019
-
- Article
- Export citation