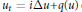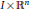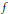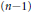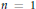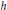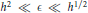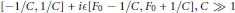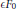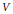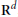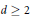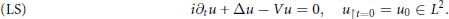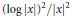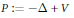21 results
Dispersive and Strichartz estimates for 3D wave equation with a Laguerre potential
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-28
-
- Article
- Export citation
Stable solutions to double phase problems involving a nonlocal term
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1119-1141
-
- Article
- Export citation
Quantum systems at the brink: existence of bound states, critical potentials, and dimensionality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 July 2023, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomial stability of a piezoelectric beam with magnetic effect and a boundary dissipation of the fractional derivative type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 05 April 2023, pp. 23-53
-
- Article
- Export citation
STABLE SOLUTIONS TO THE STATIC CHOQUARD EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 10 June 2020, pp. 471-478
- Print publication:
- December 2020
-
- Article
- Export citation
Spectral transitions for Aharonov-Bohm Laplacians on conical layers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1663-1687
- Print publication:
- December 2019
-
- Article
- Export citation
The time-dependent Schrödinger equation with piecewise constant potentials
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 57-83
-
- Article
- Export citation
The initial-value problem for a fourth-order dispersive closed curve flow on the 2-sphere
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1243-1277
- Print publication:
- December 2017
-
- Article
- Export citation
Fast Evaluation of the Caputo Fractional Derivative and its Applications to Fractional Diffusion Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 650-678
- Print publication:
- March 2017
-
- Article
- Export citation
Accurate and Efficient Numerical Methods for Computing Ground States and Dynamics of Dipolar Bose-Einstein Condensates via the Nonuniform FFT
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1141-1166
- Print publication:
- May 2016
-
- Article
- Export citation
Computing the Ground and First Excited States of the Fractional Schrödinger Equation in an Infinite Potential Well
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 2 / August 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 321-350
- Print publication:
- August 2015
-
- Article
- Export citation
Local Discontinuous Galerkin Methods for the 2D Simulation of Quantum Transport Phenomena on Quantum Directional Coupler
-
- Journal:
- Communications in Computational Physics / Volume 15 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1012-1028
- Print publication:
- April 2014
-
- Article
- Export citation
Linear Scaling Discontinuous Galerkin Density Matrix Minimization Method with Local Orbital Enriched Finite Element Basis: 1-D Lattice Model System
-
- Journal:
- Communications in Computational Physics / Volume 14 / Issue 2 / August 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 276-300
- Print publication:
- August 2013
-
- Article
- Export citation
A Numerical Study of Quantum Decoherence
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 1 / July 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 85-108
- Print publication:
- July 2012
-
- Article
- Export citation
A Finite Volume Method for the Multi Subband Boltzmann Equation with Realistic 2D Scattering in Double Gate MOSFETs
-
- Journal:
- Communications in Computational Physics / Volume 10 / Issue 2 / August 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 305-338
- Print publication:
- August 2011
-
- Article
- Export citation
Short Time Behavior of Solutions to Linear and Nonlinear Schrödinger Equations
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 5 / October 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1168-1200
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Non-Selfadjoint Perturbations of Selfadjoint Operators in Two Dimensions IIIa. One Branching Point
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 3 / 01 June 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 572-657
- Print publication:
- 01 June 2008
-
- Article
-
- You have access
- Export citation
A Singular Critical Potential for the Schrödinger Operator
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 1 / 01 March 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 35-47
- Print publication:
- 01 March 2007
-
- Article
-
- You have access
- Export citation
SEMICLASSICAL ANALYSIS FOR MAGNETIC SCATTERING BY TWO SOLENOIDAL FIELDS
-
- Journal:
- Journal of the London Mathematical Society / Volume 74 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 04 January 2007, pp. 695-716
- Print publication:
- December 2006
-
- Article
- Export citation
Imprimitively Generated Lie-Algebraic Hamiltonians and Separation of Variables
-
- Journal:
- Canadian Journal of Mathematics / Volume 50 / Issue 6 / 01 December 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1298-1322
- Print publication:
- 01 December 1998
-
- Article
-
- You have access
- Export citation



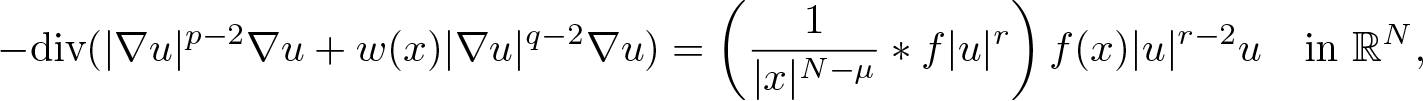
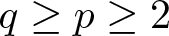
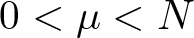
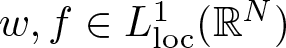
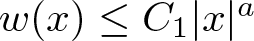
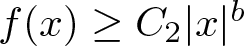
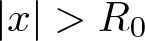
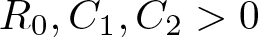
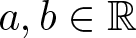
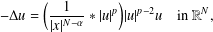
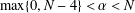
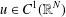
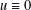
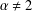
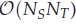 memory and
memory and  work, where
work, where 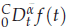 of order
of order 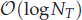 for
for 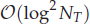 for
for 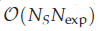 storage and
storage and 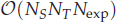 work when numerically solving the time fractional PDEs. Furthermore, we also give the stability and error analysis of the new scheme, and present several numerical examples to demonstrate the performance of our scheme.
work when numerically solving the time fractional PDEs. Furthermore, we also give the stability and error analysis of the new scheme, and present several numerical examples to demonstrate the performance of our scheme.