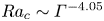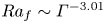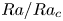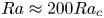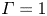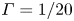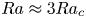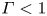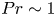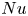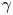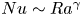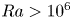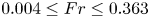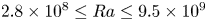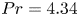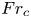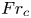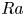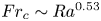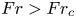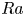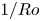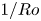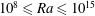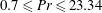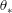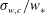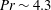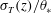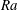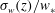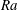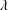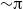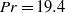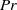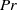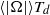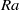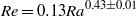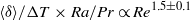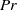12 results
Transition to fully developed turbulence in liquid-metal convection facilitated by spatial confinement
-
- Journal:
- Journal of Fluid Mechanics / Volume 981 / 25 February 2024
- Published online by Cambridge University Press:
- 23 February 2024, R2
-
- Article
- Export citation
Strong coupling of flow structure and heat transport in liquid metal thermal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 975 / 25 November 2023
- Published online by Cambridge University Press:
- 17 November 2023, A21
-
- Article
- Export citation
Dissociation between neuroanatomical and symptomatic subtypes in schizophrenia
-
- Journal:
- European Psychiatry / Volume 66 / Issue 1 / 2023
- Published online by Cambridge University Press:
- 13 September 2023, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Foreground-background salience effect in traffic risk communication
-
- Journal:
- Judgment and Decision Making / Volume 9 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 01 January 2023, pp. 83-89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flow states and heat transport in liquid metal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 951 / 25 November 2022
- Published online by Cambridge University Press:
- 28 October 2022, R1
-
- Article
-
- You have access
- HTML
- Export citation
On the centrifugal effect in turbulent rotating thermal convection: onset and heat transport
-
- Journal:
- Journal of Fluid Mechanics / Volume 938 / 10 May 2022
- Published online by Cambridge University Press:
- 21 March 2022, R1
-
- Article
- Export citation
Universal fluctuations in the bulk of Rayleigh–Bénard turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 878 / 10 November 2019
- Published online by Cambridge University Press:
- 06 September 2019, R1
-
- Article
- Export citation
Turbulent thermal convection over rough plates with varying roughness geometries
-
- Journal:
- Journal of Fluid Mechanics / Volume 825 / 25 August 2017
- Published online by Cambridge University Press:
- 21 July 2017, pp. 573-599
-
- Article
- Export citation
Interfacial Complexions and the Related Atomic Transport Behaviors in Gold-Oxide Systems
-
- Journal:
- Microscopy and Microanalysis / Volume 22 / Issue S3 / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 1906-1907
- Print publication:
- July 2016
-
- Article
-
- You have access
- Export citation
Effects of polymer additives in the bulk of turbulent thermal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 784 / 10 December 2015
- Published online by Cambridge University Press:
- 04 November 2015, R3
-
- Article
- Export citation
Dynamics and flow coupling in two-layer turbulent thermal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 728 / 10 August 2013
- Published online by Cambridge University Press:
- 05 July 2013, R1
-
- Article
- Export citation
Dynamics of the large-scale circulation in high-Prandtl-number turbulent thermal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 717 / 25 February 2013
- Published online by Cambridge University Press:
- 01 February 2013, pp. 322-346
-
- Article
- Export citation