Article contents
Dynamics and flow coupling in two-layer turbulent thermal convection
Published online by Cambridge University Press: 05 July 2013
Abstract
We present an experimental investigation of the dynamics and flow coupling of convective turbulent flows in a cylindrical Rayleigh–Bénard convection (RBC) cell with two immiscible fluids, water and Fluorinert FC-77 electronic liquid (FC77). With the lighter water above FC77, the latter is under the condition of constant heat flux at its top and bottom boundaries. It is found that one large-scale circulation (LSC) roll exists in each of the fluid layers, and that their circulation planes have two preferred azimuthal orientations separated by 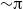 ${\sim }\mathrm{\pi} $. A surprising finding of the study is that cessations/reversals of the LSC in FC77 of the two-layer system occur much more frequently than they do in single-layer turbulent RBC, and that a cessation is most likely to result in a flow reversal of the LSC, which is in sharp contrast with the uniform distribution of the orientational angular change of the LSC before and after cessations in single-layer turbulent RBC. This implies that the dynamics governing cessations and reversals in the two systems are very different. Two coupling modes, thermal coupling (the flow directions of the two LSCs are opposite to each other at the fluid–fluid interface) and viscous coupling (the flow directions of the two LSCs are the same at the fluid–fluid interface), are identified, with the former as the predominant mode. That most cessations (in the FC77 layer) end up as reversals can be understood as a symmetry breaking imposed by the orientation of the LSC in the water layer, which remains unchanged most of the time. Furthermore, the frequently occurring cessations and reversals are caused by the system switching between its two metastable states, i.e. thermal and viscous coupling modes. It is also observed that the strength of the LSC in water becomes weaker when the LSC in FC77 rotates faster azimuthally and that the flow strength in FC77 becomes stronger when the LSC in water rotates faster azimuthally, i.e. the influence of the LSC in one fluid layer on the other is not symmetric.
${\sim }\mathrm{\pi} $. A surprising finding of the study is that cessations/reversals of the LSC in FC77 of the two-layer system occur much more frequently than they do in single-layer turbulent RBC, and that a cessation is most likely to result in a flow reversal of the LSC, which is in sharp contrast with the uniform distribution of the orientational angular change of the LSC before and after cessations in single-layer turbulent RBC. This implies that the dynamics governing cessations and reversals in the two systems are very different. Two coupling modes, thermal coupling (the flow directions of the two LSCs are opposite to each other at the fluid–fluid interface) and viscous coupling (the flow directions of the two LSCs are the same at the fluid–fluid interface), are identified, with the former as the predominant mode. That most cessations (in the FC77 layer) end up as reversals can be understood as a symmetry breaking imposed by the orientation of the LSC in the water layer, which remains unchanged most of the time. Furthermore, the frequently occurring cessations and reversals are caused by the system switching between its two metastable states, i.e. thermal and viscous coupling modes. It is also observed that the strength of the LSC in water becomes weaker when the LSC in FC77 rotates faster azimuthally and that the flow strength in FC77 becomes stronger when the LSC in water rotates faster azimuthally, i.e. the influence of the LSC in one fluid layer on the other is not symmetric.
JFM classification
- Type
- Rapids
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 14
- Cited by




