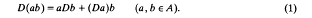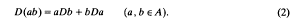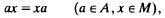16 results
On Positive Definiteness Over Locally Compact Quantum Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 5 / 01 October 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1067-1095
- Print publication:
- 01 October 2016
-
- Article
-
- You have access
- Export citation
Norm One Idempotent cb-Multipliers with Applications to the Fourier Algebra in the cb-Multiplier Norm
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 4 / 01 December 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 654-662
- Print publication:
- 01 December 2011
-
- Article
-
- You have access
- Export citation
CO-REPRESENTATIONS OF HOPF–VON NEUMANN ALGEBRAS ON OPERATOR SPACES OTHER THAN COLUMN HILBERT SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 205-210
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Local spectral properties of convolution operators on non-abelian groups
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 39 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 20 January 2009, pp. 143-149
-
- Article
-
- You have access
- Export citation
Operator Amenability of the Fourier Algebra in the cb-Multiplier Norm
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 5 / 01 October 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 966-980
- Print publication:
- 01 October 2007
-
- Article
-
- You have access
- Export citation
Operator amenability of Fourier–Stieltjes algebras
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 136 / Issue 3 / May 2004
- Published online by Cambridge University Press:
- 21 April 2004, pp. 675-686
- Print publication:
- May 2004
-
- Article
- Export citation
The Operator Amenability of Uniform Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 4 / 01 December 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 632-634
- Print publication:
- 01 December 2003
-
- Article
-
- You have access
- Export citation
Connes-amenability and normal, virtual diagonals for measure algebras, II
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 68 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 17 April 2009, pp. 325-328
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
CONNES-AMENABILITY AND NORMAL, VIRTUAL DIAGONALS FOR MEASURE ALGEBRAS I
-
- Journal:
- Journal of the London Mathematical Society / Volume 67 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 20 May 2003, pp. 643-656
- Print publication:
- June 2003
-
- Article
- Export citation
Automatic continuity and second order cohomology
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 231-243
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
DERIVATIONS ON GROUP ALGEBRAS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 80 / Issue 2 / March 2000
- Published online by Cambridge University Press:
- 01 March 2000, pp. 360-390
- Print publication:
- March 2000
-
- Article
- Export citation
Topologically simple Banach algebras with derivation
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 60 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 17 April 2009, pp. 153-161
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
INTERTWINING MAPS FROM CERTAIN GROUP ALGEBRAS
-
- Journal:
- Journal of the London Mathematical Society / Volume 57 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 01 April 1998, pp. 433-448
- Print publication:
- April 1998
-
- Article
- Export citation
Discontinuous homomorphisms from Banach *-algebras
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 120 / Issue 4 / November 1996
- Published online by Cambridge University Press:
- 24 October 2008, pp. 703-708
- Print publication:
- November 1996
-
- Article
- Export citation
The structure of discontinuous homomorphisms from non-commutative C*-algebras
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 209-218
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
A functorial approach to weak amenability for commutative Banach algebras
-
- Journal:
- Glasgow Mathematical Journal / Volume 34 / Issue 2 / May 1992
- Published online by Cambridge University Press:
- 18 May 2009, pp. 241-251
- Print publication:
- May 1992
-
- Article
-
- You have access
- Export citation




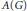
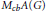
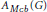
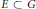

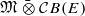 is a Banach algebra if and only if 𝔐 is subhomogeneous or
is a Banach algebra if and only if 𝔐 is subhomogeneous or 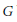
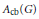
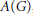
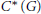
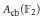
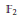
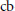
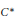
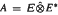 , where
, where 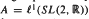 . An important rôle is played by the second Hochschild cohomology group of
. An important rôle is played by the second Hochschild cohomology group of 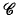 (
(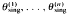 :
: 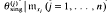
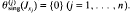 is a homomorphism, and
is a homomorphism, and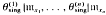
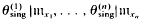 to map into rad(
to map into rad(