Article contents
Norm One Idempotent cb-Multipliers with Applications to the Fourier Algebra in the cb-Multiplier Norm
Published online by Cambridge University Press: 20 November 2018
Abstract
For a locally compact group  $G$, let
$G$, let 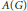 $A(G)$ be its Fourier algebra, let
$A(G)$ be its Fourier algebra, let  ${{M}_{cb}}A(G)$ denote the completely bounded multipliers of
${{M}_{cb}}A(G)$ denote the completely bounded multipliers of 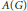 $A(G)$, and let
$A(G)$, and let 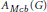 ${{A}_{Mcb}}\,(G)$ stand for the closure of
${{A}_{Mcb}}\,(G)$ stand for the closure of 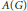 $A(G)$ in
$A(G)$ in  ${{M}_{cb}}A(G)$. We characterize the norm one idempotents in
${{M}_{cb}}A(G)$. We characterize the norm one idempotents in  ${{M}_{cb}}A(G)$: the indicator function of a set
${{M}_{cb}}A(G)$: the indicator function of a set 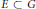 $E\,\subset \,G$ is a norm one idempotent in
$E\,\subset \,G$ is a norm one idempotent in  ${{M}_{cb}}A(G)$ if and only if
${{M}_{cb}}A(G)$ if and only if  $E$ is a coset of an open subgroup of
$E$ is a coset of an open subgroup of  $G$. As applications, we describe the closed ideals of
$G$. As applications, we describe the closed ideals of 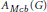 ${{A}_{Mcb}}\,(G)$ with an approximate identity bounded by 1, and we characterize those
${{A}_{Mcb}}\,(G)$ with an approximate identity bounded by 1, and we characterize those  $G$ for which
$G$ for which 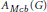 ${{A}_{Mcb}}\,(G)$ is 1-amenable in the sense of B. E. Johnson. (We can even slightly relax the norm bounds.)
${{A}_{Mcb}}\,(G)$ is 1-amenable in the sense of B. E. Johnson. (We can even slightly relax the norm bounds.)
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011
References
- 5
- Cited by


