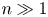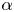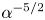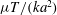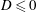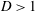110 results
Shallow current of viscous fluid flowing between diverging or converging walls
-
- Journal:
- Journal of Fluid Mechanics / Volume 977 / 25 December 2023
- Published online by Cambridge University Press:
- 15 December 2023, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Axisymmetric column collapses of bi-frictional granular mixtures
-
- Journal:
- Journal of Fluid Mechanics / Volume 963 / 25 May 2023
- Published online by Cambridge University Press:
- 12 May 2023, A4
-
- Article
- Export citation
The fate of continuous input of relatively heavy fluid at the base of a porous medium
-
- Journal:
- Journal of Fluid Mechanics / Volume 932 / 10 February 2022
- Published online by Cambridge University Press:
- 02 December 2021, A5
-
- Article
- Export citation
Viscous gravity currents over flat inclined surfaces
-
- Journal:
- Journal of Fluid Mechanics / Volume 931 / 25 January 2022
- Published online by Cambridge University Press:
- 23 November 2021, A12
-
- Article
- Export citation
Steady-state mushy layers: experiments and theory
-
- Journal:
- Journal of Fluid Mechanics / Volume 570 / 10 January 2007
- Published online by Cambridge University Press:
- 14 October 2021, pp. 69-77
-
- Article
- Export citation
Spreading or contraction of viscous drops between plates: single, multiple or annular drops
-
- Journal:
- Journal of Fluid Mechanics / Volume 925 / 25 October 2021
- Published online by Cambridge University Press:
- 26 August 2021, A26
-
- Article
- Export citation
Viscous backflow from a model fracture network: influence of a permeable boundary
-
- Journal:
- Journal of Fluid Mechanics / Volume 911 / 25 March 2021
- Published online by Cambridge University Press:
- 01 February 2021, A42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interaction of viscous free-surface flows with topography
-
- Journal:
- Journal of Fluid Mechanics / Volume 876 / 10 October 2019
- Published online by Cambridge University Press:
- 08 August 2019, pp. 912-938
-
- Article
- Export citation
Similarity solutions and viscous gravity current adjustment times
-
- Journal:
- Journal of Fluid Mechanics / Volume 874 / 10 September 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 285-298
-
- Article
- Export citation
Backflow from a model fracture network: an asymptotic investigation
-
- Journal:
- Journal of Fluid Mechanics / Volume 864 / 10 April 2019
- Published online by Cambridge University Press:
- 14 February 2019, pp. 899-924
-
- Article
- Export citation
Flow of buoyant granular materials along a free surface
-
- Journal:
- Journal of Fluid Mechanics / Volume 848 / 10 August 2018
- Published online by Cambridge University Press:
- 04 June 2018, pp. 312-339
-
- Article
- Export citation
Experimental exploration of fluid-driven cracks in brittle hydrogels
-
- Journal:
- Journal of Fluid Mechanics / Volume 844 / 10 June 2018
- Published online by Cambridge University Press:
- 12 April 2018, pp. 435-458
-
- Article
- Export citation
Dynamics of viscous backflow from a model fracture network
-
- Journal:
- Journal of Fluid Mechanics / Volume 836 / 10 February 2018
- Published online by Cambridge University Press:
- 12 December 2017, pp. 828-849
-
- Article
- Export citation
Two-phase gravity currents resulting from the release of a fixed volume of fluid in a porous medium
-
- Journal:
- Journal of Fluid Mechanics / Volume 832 / 10 December 2017
- Published online by Cambridge University Press:
- 26 October 2017, pp. 550-577
-
- Article
- Export citation
The relaxation time for viscous and porous gravity currents following a change in flux
-
- Journal:
- Journal of Fluid Mechanics / Volume 821 / 25 June 2017
- Published online by Cambridge University Press:
- 24 May 2017, pp. 330-342
-
- Article
- Export citation
Inclined gravity currents filling basins: the impact of peeling detrainment on transport and vertical structure
-
- Journal:
- Journal of Fluid Mechanics / Volume 820 / 10 June 2017
- Published online by Cambridge University Press:
- 05 May 2017, pp. 400-423
-
- Article
- Export citation
The Physical Processes involved in the Melting of Icebergs (Invited paper)
-
- Journal:
- Annals of Glaciology / Volume 1 / 1980
- Published online by Cambridge University Press:
- 20 January 2017, pp. 97-101
-
- Article
-
- You have access
- HTML
- Export citation
Compressible vapour flow in conduits and fractures
-
- Journal:
- Journal of Fluid Mechanics / Volume 802 / 10 September 2016
- Published online by Cambridge University Press:
- 10 August 2016, pp. 750-759
-
- Article
- Export citation
Stratified gravity currents in porous media
-
- Journal:
- Journal of Fluid Mechanics / Volume 791 / 25 March 2016
- Published online by Cambridge University Press:
- 22 February 2016, pp. 329-357
-
- Article
- Export citation
Fluid invasion of an unsaturated leaky porous layer
-
- Journal:
- Journal of Fluid Mechanics / Volume 777 / 25 August 2015
- Published online by Cambridge University Press:
- 21 July 2015, pp. 97-121
-
- Article
- Export citation