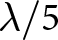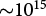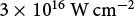897 results
Multipronged strategy for protection and motivation of healthcare workers during the COVID-19 pandemic: a real-life study
-
- Journal:
- Antimicrobial Stewardship & Healthcare Epidemiology / Volume 4 / Issue 1 / 2024
- Published online by Cambridge University Press:
- 25 July 2024, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
10 - Sustainable Development Goal Indicators on Maternal Health and Socio-Economic Inequalities in India
-
-
- Book:
- India Population Report
- Published online:
- 15 August 2023
- Print publication:
- 27 June 2024, pp 347-388
-
- Chapter
- Export citation
4 - Mortality and Epidemiological Transition
-
-
- Book:
- India Population Report
- Published online:
- 15 August 2023
- Print publication:
- 27 June 2024, pp 110-170
-
- Chapter
- Export citation
Impacts of soil and water conservation measures on farm technical efficiency in the semi-arid tropics of central India
-
- Journal:
- Environmental Conservation , First View
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-8
-
- Article
- Export citation
P.027 KNOW BRAIN EMBRACE CARE: A study investigating young adult stroke patients’ knowledge and behaviour around lifestyle
-
- Journal:
- Canadian Journal of Neurological Sciences / Volume 51 / Issue s1 / June 2024
- Published online by Cambridge University Press:
- 24 May 2024, p. S22
-
- Article
-
- You have access
- Export citation
Expert Consensus Statement for Telepsychiatry and Attention Deficit Hyperactivity Disorder
-
- Journal:
- CNS Spectrums / Accepted manuscript
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-34
-
- Article
- Export citation
High-gain TM11 mode equilateral triangular patch antenna with shorting pins and triangular short horn
-
- Journal:
- International Journal of Microwave and Wireless Technologies , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-15
-
- Article
- Export citation
Hot electron emission characteristics from thin metal foil targets irradiated by terawatt laser
-
- Journal:
- Laser and Particle Beams / Volume 42 / 2024
- Published online by Cambridge University Press:
- 17 April 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mechanism for axial pattern formation of concentrated suspension in a horizontal rotating cylinder
-
- Journal:
- Journal of Fluid Mechanics / Volume 985 / 25 April 2024
- Published online by Cambridge University Press:
- 16 April 2024, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radiocarbon Dates from the Archaeological Site of Sakas, Bihar, India
-
- Journal:
- Radiocarbon / Volume 66 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 29 April 2024, pp. 267-279
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DNA methylation in necrotizing enterocolitis
-
- Journal:
- Expert Reviews in Molecular Medicine / Volume 26 / 2024
- Published online by Cambridge University Press:
- 01 April 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Head and Neck Cancer: United Kingdom National Multidisciplinary Guidelines, Sixth Edition
-
- Journal:
- The Journal of Laryngology & Otology / Volume 138 / Issue S1 / April 2024
- Published online by Cambridge University Press:
- 14 March 2024, pp. S1-S224
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITENESS OF CANONICAL QUOTIENTS OF DEHN QUANDLES OF SURFACES
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-18
-
- Article
- Export citation
Impact of universal chlorhexidine bathing with or without COVID-19 intensive training on staff and resident COVID-19 case rates in nursing homes
-
- Journal:
- Infection Control & Hospital Epidemiology , First View
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-4
-
- Article
- Export citation
Metrology for sub-Rayleigh-length target positioning in ~1022 W/cm2 laser-plasma experiments
-
- Journal:
- High Power Laser Science and Engineering / Accepted manuscript
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-58
-
- Article
-
- You have access
- Open access
- Export citation
Influence of Citric Acid and Glycine on the Adsorption of Mercury (II) by Kaolinite under Various pH Conditions
-
- Journal:
- Clays and Clay Minerals / Volume 44 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 28 February 2024, pp. 41-48
-
- Article
- Export citation
High touch surface bioburden associated with the use of disinfectants with and without continuously active disinfection in ambulatory care settings
-
- Journal:
- Infection Control & Hospital Epidemiology / Volume 45 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 20 February 2024, pp. 790-792
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polarization insensitive passive loaded wideband metamaterial absorber
-
- Journal:
- International Journal of Microwave and Wireless Technologies , First View
- Published online by Cambridge University Press:
- 08 February 2024, pp. 1-9
-
- Article
- Export citation
Diagnostic stewardship to improve patient outcomes and healthcare-associated infection (HAI) metrics
- Part of
-
- Journal:
- Infection Control & Hospital Epidemiology / Volume 45 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 405-411
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantifying racial disparities in risk of invasive Staphylococcus aureus infection in Metropolitan Atlanta, Georgia, during the 2020–2021 coronavirus disease 2019 (COVID-19) pandemic
-
- Journal:
- Infection Control & Hospital Epidemiology / Volume 45 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 534-536
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation