No CrossRef data available.
High-gain TM11 mode equilateral triangular patch antenna with shorting pins and triangular short horn
Published online by Cambridge University Press: 10 May 2024
Abstract
Normally, the reported gain of the microstrip patch antenna is within 8 dBi. Using properly located three shorting pins on three bisectors, the present work reports a method to convert the non-radiating TM11 mode of equilateral triangular patch antennas (ETPAs) to a deformed TM11 radiating mode. The boresight gain of ETPA operating in TM11 mode is enhanced from −10.75 to 12.1 dBi at 5.43 GHz. The boresight measured gain is further enhanced to 14.2 dBi at 5.52 GHz by using a triangular surface-mounted short horn (SMSH) of about 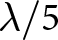 ${{\lambda }}/5$ height. The aperture efficiency of the ETPA with the shorting pins is 84.2%. The aperture efficiency is further improved to 94.2% using the SMSH. The measured boresight cross-polarization and side-lobe level are −40 and −29 dB, respectively. The nature of the electricfield and surface current distribution is analyzed, using both the characteristic mode analysis method and high-frequency structure simulator, to understand the role of shorting pin and coaxial feed in converting the non-radiating TM11 mode to the radiating mode. A systematic design process also is presented for a fast design of shorting pin-loaded ETPA on the suitable substrate at a specified frequency.
${{\lambda }}/5$ height. The aperture efficiency of the ETPA with the shorting pins is 84.2%. The aperture efficiency is further improved to 94.2% using the SMSH. The measured boresight cross-polarization and side-lobe level are −40 and −29 dB, respectively. The nature of the electricfield and surface current distribution is analyzed, using both the characteristic mode analysis method and high-frequency structure simulator, to understand the role of shorting pin and coaxial feed in converting the non-radiating TM11 mode to the radiating mode. A systematic design process also is presented for a fast design of shorting pin-loaded ETPA on the suitable substrate at a specified frequency.
Keywords
- Type
- Research Paper
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press in association with The European Microwave Association.





