Let G denote a locally compact metrisable zero dimensional group with left translation invariant metric d. The Lipschitz spaces are defined by
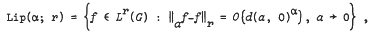
where af: x → f(ax) and α > 0; when r = ∞ the members of Lip(α; r) are taken to be continuous. For a suitable choice of metric it is shown that 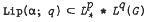 , where 1 ≤ p ≤ 2, α > q−1, p, q are conjugate indices and
, where 1 ≤ p ≤ 2, α > q−1, p, q are conjugate indices and 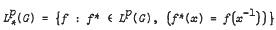 . It is also shown that for G infinite the range of values of α cannot be extended.
. It is also shown that for G infinite the range of values of α cannot be extended.