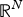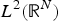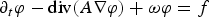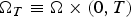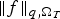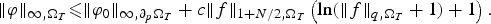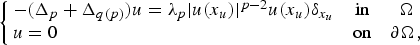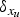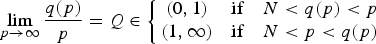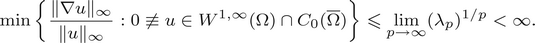Research Article
Finite speed of disturbance for the nonlinear Schrödinger equation
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1405-1419
-
- Article
- Export citation
Pólya S3-extensions of ℚ
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1421-1433
-
- Article
- Export citation
Some generic properties of Schrödinger operators with radial potentials
- Part of:
-
- Published online by Cambridge University Press:
- 15 January 2019, pp. 1435-1451
-
- Article
- Export citation
Triangulations with few vertices of manifolds with non-free fundamental group
- Part of:
-
- Published online by Cambridge University Press:
- 15 January 2019, pp. 1453-1463
-
- Article
- Export citation
Some results on extension of maps and applications
- Part of:
-
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1465-1472
-
- Article
- Export citation
Generalized monotonicity in terms of differential inequalities
- Part of:
-
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1473-1479
-
- Article
- Export citation
Logarithmic upper bounds for weak solutions to a class of parabolic equations
- Part of:
-
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1481-1491
-
- Article
- Export citation
Asymptotic behaviour as p → ∞ of least energy solutions of a (p, q(p))-Laplacian problem
- Part of:
-
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1493-1522
-
- Article
- Export citation
Codimension two spacelike submanifolds of the Lorentz-Minkowski spacetime into the light cone
- Part of:
-
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1523-1553
-
- Article
- Export citation
On critical exponents of a k-Hessian equation in the whole space
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2019, pp. 1555-1575
-
- Article
- Export citation
Optimal growth of harmonic functions frequently hypercyclic for the partial differentiation operator
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2019, pp. 1577-1594
-
- Article
- Export citation
A note on rigidity theorem of λ-hypersurfaces
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2019, pp. 1595-1601
-
- Article
- Export citation
Radial symmetry of non-maximal entire solutions of a bi-harmonic equation with exponential nonlinearity
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2019, pp. 1603-1625
-
- Article
- Export citation
Non-collapsing in homogeneity greater than one via a two-point method for a special case
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2019, pp. 1627-1635
-
- Article
- Export citation
Estimates for the order of Nevanlinna matrices and a Berezanskii-type theorem
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1637-1661
-
- Article
- Export citation
Spectral transitions for Aharonov-Bohm Laplacians on conical layers
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1663-1687
-
- Article
- Export citation
Correction
Corrigendum to: Dirichlet and Neumann boundary conditions for the p-Laplace operator: What is in between?
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1689-1691
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PRM volume 149 issue 6 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 November 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PRM volume 149 issue 6 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 November 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation