Article contents
Some generic properties of Schrödinger operators with radial potentials
Published online by Cambridge University Press: 15 January 2019
Abstract
We consider a class of Schrödinger operators on 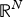 ${\open R}^N$ with radial potentials. Viewing them as self-adjoint operators on the space of radially symmetric functions in
${\open R}^N$ with radial potentials. Viewing them as self-adjoint operators on the space of radially symmetric functions in 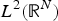 $L^2({\open R}^N)$, we show that the following properties are generic with respect to the potential:
$L^2({\open R}^N)$, we show that the following properties are generic with respect to the potential:
(P1) the eigenvalues below the essential spectrum are nonresonant (i.e., rationally independent) and so are the square roots of the moduli of these eigenvalues;
(P2) the eigenfunctions corresponding to the eigenvalues below the essential spectrum are algebraically independent on any nonempty open set.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 6 , December 2019 , pp. 1435 - 1451
- Copyright
- Copyright © Royal Society of Edinburgh 2019
References
- 1
- Cited by




