Article contents
Logarithmic upper bounds for weak solutions to a class of parabolic equations
Published online by Cambridge University Press: 16 January 2019
Abstract
It is well known that a weak solution φ to the initial boundary value problem for the uniformly parabolic equation 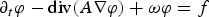 $\partial _t\varphi - {\rm div}(A\nabla \varphi ) +\omega \varphi = f $ in
$\partial _t\varphi - {\rm div}(A\nabla \varphi ) +\omega \varphi = f $ in 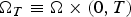 $\Omega _T\equiv \Omega \times (0,T)$ satisfies the uniform estimate
$\Omega _T\equiv \Omega \times (0,T)$ satisfies the uniform estimate
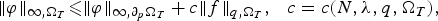 $$\Vert \varphi \Vert_{\infty,\Omega_T}\les \Vert \varphi\Vert_{\infty,\partial_p\Omega_T}+c \Vert f \Vert_{q,\Omega_T}, \ \ \ c=c(N,\lambda, q, \Omega_T), $$
$$\Vert \varphi \Vert_{\infty,\Omega_T}\les \Vert \varphi\Vert_{\infty,\partial_p\Omega_T}+c \Vert f \Vert_{q,\Omega_T}, \ \ \ c=c(N,\lambda, q, \Omega_T), $$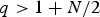 $q \gt 1+{N}/{2}$, where Ω is a bounded domain in
$q \gt 1+{N}/{2}$, where Ω is a bounded domain in 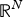 ${\open R}^N$ with Lipschitz boundary, T > 0,
${\open R}^N$ with Lipschitz boundary, T > 0, 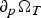 $\partial _p\Omega _T$ is the parabolic boundary of
$\partial _p\Omega _T$ is the parabolic boundary of 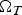 $\Omega _T$,
$\Omega _T$, 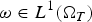 $\omega \in L^1(\Omega _T)$ with
$\omega \in L^1(\Omega _T)$ with 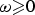 $\omega \ges 0$, and λ is the smallest eigenvalue of the coefficient matrix A. This estimate is sharp in the sense that it generally fails if
$\omega \ges 0$, and λ is the smallest eigenvalue of the coefficient matrix A. This estimate is sharp in the sense that it generally fails if 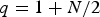 $q=1+{N}/{2}$. In this paper, we show that the linear growth of the upper bound in
$q=1+{N}/{2}$. In this paper, we show that the linear growth of the upper bound in 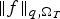 $\Vert f \Vert_{q,\Omega _T}$ can be improved. To be precise, we establish
$\Vert f \Vert_{q,\Omega _T}$ can be improved. To be precise, we establish
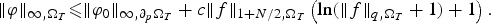 $$ \Vert \varphi \Vert_{\infty,\Omega_T}\les \Vert \varphi_0 \Vert_{\infty,\partial_p\Omega_T}+c \Vert f \Vert_{1+{N}/{2},\Omega_T} \left(\ln(\Vert f \Vert_{q,\Omega_T}+1)+1\right). $$
$$ \Vert \varphi \Vert_{\infty,\Omega_T}\les \Vert \varphi_0 \Vert_{\infty,\partial_p\Omega_T}+c \Vert f \Vert_{1+{N}/{2},\Omega_T} \left(\ln(\Vert f \Vert_{q,\Omega_T}+1)+1\right). $$
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 6 , December 2019 , pp. 1481 - 1491
- Copyright
- Copyright © Royal Society of Edinburgh 2019
References
- 1
- Cited by




