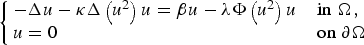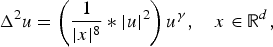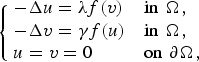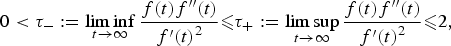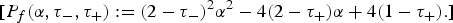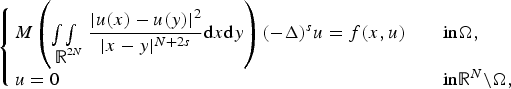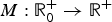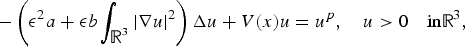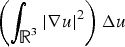Research Article
Space-like hypersurfaces with functionally bounded mean curvature in Lorentzian warped products and generalized Calabi–Bernstein-type problems
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2018, pp. 849-868
-
- Article
- Export citation
A proof of Boca's Theorem
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 869-876
-
- Article
- Export citation
Autonomous and non-autonomous unbounded attractors under perturbations
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 877-903
-
- Article
- Export citation
Mean values of derivatives of L-functions in function fields: III
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 905-913
-
- Article
- Export citation
A quantitative Carleman estimate for second-order elliptic operators
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 915-938
-
- Article
- Export citation
Bifurcation and standing wave solutions for a quasilinear Schrödinger equation
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 939-968
-
- Article
- Export citation
A problem of integer partitions and numerical semigroups
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 969-978
-
- Article
- Export citation
Classification of nonnegative solutions to a bi-harmonic equation with Hartree type nonlinearity
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 979-994
-
- Article
- Export citation
Uniform moment propagation for the Becker--Döring equations
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 995-1015
-
- Article
- Export citation
On the boundary regularity of phase-fields for Willmore's energy
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1017-1035
-
- Article
- Export citation
Regularity of the extremal solutions associated with elliptic systems
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1037-1046
-
- Article
- Export citation
Residually many BV homeomorphisms map a null set onto a set of full measure
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1047-1059
-
- Article
- Export citation
Existence results for Kirchhoff–type superlinear problems involving the fractional Laplacian
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1061-1081
-
- Article
- Export citation
Perturbed Schrödinger lattice systems: existence of homoclinic solutions
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1083-1096
-
- Article
- Export citation
Multi-peak positive solutions to a class of Kirchhoff equations
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1097-1122
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PRM volume 149 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 02 August 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PRM volume 149 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 02 August 2019, pp. b1-b4
-
- Article
-
- You have access
- Export citation




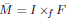 , where
, where