Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-24T02:40:05.518Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence results for Kirchhoff–type superlinear problems involving the fractional Laplacian

Part of: Variational problems in infinite-dimensional spaces Elliptic equations and systems Existence theories Partial differential equations

Published online by Cambridge University Press:  27 December 2018

Zhang Binlin ,
Vicenţiu D. Rădulescu  and
Li Wang
Zhang Binlin
Affiliation:
Department of Mathematics, Heilongjiang Institute of Technology, 150050 Harbin, P. R. China (zhangbinlin2012@163.com)
Vicenţiu D. Rădulescu
Affiliation:
Faculty of Applied Mathematics, AGH University of Science and Technology, al. Mickiewicza 30, 30-059 Kraków, Poland and Institute of Mathematics “Simion Stoilow” of the Romanian Academy, P.O. Box 1-764, 014700 Bucharest, Romania (vicentiu.radulescu@imar.ro)
Li Wang
Affiliation:
College of Science, East China Jiaotong University, 330013 Nanchang, P. R. China (wangli.423@163.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the existence and multiplicity of solutions for Kirchhoff-type superlinear problems involving non-local integro-differential operators. As a particular case, we consider the following Kirchhoff-type fractional Laplace equation:

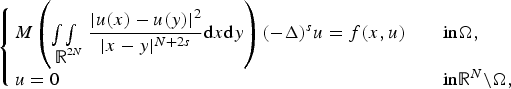$$\matrix{ {\left\{ {\matrix{ {M\left( {\int\!\!\!\int\limits_{{\open R}^{2N}} {\displaystyle{{ \vert u(x)-u(y) \vert ^2} \over { \vert x-y \vert ^{N + 2s}}}} {\rm d}x{\rm d}y} \right){(-\Delta )}^su = f(x,u)\quad } \hfill & {{\rm in }\Omega ,} \hfill \cr {u = 0\quad } \hfill & {{\rm in }{\open R}^N{\rm \setminus }\Omega {\mkern 1mu} ,} \hfill \cr } } \right.} \hfill \cr } $$
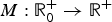where ( − Δ)s is the fractional Laplace operator, s ∈ (0, 1), N > 2s, Ω is an open bounded subset of ℝN with smooth boundary ∂Ω, $M:{\open R}_0^ + \to {\open R}^ + $ is a continuous function satisfying certain assumptions, and f(x, u) is superlinear at infinity. By computing the critical groups at zero and at infinity, we obtain the existence of non-trivial solutions for the above problem via Morse theory. To the best of our knowledge, our results are new in the study of Kirchhoff–type Laplacian problems.

Keywords

Fractional LaplacianKirchhoff–type problemcritical groupsMorse theory

MSC classification

Primary: 35A15: Variational methods
Secondary: 35J91: Semilinear elliptic equations with Laplacian, bi-Laplacian or poly-Laplacian 49J35: Minimax problems 58E05: Abstract critical point theory (Morse theory, Ljusternik-Schnirelman (Lyusternik-Shnirel'man) theory, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 4 , August 2019 , pp. 1061 - 1081
Copyright
Copyright © Royal Society of Edinburgh 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ambrosetti, A. and Rabinowiz, P.. Dual variational methods in critical point theory and applications. J. Funct. Anal. 14 (1973), 349–381.Google Scholar
2Autuori, G., Fiscella, A. and Pucci, P.. Stationary Kirchhoff problems involving a fractional operator and a critical nonlinearity. Nonlinear Anal. 125 (2015), 699–714.Google Scholar
3Bartsch, T. and Li, S.. Critical point theory for asymptotically quadratic functionals and applications to problems with resonance. Nonlinear Anal. 28 (1997), 419–441.Google Scholar
4Binlin, Z., Molica Bisci, G. and Servadei, R.. Superlinear nonlocal fractional problems with infinitely many solutions. Nonlinearity 28 (2015), 2247–2264.Google Scholar
5Binlin, Z., Molica Bisci, G. and Xiang, M.. Multiplicity results for nonlocal fractional p–Kirchhoff equations via Morse theory. Topol. Methods Nonlinear Anal. 49 (2017), 445–461.Google Scholar
6Bucur, C. and Valdinoci, E.. Nonlocal diffusion and applications, volume 20 of Lecture Notes of the Unione Matematica Italiana. Springer, [Cham]; Unione Matematica Italiana, Bologna, 2016. xii+155 pp. ISBN: 978-3-319-28738-6; 978-3-319-28739-3.Google Scholar
7Cabré, X. and Tan, J.. Positive solutions of nonlinear problems involving the square root of the Laplacian. Adv. Math. 224 (2010), 2052–2093.Google Scholar
8Chang, K.. Infinite dimensional Morse theory and multiple solution problems (Boston: Birkhäuser, 1993).Google Scholar
9Chen, S. and Liu, S.. Standing waves for 4–superlinear Schrödinger–Kirchhoff equations. Math. Methods. Appl. Sci. 38 (2015), 2185–2193.Google Scholar
10Chen, Y. and Su, J.. Resonant problems for fractional Laplacian. Comm. Pure Appl. Anal. 16 (2017), 163–187.Google Scholar
11Di Nezza, E., Palatucci, G. and Valdinoci, E.. Hitchhiker's guide to the fractional Sobolev spaces. Bull. Sci. Math. 136 (2012), 521–573.Google Scholar
12Dinca, G., Jebelean, P. and Mawhin, J.. Variational and topological methods for Dirichlet problems with p–Laplacian. Portugal. Math. 58 (2001), 339–378.Google Scholar
13Fang, F. and Liu, S.. Nontrivial solutions of superlinear p–Laplacian equations. J. Math. Anal. Appl. 351 (2009), 138–146.Google Scholar
14Ferrara, M., Molica Bisci, G. and Zhang, B.. Existence of weak solutions for non-local fractional problems via Morse theory. Discrete Contin. Dyn. Syst. Ser. B 9 (2014), 2483–2499.Google Scholar
15Fiscella, A. and Valdinoci, E.. A critical Kirchhoff type problem involving a nonlocal operator. Nonlinear Anal. 94 (2014), 156–170.Google Scholar
16Fiscella, A., Servadei, R. and Valdinoci, E.. Density properties for fractional Sobolev spaces. Ann. Acad. Sci. Fenn. Math. 40 (2015), 235–253.Google Scholar
17Iannizzotto, A., Liu, S., Perera, K., Squassina, M.. Existence results for fractional p–Laplacian problems via Morse theory, Adv. Calc. Var. 9 (2016), 101–125.Google Scholar
18Jeanjean, L.. On the existence of bounded Palais-Smale sequences and application to a Landesman-Lazer type problem set on ℝN. Proc. Roy. Soc. Edinburgh A 129 (1999), 787–809.Google Scholar
19Lions, J.-L.. On some questions in boundary value problems of mathematical physics, in: Contemporary Developments in Continuum Mechanics and Partial Differential Equations, Proc. Internat. Sympos., Inst. Mat. Univ. Fed. Rio de Janeiro, Rio de Janeiro, 1977, North–Holland Math. Stud., North–Holland, Amsterdam 30 (1978), 284–346.Google Scholar
20Liu, S.. Existence of solutions to a superlinear p–Laplacian equation. Electron. J. Differ. Equ. 66 (2001), 1–6.Google Scholar
21Liu, S.. On ground states of superlinear p–Laplacian equations in ℝN. J. Math. Anal. Appl. 361 (2010), 48–58.Google Scholar
22Liu, J. and Su, J.. Remarks on multiple nontrivial solutions for quasi–linear resonant problems. J. Math. Anal. Appl. 258 (2001), 209–222.Google Scholar
23Liu, Q. and Su, J.. Existence and multiplicity results for Dirichlet problems with p-Laplacian. J. Math. Anal. Appl. 281 (2003), 587–601.Google Scholar
24Mingqi, X., Molica Bisci, G., Tian, G. and Zhang, B.. Infinitely many solutions for the stationary Kirchhoff problems involving the fractional p–Laplacian. Nonlinearity 29 (2016), 357–374.Google Scholar
25Molica Bisci, G. and Rădulescu, V.. Ground state solutions of scalar field fractional Schrödinger equations. Calc. Var. Partial Differ. Equ. 54 (2015), 2985–3008.Google Scholar
26Molica Bisci, G., Rădulescu, V. and Servadei, R.. Variational Methods for Nonlocal Fractional Problems, Encyclopedia of Mathematics and its Applications, 162 (Cambridge: Cambridge University Press, 2016).Google Scholar
27Perera, K. and Zhang, Z.. Nontrivial solutions of Kirchhoff-type problems via the Yang index. J. Differ. Equ. 221 (2006), 246–255.Google Scholar
28Pucci, P. and Saldi, S.. Critical stationary Kirchhoff equations in ℝN involving nonlocal operators. Rev. Mat. Iberoam. 32 (2016), 1–22.Google Scholar
29Pucci, P., Xiang, M. and Zhang, B.. Multiple solutions for nonhomogenous Schrödinger-Kirchhoff type equations involving the fractional p–Laplacian in ℝN. Calc. Var. Partial Differ. Equ. 54 (2015), 2785–2806.Google Scholar
30Pucci, P., Xiang, M. and Zhang, B.. Existence and multiplicity of entire solutions for fractional p–Kirchhoff equations. Adv. Nonlinear Anal. 5 (2016), 27–55.Google Scholar
31Rădulescu, V. and Zhang, B.. Morse theory and local linking for a nonlinear degenerate problem arising in the theory of electrorheological fluids. Nonlinear Anal. Real World Appl. 17 (2014), 311–321.Google Scholar
32Servadei, R. and Valdinoci, E.. Mountain Pass solutions for non-local elliptic operators. J. Math. Anal. Appl. 389 (2012), 887–898.Google Scholar
33Servadei, R. and Valdinoci, E.. Lewy–Stampacchia type estimates for variational inequalities driven by (non)local operators. Rev. Mat. Iberoam. 29 (2013), 1091–1126.Google Scholar
34Servadei, R. and Valdinoci, E.. Variational methods for non-local operators of elliptic type. Discrete Contin. Dyn. Syst. 33 (2013), 2105–2137.Google Scholar
35Servadei, R. and Valdinoci, E.. On the spectrum of two different fractional operators. Proc. Roy. Soc. Edinburgh Sect. A 144 (2014), 831–855.Google Scholar
36Wang, L. and Zhang, B.. Infinitely many solutions for Schrödinger-Kirchhoff type equations involving the fractional p-Laplacian and critical exponent. Electron. J. Differ. Equ. (2016), No. 339, 18 pp.Google Scholar
37Xiang, M., Zhang, B. and Ferrara, M.. Existence of solutions for Kirchhoff type problem involving the non–local fractional p–Laplacian. J. Math. Anal. Appl. 424 (2015), 1021–1041.Google Scholar
38Xiang, M., Zhang, B. and Rădulescu, V.. Multiplicity of solutions for a class of quasilinear Kirchhoff system involving the fractional p–Laplacian. Nonlinearity 29 (2016), 3186–3205.Google Scholar
39Xiang, M., Zhang, B. and Rădulescu, V.. Existence of solutions for perturbed fractional p–Laplacian equations. J. Differ. Equ. 260 (2016), 1392–1413.Google Scholar
40Zhang, X., Zhang, B. and Repovš, D.. Existence and symmetry of solutions for critical fractional Schrödinger equations with bounded potentials. Nonlinear Anal. 142 (2016), 48–68.Google Scholar