Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dai, Wei
and
Liu, Zhao
2019.
Classification of nonnegative solutions to static Schrödinger–Hartree and Schrödinger–Maxwell equations with combined nonlinearities.
Calculus of Variations and Partial Differential Equations,
Vol. 58,
Issue. 4,
Dai, Wei
and
Qin, Guolin
2020.
Liouville type theorems for elliptic equations with Dirichlet conditions in exterior domains.
Journal of Differential Equations,
Vol. 269,
Issue. 9,
p.
7231.
Dai, Wei
and
Qin, Guolin
2020.
Liouville theorem for poly-harmonic functions on $${{\mathbb {R}}}^{n}_{+}$$.
Archiv der Mathematik,
Vol. 115,
Issue. 3,
p.
317.
Dai, Wei
and
Qin, Guolin
2020.
Liouville type theorems for Hardy–Hénon equations with concave nonlinearities.
Mathematische Nachrichten,
Vol. 293,
Issue. 6,
p.
1084.
Dai, Wei
and
Qin, Guolin
2021.
Maximum principles and the method of moving planes for the uniformly elliptic nonlocal Bellman operator and applications.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 200,
Issue. 3,
p.
1085.
Saanouni, Tarek
2021.
Energy scattering for radial focusing inhomogeneous bi-harmonic Schrödinger equations.
Calculus of Variations and Partial Differential Equations,
Vol. 60,
Issue. 3,
Dai, Wei
Qin, Guolin
and
Wu, Dan
2021.
Direct Methods for Pseudo-relativistic Schrödinger Operators.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 6,
p.
5555.
Li, Yunting
Liu, Yaqiong
and
Yi, Yunhui
2021.
Classification of nonnegative solutions to static Schrödinger–Hartree–Maxwell system involving the fractional Laplacian.
Boundary Value Problems,
Vol. 2021,
Issue. 1,
Dai, Wei
Liu, Zhao
and
Qin, Guolin
2021.
Classification of Nonnegative Solutions to Static Schrödinger--Hartree--Maxwell Type Equations.
SIAM Journal on Mathematical Analysis,
Vol. 53,
Issue. 2,
p.
1379.
Liu, Yaqiong
Li, Yunting
Liao, Qiuping
and
Yi, Yunhui
2021.
Classification of nonnegative solutions to fractional Schrödinger-Hatree-Maxwell type system.
AIMS Mathematics,
Vol. 6,
Issue. 12,
p.
13665.
Dai, Wei
and
Peng, Shaolong
2021.
Liouville theorems for nonnegative solutions to static weighted Schrödinger–Hartree–Maxwell type equations with combined nonlinearities.
Analysis and Mathematical Physics,
Vol. 11,
Issue. 2,
Peng, Shaolong
2021.
Liouville theorems for fractional and higher-order Hénon–Hardy systems on ℝn.
Complex Variables and Elliptic Equations,
Vol. 66,
Issue. 11,
p.
1839.
Dai, Wei
Peng, Shaolong
and
Qin, Guolin
2022.
Liouville type theorems, a priori estimates and existence of solutions for sub-critical order Lane—Emden—Hardy equations.
Journal d'Analyse Mathématique,
Vol. 146,
Issue. 2,
p.
673.
Dai, Wei
and
Fu, Jingze
2022.
On properties of positive solutions to nonlinear tri-harmonic and bi-harmonic equations with negative exponents.
Bulletin of Mathematical Sciences,
Vol. 12,
Issue. 03,
Peng, Shaolong
2022.
Existence and Liouville theorems for coupled fractional elliptic system with Stein–Weiss type convolution parts.
Mathematische Zeitschrift,
Vol. 302,
Issue. 3,
p.
1593.
Dai, Wei
Liu, Zhao
and
Wang, Pengyan
2022.
Monotonicity and symmetry of positive solutions to fractional p-Laplacian equation.
Communications in Contemporary Mathematics,
Vol. 24,
Issue. 06,
Peng, Shaolong
2023.
Classification of nonnegative solutions to Schrödinger equation with logarithmic nonlinearity.
Journal of Fixed Point Theory and Applications,
Vol. 25,
Issue. 1,
Chen, Wenxiong
Dai, Wei
and
Qin, Guolin
2023.
Liouville type theorems, a priori estimates and existence of solutions for critical and super-critical order Hardy–Hénon type equations in $$\mathbb {R}^{n}$$.
Mathematische Zeitschrift,
Vol. 303,
Issue. 4,
Guo, Yuxia
and
Peng, Shaolong
2023.
Liouville-type theorems for higher-order Lane–Emden system in exterior domains.
Communications in Contemporary Mathematics,
Vol. 25,
Issue. 05,
Dai, Wei
2023.
Liouville type theorems for poly-harmonic Dirichlet problems of Hénon-Hardy type equations on a half space or a ball.
Collectanea Mathematica,
Vol. 74,
Issue. 3,
p.
729.
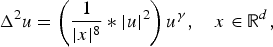 $$\Delta ^2u = \left( {\displaystyle{1 \over { \vert x \vert ^8}}* \vert u \vert ^2} \right)u^\gamma ,\quad x\in {\open R}^d,$$
$$\Delta ^2u = \left( {\displaystyle{1 \over { \vert x \vert ^8}}* \vert u \vert ^2} \right)u^\gamma ,\quad x\in {\open R}^d,$$

