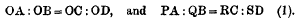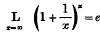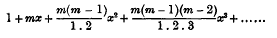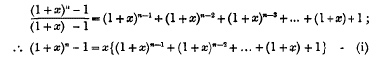Office-Bearers
Office-Bearers
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 1
-
- Article
-
- You have access
- Export citation
Presents to the Library
The following Presents to the Library have been received, for which the Society tenders its grateful thanks
-
- Published online by Cambridge University Press:
- 04 February 2019, pp. 7-8
-
- Article
-
- You have access
- Export citation
Research Article
Geometrical Theory of the Hyperbolic Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 2-8
-
- Article
-
- You have access
- Export citation
Vorlesungen über Geschichte der Mathematik, von Moritz Cantor. Dritter (Schluss) Band
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 9-32
-
- Article
-
- You have access
- Export citation
Note on the Inequality Theorems that lead up to the Exponential Limit
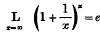
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 33-37
-
- Article
-
- You have access
- Export citation
Against Euler's Proof of the Binomial Theorem for Negative and Fractional Exponents
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 38-41
-
- Article
-
- You have access
- Export citation
A Proof of the Binomial Theorem when the Exponent is a Positive Integer
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 42
-
- Article
-
- You have access
- Export citation
Other
On a Problem of Lewis Carroll's
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 68
-
- Article
-
- You have access
- Export citation
Research Article
On the Eight Queens Problem
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 43-68
-
- Article
-
- You have access
- Export citation
Other
On Wireless Telegraphy and High Potential Currents
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 69
-
- Article
-
- You have access
- Export citation
Discussion on “The Treatment of Proportion in Elementary Mathematics”
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 69
-
- Article
-
- You have access
- Export citation
Research Article
Centrobaric Spherical Surface Distribution
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 68-69
-
- Article
-
- You have access
- Export citation
Systems of Circles analogous to Tucker Circles*
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 70-99
-
- Article
-
- You have access
- Export citation
Systems of Conics connected with the Triangle
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 99-107
-
- Article
-
- You have access
- Export citation
Other
“La Perspective d'une Conique est une Conique.” Démonstration Élémentaire
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 112
-
- Article
-
- You have access
- Export citation
Research Article
Systems of Spheres connected with the Tetrahedron
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 108-112
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 17 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back matter
PEM volume 17 Back matter and figures
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. b1-b17
-
- Article
-
- You have access
- Export citation