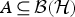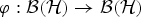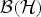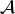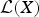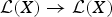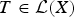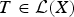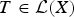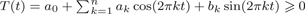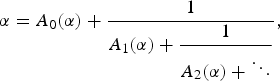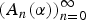Research Article
On the Range Inclusion for Normal Derivations on C*-algebras
- Part of:
-
- Published online by Cambridge University Press:
- 22 February 2017, pp. 1-11
-
- Article
- Export citation
An intrinsic definition of the Rees algebra of a module
- Part of:
-
- Published online by Cambridge University Press:
- 22 February 2017, pp. 13-30
-
- Article
- Export citation
Numerical Ranges in II1 Factors
- Part of:
-
- Published online by Cambridge University Press:
- 16 March 2017, pp. 31-55
-
- Article
- Export citation
A Convenient Notion of Compact Set for Generalized Functions
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2017, pp. 57-92
-
- Article
- Export citation
Convergence of a Time Discretization for a Nonlinear Second-Order Inclusion
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2017, pp. 93-120
-
- Article
- Export citation
Segal's Spectral Sequence in Twisted Equivariant K-theory for Proper and Discrete Actions
- Part of:
-
- Published online by Cambridge University Press:
- 23 January 2018, pp. 121-150
-
- Article
- Export citation
Local Fractal Interpolation on Unbounded Domains
- Part of:
-
- Published online by Cambridge University Press:
- 23 January 2018, pp. 151-167
-
- Article
- Export citation
Linear Surjective Maps Preserving at Least One Element from the Local Spectrum
- Part of:
-
- Published online by Cambridge University Press:
- 23 January 2018, pp. 169-175
-
- Article
- Export citation
Erratum
Algebraic Cycles on Quadric Sections of Cubics in ℙ4 Under the Action of Symplectomorphisms – Erratum
-
- Published online by Cambridge University Press:
- 23 January 2018, p. 177
-
- Article
-
- You have access
- Export citation
Research Article
The Point Value Maximization Problem for Positive Definite Functions Supported in a Given Subset of a Locally Compact Group
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2018, pp. 179-200
-
- Article
- Export citation
An Elliptic PDE with Convex Solutions
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2018, pp. 201-214
-
- Article
- Export citation
Visualizing Automorphisms of Graph Algebras
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2018, pp. 215-249
-
- Article
- Export citation
Maximal Ideals in Some Spaces of Bounded Linear Operators
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2018, pp. 251-264
-
- Article
- Export citation
Leibniz Rule on Higher Pages of Unstable Spectral Sequences
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2018, pp. 265-282
-
- Article
- Export citation
On the Quantitative Metric Theory of Continued Fractions in Positive Characteristic
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2018, pp. 283-293
-
- Article
-
- You have access
- Open access
- Export citation
On the Square Subgroup of a Mixed SI-Group
- Part of:
-
- Published online by Cambridge University Press:
- 15 February 2018, pp. 295-304
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PEM series 2 volume 61 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 15 March 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PEM series 2 volume 61 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 15 March 2018, pp. b1-b2
-
- Article
-
- You have access
- Export citation