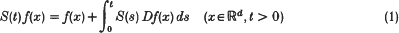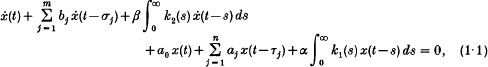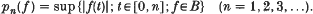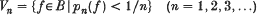Research Article
Presentations for Conway's group Co1
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-3
-
- Article
- Export citation
Small independent zeros of quadratic forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 5-16
-
- Article
- Export citation
The maximal subgroups of Fi22
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 17-23
-
- Article
- Export citation
Generalized triangle groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-31
-
- Article
- Export citation
The classification of finite simple Moufang loops
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 33-47
-
- Article
- Export citation
Reduction numbers for ideals of higher analytic spread
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-57
-
- Article
- Export citation
Birational pairs according to S. Iitaka
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 59-69
-
- Article
- Export citation
Unstable Adams operations on classifying spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 71-75
-
- Article
- Export citation
Hermitian character and the first problem for R. H. Fox for links
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 77-86
-
- Article
- Export citation
Non-simple universal knots
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 87-95
-
- Article
- Export citation
Only integral Dehn surgeries can yield reducible manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 97-101
-
- Article
- Export citation
Low-dimensional concordances, Whitney towers and isotopies
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-119
-
- Article
- Export citation
Alternating projections between a strip and a halfplane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 121-129
-
- Article
- Export citation
A note on maximal operators of Hardy–Littlewood type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 131-134
-
- Article
- Export citation
A Tauberian theorem for Borel summability
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-138
-
- Article
- Export citation
Semigroups and diffusion processes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 139-148
-
- Article
- Export citation
A simple stability criterion for a linear system of neutral integro-differential equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 149-162
-
- Article
- Export citation
On heat capacity and parabolic measure
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 163-172
-
- Article
- Export citation
A note on Hamiltonian structure
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 173-189
-
- Article
- Export citation
Corrigendum
Corrigenda
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 191
-
- Article
-
- You have access
- Export citation



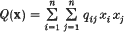
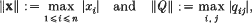

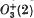 ) should read
) should read 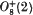 .) More precisely, we prove
.) More precisely, we prove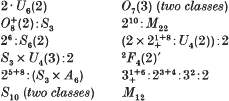
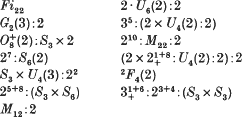
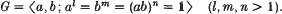

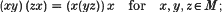
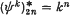 . Id
. Id defined by
defined by 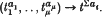 . Then the Z〈
. Then the Z〈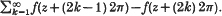 . We show that for every
. We show that for every