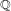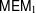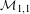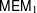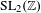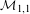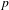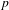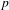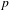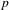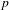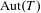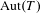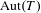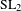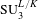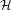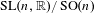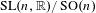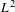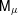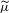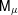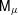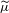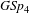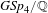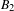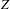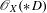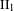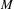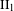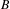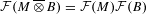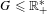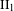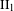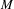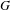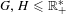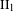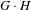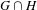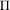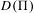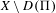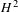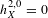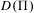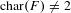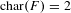Research Article
UNIVERSAL MIXED ELLIPTIC MOTIVES
- Part of:
-
- Published online by Cambridge University Press:
- 30 April 2018, pp. 663-766
-
- Article
- Export citation
UNRAMIFIEDNESS OF GALOIS REPRESENTATIONS ATTACHED TO HILBERT MODULAR FORMS MOD
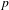 $p$ OF WEIGHT 1
$p$ OF WEIGHT 1
- Part of:
-
- Published online by Cambridge University Press:
- 23 April 2018, pp. 281-306
-
- Article
- Export citation
CHABAUTY LIMITS OF ALGEBRAIC GROUPS ACTING ON TREES THE QUASI-SPLIT CASE
- Part of:
-
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1031-1091
-
- Article
- Export citation
SUR L’ÉTUDE DE L’ENTROPIE DES APPLICATIONS MÉROMORPHES
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 1-19
-
- Article
- Export citation
SPECTRAL ANALYSIS OF MORSE–SMALE FLOWS I: CONSTRUCTION OF THE ANISOTROPIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 13 November 2018, pp. 1409-1465
-
- Article
- Export citation
ANALOGUES OF CENTRALIZER SUBALGEBRAS FOR FIAT 2-CATEGORIES AND THEIR 2-REPRESENTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1793-1829
-
- Article
- Export citation
CHABAUTY LIMITS OF SIMPLE GROUPS ACTING ON TREES
- Part of:
-
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1093-1120
-
- Article
- Export citation
ZERO-LOCI OF BRAUER GROUP ELEMENTS ON SEMI-SIMPLE ALGEBRAIC GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1467-1507
-
- Article
- Export citation
UNIVERSAL COVERS OF COMMUTATIVE FINITE MORLEY RANK GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 26 April 2018, pp. 767-799
-
- Article
- Export citation
LARGE-SCALE SUBLINEARLY LIPSCHITZ GEOMETRY OF HYPERBOLIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1831-1876
-
- Article
- Export citation
APPROXIMATION OF
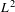 $L^{2}$-ANALYTIC TORSION FOR ARITHMETIC QUOTIENTS OF THE SYMMETRIC SPACE
$L^{2}$-ANALYTIC TORSION FOR ARITHMETIC QUOTIENTS OF THE SYMMETRIC SPACE 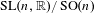 $\operatorname{SL}(n,\mathbb{R})/\operatorname{SO}(n)$
$\operatorname{SL}(n,\mathbb{R})/\operatorname{SO}(n)$
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2018, pp. 307-350
-
- Article
- Export citation
GENERALIZED THOM SPECTRA AND THEIR TOPOLOGICAL HOCHSCHILD HOMOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 21-64
-
- Article
- Export citation
RANDOM SPARSE SAMPLING IN A GIBBS WEIGHTED TREE AND PHASE TRANSITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 09 May 2018, pp. 65-116
-
- Article
- Export citation
AN EQUIDISTRIBUTION THEOREM FOR HOLOMORPHIC SIEGEL MODULAR FORMS FOR
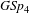 $\mathit{GSp}_{4}$ AND ITS APPLICATIONS
$\mathit{GSp}_{4}$ AND ITS APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 22 February 2018, pp. 351-419
-
- Article
- Export citation
LOCAL VANISHING AND HODGE FILTRATION FOR RATIONAL SINGULARITIES
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2018, pp. 801-819
-
- Article
- Export citation
ON FUNDAMENTAL GROUPS OF TENSOR PRODUCT
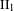 $\text{II}_{1}$ FACTORS
$\text{II}_{1}$ FACTORS
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2018, pp. 1121-1139
-
- Article
- Export citation
A BOGOMOLOV UNOBSTRUCTEDNESS THEOREM FOR LOG-SYMPLECTIC MANIFOLDS IN GENERAL POSITION
- Part of:
-
- Published online by Cambridge University Press:
- 09 November 2018, pp. 1509-1519
-
- Article
- Export citation
ANALYTIC HYPOELLIPTICITY FOR SUMS OF SQUARES IN THE PRESENCE OF SYMPLECTIC NON TREVES STRATA
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1877-1888
-
- Article
- Export citation
A BOUND FOR THE INDEX OF A QUADRATIC FORM AFTER SCALAR EXTENSION TO THE FUNCTION FIELD OF A QUADRIC
- Part of:
-
- Published online by Cambridge University Press:
- 16 April 2018, pp. 421-450
-
- Article
- Export citation
DEGENERATION OF ENDOMORPHISMS OF THE COMPLEX PROJECTIVE SPACE IN THE HYBRID SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 31 August 2018, pp. 1141-1183
-
- Article
- Export citation