Article contents
ZERO-LOCI OF BRAUER GROUP ELEMENTS ON SEMI-SIMPLE ALGEBRAIC GROUPS
Published online by Cambridge University Press: 29 November 2018
Abstract
We consider the problem of counting the number of rational points of bounded height in the zero-loci of Brauer group elements on semi-simple algebraic groups over number fields. We obtain asymptotic formulae for the counting problem for wonderful compactifications using the spectral theory of automorphic forms. Applications include asymptotic formulae for the number of matrices over 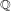 $\mathbb{Q}$ whose determinant is a sum of two squares. These results provide a positive answer to some cases of a question of Serre concerning such counting problems.
$\mathbb{Q}$ whose determinant is a sum of two squares. These results provide a positive answer to some cases of a question of Serre concerning such counting problems.
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 5 , September 2020 , pp. 1467 - 1507
- Copyright
- © Cambridge University Press 2018
References
- 4
- Cited by



