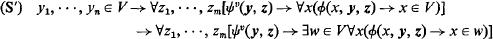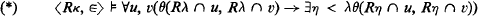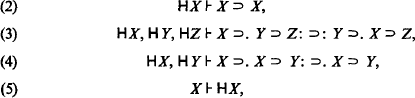Research Article
Countable initial segments of the degrees of unsolvability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 289-300
-
- Article
- Export citation
Modal reduction principles
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 301-312
-
- Article
- Export citation
On finite lattices of degrees of constructibility of reals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 313-322
-
- Article
- Export citation
A completeness theorem for Zermelo-Fraenkel set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 323-327
-
- Article
- Export citation
Derived rules of inference related to the continuity of effective operations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 328-336
-
- Article
- Export citation
An interpretation of “finite” modal first-order languages in classical second-order languages
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 337-340
-
- Article
- Export citation
Krom formulas with one dyadic predicate letter1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 341-362
-
- Article
- Export citation
Uniformly defined descending sequences of degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 363-367
-
- Article
- Export citation
Noncharacterizability of the syntax set
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 368-372
-
- Article
- Export citation
λ-scales, κ-Souslin sets and a new definition of analytic sets1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 373-378
-
- Article
- Export citation
Large and small existentially closed structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 379-390
-
- Article
- Export citation
Projective planes of infinite but isolic order
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 391-404
-
- Article
- Export citation
Congruence relations, filters, ideals, and definability in lattices of α-recursively enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 405-418
-
- Article
- Export citation
Types of simple α-recursively enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 419-426
-
- Article
- Export citation
Equivalence of some definitions of recursion in a higher type object1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 427-435
-
- Article
- Export citation
Modal formulas are either elementary or not ΣΔ-elementary
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 436-438
-
- Article
- Export citation
Normal functions and constructive ordinal notations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 439-459
-
- Article
- Export citation
The decision problem for standard classes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 460-464
-
- Article
- Export citation
Relative consistency of an extension of Ackermann's set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 465-466
-
- Article
- Export citation
The inconsistency of
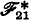
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 467-468
-
- Article
- Export citation



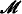
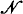 of natural numbers and
of natural numbers and 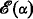 (
(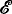 (α) denote the lattice of α-r.e. sets, ordered by set inclusion. An α-r.e. set
(α) denote the lattice of α-r.e. sets, ordered by set inclusion. An α-r.e. set 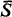 (the complement of
(the complement of