Research Article
Boolean algebras, Stone spaces, and the iterated Turing jump
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1121-1138
-
- Article
- Export citation
On first-order theories with provability operator
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1139-1153
-
- Article
- Export citation
A modified sentence unprovable in PA
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1154-1157
-
- Article
- Export citation
The consistency strength of an infinitary Ramsey property
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1158-1195
-
- Article
- Export citation
Possible behaviours for the Mitchell ordering II
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1196-1209
-
- Article
- Export citation
Strictly primitive recursive realizability, I
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1210-1227
-
- Article
- Export citation
The critical number of a variable in a function
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1228-1244
-
- Article
- Export citation
A partial model of NF with E
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1245-1253
-
- Article
- Export citation
Hereditary undecidability of some theories of finite structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1254-1262
-
- Article
- Export citation
Subformula property in many-valued modal logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1263-1273
-
- Article
- Export citation
Grzegorcyk's hierarchy and IepΣ1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1274-1284
-
- Article
- Export citation
On the number of models of uncountable theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1285-1300
-
- Article
- Export citation
Effective versions of Ramsey's Theorem: Avoiding the cone above 0′
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1301-1325
-
- Article
- Export citation
Initial segments of the lattice of ideals of r.e. degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1326-1350
-
- Article
- Export citation
Scott heights of abelian groups
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1351-1359
-
- Article
- Export citation
Embedding lattices into the wtt-degrees below 0′
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1360-1382
-
- Article
- Export citation
Mixed systems
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1383-1399
-
- Article
- Export citation
Definability of types, and pairs of O-minimal structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1400-1409
-
- Article
- Export citation
On countable fractions from an elementary class
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1410-1413
-
- Article
- Export citation
On the incompleteness theorems
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1414-1419
-
- Article
- Export citation



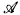 is a countable structure with finite signature, and
is a countable structure with finite signature, and 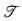 ) is true but not provable in the theory
) is true but not provable in the theory 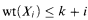
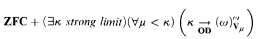
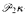 -hypermeasurable and
-hypermeasurable and 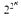 >
> 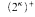 .
.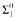 formulae is proved. A dual concept of falsifiability is proposed and an analogous soundness result is established for a further restricted fragment of HA.
formulae is proved. A dual concept of falsifiability is proposed and an analogous soundness result is established for a further restricted fragment of HA.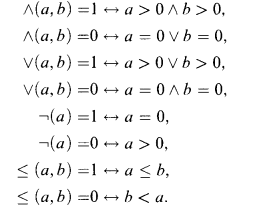
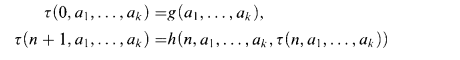
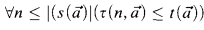 ; and
; and 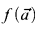 is defined by
is defined by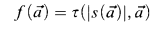
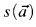 and
and 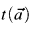 are terms in
are terms in 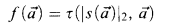
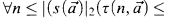
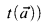 .
.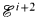 for
for 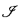 (the lattice of ideals of r.e. degrees) are relevant for the investigation of decidability of (fragments of) the theory of
(the lattice of ideals of r.e. degrees) are relevant for the investigation of decidability of (fragments of) the theory of  , +, 1), where, as usual,
, +, 1), where, as usual, 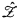 and a torsion-free divisible group, it is easy to see that any such model must be ≡
and a torsion-free divisible group, it is easy to see that any such model must be ≡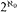 and so must have Scott height below
and so must have Scott height below 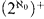 .
.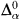 function, where
function, where 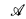 , under suitable assumptions, if
, under suitable assumptions, if  . There is no difficulty in generalizing this to make each of infinitely many relations not
. There is no difficulty in generalizing this to make each of infinitely many relations not 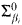 for distinct β
for distinct β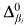 If
If 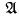 and any formula
and any formula