Research Article
Venn-type diagrams for arguments of n terms
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 113-118
-
- Article
- Export citation
Comments on a variant form of natural deduction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 119-121
-
- Article
- Export citation
Analytic natural deduction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 123-139
-
- Article
- Export citation
Interpretations of Kleene's metamathematical predicate Γ ∣ a in intuitionistic arithmetic1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 140-154
-
- Article
- Export citation
Functionals defined by transfinite recursion
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 155-174
-
- Article
- Export citation
The substitution method
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 175-192
-
- Article
- Export citation
Extensions of the constructive ordinals1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 193-211
-
- Article
- Export citation
Limit ultraproducts
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 212-234
-
- Article
- Export citation
Reviews
Evert W. Beth. Formal methods. An introduction to symbolic logic and to the study of effective operations in arithmetic and logic. Synthese library. D. Reidel Publishing Company, Dordrecht, Holland, and Gordon and Breach, New York, 1962, XIV + 170 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 235-236
-
- Article
- Export citation
Alfred Tarski. Introduction à la logique. French translation of XII 61 by Jacques A. Tremblay. Collection de logique mathématique, série A no. 16. Gauthier-Villars, Paris, and E. Nauwelaerts, Louvain, 1960, XV + 224 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 236-237
-
- Article
- Export citation
Jan Łukasiewicz. Elements of mathematical logic. English translation of 1866 by Olgierd Wojtasiewicz. The Macmillan Company, New York1964, xi + 124 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 237
-
- Article
- Export citation
Alfred North Whitehead and Bertrand Russell. Principia mathematica to *56. A reprint of 1941 as far as *56, including 1944, 1945, 1947. Cambridge University Press, London and New York1962, xlvi + 410 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 237-238
-
- Article
- Export citation
Francesco Barone. La terapia semantica. Il pensiero americano contemporaneo, Filosofia, Epistemologia, Logica, edited by Ferruccio Rossi-Landi, Edizioni di Comunita, Milan1958, pp. 3–24.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 238
-
- Article
- Export citation
Ferruccio Rossi-Landi. Universo del discorso e lingua ideale in filosofia. Il pensiero americano contemporaneo, Filosofia, Epistemologia, Logica, edited by Ferruccio Rossi-Landi, Edizioni di Comunità, Milan1958, pp. 131–182.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 238-239
-
- Article
- Export citation
Uberto Scarpelli. I fondamenti e il metodo della analisi del linguaggio. Il pensiero americano contemporaneo, Filosofia, Epistemologia, Logica, edited by Ferruccio Rossi-Landi, Edizioni di Comunità, Milan1958, pp. 183–204.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 239
-
- Article
- Export citation
Giuseppe Vaccarino. L'implicazione stretta e la logica delle modalità. Il pensiero americano contemporaneo, Filosofia, Epistemologia, Logica, edited by Ferruccio Rossi-Landi, Edizioni di Comunita, Milan1958, pp. 235–270.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 239-240
-
- Article
- Export citation
T. J. Smiley. Entailment and deducibility. Proceedings of the Aristotelian Society, n.s. vol. 59 (1959), pp. 233–254.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 240-241
-
- Article
- Export citation
Leo Apostel. Game theory and the interpretation of deontic logic. Logique et analyse, n.s. vol. 3 (1960), pp. 70–90.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 242
-
- Article
- Export citation
Ward Waddell Jr. Structure of laws as represented by symbolic methods. Published by the author, 495 Fernando St., San Diego, California, 1961, 99 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 242-243
-
- Article
- Export citation
John A. Carpenter, Omar K. Moore, Charles R. Snyder, and Edith S. Lisansky. Alcohol and higher-order problem solving. Quarterly journal of studies on alcohol (New Haven), vol. 22 (1961), pp. 183–222.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 243
-
- Article
- Export citation



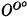 , … and the corresponding ordinals
, … and the corresponding ordinals 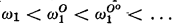 are obtained. A second possibility is to define (constructive) higher number classes in which partial recursive functions are used at limit ordinals to provide an “accessibility” mapping from a previously defined number class. The relationship between the ordinals obtained by the two methods of extension has been an open problem. Methods developed in this article are used to show that the two ways of extending the constructive ordinals are equivalent, provided the sets of notations for the higher number classes satisfy certain natural conditions. Equivalence is obtained, not only with respect to ordinals, but also with respect to the forms of the sets of notations for the higher number classes. Specifically, the fundamental fact that the sets of notations for the constructive ordinals are complete Π
are obtained. A second possibility is to define (constructive) higher number classes in which partial recursive functions are used at limit ordinals to provide an “accessibility” mapping from a previously defined number class. The relationship between the ordinals obtained by the two methods of extension has been an open problem. Methods developed in this article are used to show that the two ways of extending the constructive ordinals are equivalent, provided the sets of notations for the higher number classes satisfy certain natural conditions. Equivalence is obtained, not only with respect to ordinals, but also with respect to the forms of the sets of notations for the higher number classes. Specifically, the fundamental fact that the sets of notations for the constructive ordinals are complete Π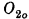 of notations for their third number class is recursively isomorphic to
of notations for their third number class is recursively isomorphic to 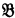 is isomorphic to a limit ultrapower of
is isomorphic to a limit ultrapower of  if and only if every PC
if and only if every PC