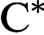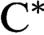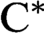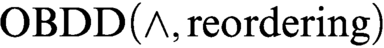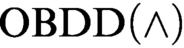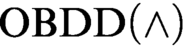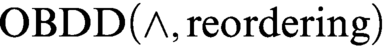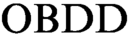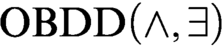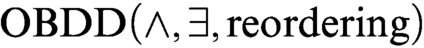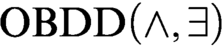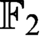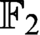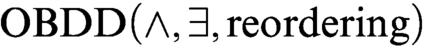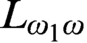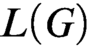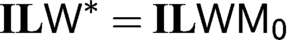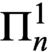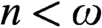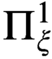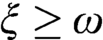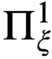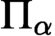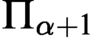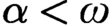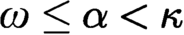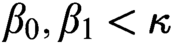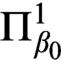Articles
DECIDING SOME MALTSEV CONDITIONS IN FINITE IDEMPOTENT ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2020, pp. 539-562
-
- Article
- Export citation
EXACT COMPLETION AND CONSTRUCTIVE THEORIES OF SETS
- Part of:
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 563-584
-
- Article
-
- You have access
- Open access
- Export citation
THE KETONEN ORDER
- Part of:
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 585-604
-
- Article
- Export citation
COMPUTABLE LINEAR ORDERS AND PRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 20 July 2020, pp. 605-623
-
- Article
- Export citation
VOICULESCU’S THEOREM FOR NONSEPARABLE
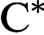 $\text{C}^{\ast} $
-ALGEBRAS
$\text{C}^{\ast} $
-ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 20 July 2020, pp. 624-631
-
- Article
-
- You have access
- Open access
- Export citation
ON OBDD-BASED ALGORITHMS AND PROOF SYSTEMS THAT DYNAMICALLY CHANGE THE ORDER OF VARIABLES
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2020, pp. 632-670
-
- Article
- Export citation
THE EXPONENTIAL DIOPHANTINE PROBLEM FOR
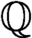 ${\mathbb {Q}}$
${\mathbb {Q}}$
- Part of:
-
- Published online by Cambridge University Press:
- 21 July 2020, pp. 671-672
-
- Article
- Export citation
CODING IN GRAPHS AND LINEAR ORDERINGS
- Part of:
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 673-690
-
- Article
- Export citation
ON CONFIGURATIONS CONCERNING CARDINAL CHARACTERISTICS AT REGULAR CARDINALS
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2020, pp. 691-708
-
- Article
- Export citation
HOW STRONG ARE SINGLE FIXED POINTS OF NORMAL FUNCTIONS?
- Part of:
-
- Published online by Cambridge University Press:
- 20 July 2020, pp. 709-732
-
- Article
- Export citation
THE COMPLEXITY OF HOMEOMORPHISM RELATIONS ON SOME CLASSES OF COMPACTA
- Part of:
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 733-748
-
- Article
- Export citation
INTERPRETABILITY LOGICS AND GENERALISED VELTMAN SEMANTICS
- Part of:
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 749-772
-
- Article
- Export citation
A REFINEMENT OF THE RAMSEY HIERARCHY VIA INDESCRIBABILITY
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2020, pp. 773-808
-
- Article
- Export citation
N-BERKELEY CARDINALS AND WEAK EXTENDER MODELS
- Part of:
-
- Published online by Cambridge University Press:
- 21 July 2020, pp. 809-816
-
- Article
- Export citation
HOMOGENEOUS STRUCTURES WITH NONUNIVERSAL AUTOMORPHISM GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2020, pp. 817-827
-
- Article
- Export citation
EQUATIONAL THEORIES OF FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 15 July 2020, pp. 828-851
-
- Article
- Export citation
FIRST-ORDER RECOGNIZABILITY IN FINITE AND PSEUDOFINITE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 20 July 2020, pp. 852-867
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JSL volume 85 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 27 January 2021, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JSL volume 85 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 27 January 2021, pp. b1-b2
-
- Article
-
- You have access
- Export citation