Research Article
A saturation property of ideals and weakly compact cardinals1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 513-525
-
- Article
- Export citation
Small filter forcing
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 526-546
-
- Article
- Export citation
Between strong and superstrong
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 547-559
-
- Article
- Export citation
On ideals of subsets of the plane and on Cohen reals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 560-569
-
- Article
- Export citation
Attention à la marche!
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 570-585
-
- Article
- Export citation
Completeness theorem for biprobability models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 586-590
-
- Article
- Export citation
Large cardinal structures below ℵω
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 591-603
-
- Article
- Export citation
Pκλ combinatorics II: The RK ordering beneath a supercompact measure
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 604-616
-
- Article
- Export citation
Distributive ideals and partition relations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 617-625
-
- Article
- Export citation
On the proof theory of the intermediate logic MH1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 626-647
-
- Article
- Export citation
On precipitousness of the nonstationary ideal over a supercompact
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 648-662
-
- Article
- Export citation
The truth is never simple
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 663-681
-
- Article
- Export citation
Taking out LK parts from a proof in Peano arithmetic1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 682-700
-
- Article
- Export citation
Supercompact cardinals, trees of normal ultrafilters, and the partition property1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 701-708
-
- Article
- Export citation
Some remarks on definable equivalence relations in O-minimal structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 709-714
-
- Article
- Export citation
The independence relation in separably closed fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 715-725
-
- Article
- Export citation
Small decidable sheaves
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 726-731
-
- Article
- Export citation
Some elementary degree-theoretic reasons why structures need similarity types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 732-747
-
- Article
- Export citation
Some properties of epistemic set theory with collection
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 748-754
-
- Article
- Export citation
Stability theory for topological logic, with applications to topological modules1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 755-769
-
- Article
- Export citation



 is a
is a  be any proper ideal of subsets of the real line
be any proper ideal of subsets of the real line  as follows:
as follows:  ⊂
⊂ 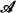 be a countable admissible set and
be a countable admissible set and 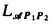 is similar to the standard probability logic
is similar to the standard probability logic 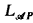 . The only difference is that two types of probability quantifiers
. The only difference is that two types of probability quantifiers 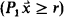 and
and 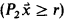 are allowed.
are allowed.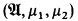 ,
, 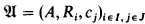 is a classical structure without operations and
is a classical structure without operations and 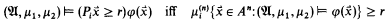
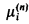 is the restriction of the completion of
is the restriction of the completion of 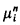 to the
to the 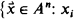
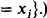
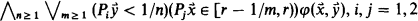 .
.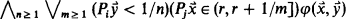 .
.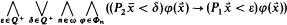
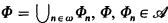 and
and 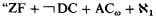
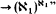 . Thus, consequences of AD whose consistency strength appeared to be beyond that of the more standard large cardinal hypotheses were shown to have suprisingly weak consistency strength.
. Thus, consequences of AD whose consistency strength appeared to be beyond that of the more standard large cardinal hypotheses were shown to have suprisingly weak consistency strength.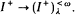
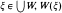 denotes the unique member of
denotes the unique member of 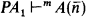 for each natural number
for each natural number 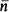 ) with length ≤
) with length ≤ 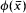 ∈
∈ 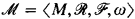 , where
, where 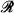 and
and 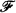 are disjoint sets,
are disjoint sets, 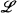 (with identity) has been specified, with constant symbols
(with identity) has been specified, with constant symbols 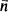 ,
,  . We wish to consider the variation in the
. We wish to consider the variation in the