Survey/expository paper
On Gödel's theorems on lengths of proofs I: Number of lines and speedup for arithmetics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 737-756
-
- Article
- Export citation
Research Article
The topological Vaught's conjecture and minimal counterexamples
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 757-784
-
- Article
- Export citation
A small reflection principle for bounded arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 785-812
-
- Article
- Export citation
More about relatively lawless sequences
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 813-829
-
- Article
- Export citation
A logic for approximate reasoning
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 830-837
-
- Article
- Export citation
Finitely axiomatizable ℵ1 categorical theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 838-844
-
- Article
- Export citation
Kernel contraction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 845-859
-
- Article
- Export citation
Chains and antichains in interval algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 860-867
-
- Article
- Export citation
Almost weakly 2-generic sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 868-887
-
- Article
- Export citation
A modal view of linear logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 888-899
-
- Article
- Export citation
On reduction properties
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 900-911
-
- Article
- Export citation
Connections between axioms of set theory and basic theorems of universal algebra
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 912-923
-
- Article
- Export citation
Bisimulations and predicate logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 924-944
-
- Article
- Export citation
A functorial property of the Aczel-Buchholz-Feferman function
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 945-955
-
- Article
- Export citation
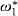 as an initial segment of the c-degrees
as an initial segment of the c-degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 956-976
-
- Article
- Export citation
Models of arithmetic and upper bounds for arithmetic sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 977-983
-
- Article
- Export citation
Constructing strongly equivalent nonisomorphic models for unsuperstable theories, Part A
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 984-996
-
- Article
- Export citation
Combinatorics on ideals and axiom A
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 997-1000
-
- Article
- Export citation
A feasible theory for analysis
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1001-1011
-
- Article
- Export citation
Flat sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1012-1021
-
- Article
- Export citation



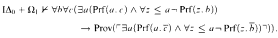
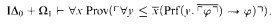
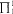 over certain transition predicates computable in log space), and (ii) as a tool for analyzing the dependence of transitions on data (which can be shown to be elementary or nonelementary, depending on the formulation of the transitions).
over certain transition predicates computable in log space), and (ii) as a tool for analyzing the dependence of transitions on data (which can be shown to be elementary or nonelementary, depending on the formulation of the transitions).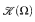 be the category where the objects are the countable ordinals and where the morphisms are the strictly monotonic increasing functions. A
be the category where the objects are the countable ordinals and where the morphisms are the strictly monotonic increasing functions. A 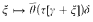 is a dilator for every
is a dilator for every 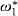 as an initial segment of the
as an initial segment of the 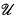 denotes a nonprincipal ultrafilter and
denotes a nonprincipal ultrafilter and 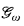 for ℙ(
for ℙ(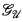 and showing that
and showing that 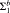 -graphs) of this theory are the polynomial time computable functions. It is shown that the first-order strength of this version of WKL is exactly that of the scheme of collection for bounded formulae.
-graphs) of this theory are the polynomial time computable functions. It is shown that the first-order strength of this version of WKL is exactly that of the scheme of collection for bounded formulae.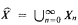 be the superstructure of
be the superstructure of 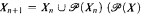 is the
is the 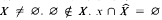 for each
for each 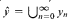 is the superstructure of
is the superstructure of 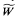 is an ultrapower of
is an ultrapower of 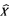 (generated by
(generated by