Research Article
On recursive enumerability with finite repetitions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 927-945
-
- Article
- Export citation
Model completeness of the new strongly minimal sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 946-962
-
- Article
- Export citation
Laver sequences for extendible and super-almost-huge cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 963-983
-
- Article
- Export citation
The ground-negative fragment of first-order logic is
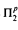 -complete
-complete
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 984-990
-
- Article
- Export citation
Un principe d'ax-kochen-ershov pour des structures intermédiates entre groupes et corps valués
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 991-1027
-
- Article
- Export citation
An elementary definability theorem for first order logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1028-1036
-
- Article
- Export citation
Implicit measurements of dynamic complexity properties and splittings of speedable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1037-1064
-
- Article
- Export citation
Jónsson cardinals, Erdős cardinals, and the core model
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1065-1086
-
- Article
- Export citation
A finite family weak square principle
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1087-1110
-
- Article
- Export citation
Heights of models of ZFC and the existence of end elementary extensions II
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1111-1124
-
- Article
- Export citation
There exist exactly two maximal strictly relevant extensions of the relevant logic R
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1125-1154
-
- Article
- Export citation
Forking and fundamental order in simple theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1155-1158
-
- Article
- Export citation
Freeness in classes without equality
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1159-1194
-
- Article
- Export citation
The emptiness problem for intersection types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1195-1215
-
- Article
- Export citation
Hyperfinite type structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1216-1242
-
- Article
- Export citation
Combinatorial properties of filters and open covers for sets of real numbers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1243-1260
-
- Article
- Export citation
Flat Morley sequences
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1261-1279
-
- Article
- Export citation
Lascar and Morley ranks differ in differentially closed fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1280-1284
-
- Article
- Export citation
A weak Dodd-Jensen lemma
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1285-1294
-
- Article
- Export citation
Finite powers of strong measure zero sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1295-1306
-
- Article
- Export citation



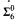 -complete.
-complete.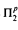 -complete
-complete
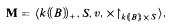
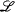 , then, clearly, any definable subset
, then, clearly, any definable subset  ] such that either
] such that either 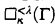 , we mean the principle asserting that there is a sequence 〈
, we mean the principle asserting that there is a sequence 〈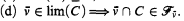
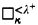 we mean
we mean 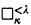 . If Γ = (κ, κ
. If Γ = (κ, κ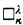 , which are equivalent to
, which are equivalent to 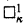 and
and  respectively. Jensen's global □ principle implies □
respectively. Jensen's global □ principle implies □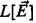 is a core model. Assume that every countable premouse
is a core model. Assume that every countable premouse 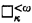 holds in
holds in 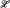 of real numbers have the covering property of Menger if, and only if, each filter on ω associated with its countable ω-cover is a P
of real numbers have the covering property of Menger if, and only if, each filter on ω associated with its countable ω-cover is a P