Research Article
Partition properties of M-ultrafilters and ideals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 897-907
-
- Article
- Export citation
Minimality in the Δ⅓-degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 908-915
-
- Article
- Export citation
Polynomial size proofs of the propositional pigeonhole principle
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 916-927
-
- Article
- Export citation
Gap-2 morasses of height ω
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 928-938
-
- Article
- Export citation
A constructive analysis of RM
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 939-951
-
- Article
- Export citation
Uncountable master codes and the jump hierarchy
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 952-958
-
- Article
- Export citation
On two hierarchies of dimensions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 959-968
-
- Article
- Export citation
Categorical semantics for higher order polymorphic lambda calculus
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 969-989
-
- Article
- Export citation
On the Rowbottom M-ultrafilters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 990-993
-
- Article
- Export citation
Corps portant un nombre fini de valuations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 994-1004
-
- Article
- Export citation
Properties of subtle cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1005-1019
-
- Article
- Export citation
Omitting types and the real line
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1020-1026
-
- Article
- Export citation
Théories d'algèbres de Boole munies d'idéaux distingués. I: Théories élémentaires
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1027-1043
-
- Article
- Export citation
Reviews
Handbook of set-theoretic topology, edited by Kenneth Kunen and Jerry E. Vaughan, North-Holland, Amsterdam, New York, and Oxford, 1984, vii + 1273 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1044-1046
-
- Article
- Export citation
Errett Bishop and Douglas Bridges. Constructive analysis. Grundlehren der mathematischen Wissenschaften, no. 279. Springer-Verlag, Berlin, Heidelberg, New York, and Tokyo, 1985, xii + 477 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1047-1048
-
- Article
- Export citation
James M. Henle. An outline of set theory. Problem books in mathematics. Springer-Verlag, New York, Berlin, etc., 1986, viii + 145 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1048-1049
-
- Article
- Export citation
žarko Mijajlović, Zoran Marković, and Kosta Dos̄en. Hilbertovi problemi i logika (Hilbert's problems and logic). Matematic̆ka biblioteka, no. 48. Zavod za Udžbenike i Nastavna Sredstva, Belgrade1986, 168 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1049-1050
-
- Article
- Export citation
Fred Feldman. Doing the best we can. An essay in informal deontic logic. Philosophical studies series in philosophy, vol. 35. D. Reidel Publishing Company, Dordrecht, Boston, Lancaster, and Tokyo, 1986, xiv + 244 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1050-1051
-
- Article
- Export citation
Anthony Appiah. Assertion and conditionals. Cambridge studies in philosophy. Cambridge University Press, Cambridge etc. 1985, xiii + 265 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1051-1052
-
- Article
- Export citation
Stuart M. Shieber. An introduction to unification-based approaches to grammar. CSLI lecture notes, no. 4. Center for the Study of Language and Information, Stanford 1986, also distributed by the University of Chicago Press, Chicago, iv + 105 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1052-1054
-
- Article
- Export citation



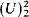 ;
;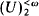 .
. and
and 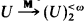 for
for 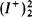 and
and 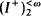 (Definition 2.3) of uniform ideals
(Definition 2.3) of uniform ideals 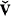 -ultrafilter in the Boolean-valued model constructed from the completion of the quotient algebra P(
-ultrafilter in the Boolean-valued model constructed from the completion of the quotient algebra P(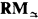 (Sobociński 3-valued logic; see [4]). Anderson and Belnap admit [1, p. 149] that this fact came to them as a distinct surprise, since
(Sobociński 3-valued logic; see [4]). Anderson and Belnap admit [1, p. 149] that this fact came to them as a distinct surprise, since 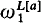 .
. , set-theoretically as the degree of the
, set-theoretically as the degree of the  nonisolated types. But MA is rather a strong axiom. We prove that in order to be able to omit <
nonisolated types. But MA is rather a strong axiom. We prove that in order to be able to omit <