Research Article
A noninitial segment of index sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 209-224
-
- Article
- Export citation
Correction
Correction to ‘A model theoretic characterisation of effective operations’
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 225
-
- Article
- Export citation
Research Article
Combinator realizability of a constructive Morse set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 226-234
-
- Article
- Export citation
Sets of theorems with short proofs
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 235-242
-
- Article
- Export citation
Systems of notations and the ramified analytical hierarchy
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 243-253
-
- Article
- Export citation
Boolean extensions which efface the Mahlo property1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 254-268
-
- Article
- Export citation
On projective ordinals1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 269-282
-
- Article
- Export citation
Nonrecursive tilings of the plane. I
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 283-285
-
- Article
- Export citation
Nonrecursive tilings of the plane. II
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 286-294
-
- Article
- Export citation
Σn sets which are Δn-incomparable (uniformly)1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 295-304
-
- Article
- Export citation
Recursively presentable prime models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 305-309
-
- Article
- Export citation
Analytic inductive definitions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 310-312
-
- Article
- Export citation
The λ-calculus is ω-incomplete
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 313-317
-
- Article
- Export citation
On existence proofs of Hanf numbers1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 318-324
-
- Article
- Export citation
Reviews
Mircea Tîrnoveanu. Elemente de logicǎ matematicǎ. Vol. 1. Logicǎ propoziţülor bivalente. (Elements of mathematical logic. Vol. 1. Logic of bivalent propositions.) Editura Didacticǎ şi Pedagogicǎ, Bucharest 1964, 519 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 325-327
-
- Article
- Export citation
Evandro Agazzi. La logica simbolica. Editrice La Scuola, Brescia 1964, 396 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 327-328
-
- Article
- Export citation
J. Barkley Rosser. Simplified independence proofs. Boolean valued models of set theory. Pure and applied mathematics, no. 31. Academic Press, New York and London 1969, xv + 217 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 328-329
-
- Article
- Export citation
R. M. Solovay and S. Tennenbaum. Iterated Cohen extensions and Souslin's problem. Annals of mathematics, ser. 2 vol. 94 (1971), pp. 201–245.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 329-330
-
- Article
- Export citation
Gerald E. Sacks. Forcing with perfect closed sets. Axiomatic set theory, Proceedings of symposia in pure mathematics, vol. 13 part 1, American Mathematical Society, Providence, Rhode Island, 1971, pp. 331–355.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 330
-
- Article
- Export citation
Robert M. Solovay On the cardinality of sets of reals. Foundations of mathematics, Symposium papers commemorating the sixtieth birthday of Kurt Gödel, edited by Jack J. Bulloff, Thomas C. Holyoke, S. W. Hahn, Springer-Verlag, Berlin, Heidelberg, and New York, 1969, pp. 58–73.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 330
-
- Article
- Export citation



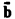 the one-one degree of
the one-one degree of 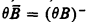 . Let
. Let 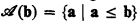 . Let {
. Let {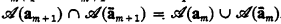 .
.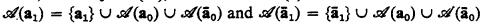 .
.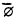 ,
, 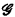 of type
of type 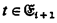 to satisfy the additional condition
to satisfy the additional condition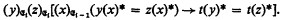
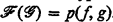 for all effective operations
for all effective operations 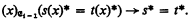
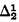 ordinals). Arithmetic minimality means that if
ordinals). Arithmetic minimality means that if 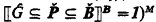 (cf. [11, p. 361] and [3, pp. 58–59]), and for
(cf. [11, p. 361] and [3, pp. 58–59]), and for 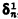 , where
, where 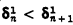 , for all even
, for all even 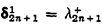 , where λ
, where λ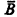 when one feeds in
when one feeds in 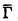 is Γ
is Γ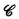 be a class of operators over the natural numbers. The closure ordinal ∣
be a class of operators over the natural numbers. The closure ordinal ∣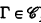 }. The closure algebra
}. The closure algebra 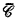 generated by
generated by 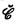 generated by
generated by 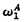 is the supremum of the ordinals of well-orderings recursive in
is the supremum of the ordinals of well-orderings recursive in 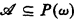 , let
, let 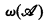 be the supremum of
be the supremum of 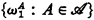 . For example, it is well known that
. For example, it is well known that 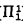 ) =
) = 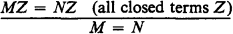
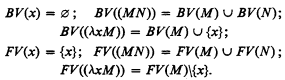
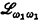 positively. We conclude by showing that the existence of a Hanf bound for
positively. We conclude by showing that the existence of a Hanf bound for