Research Article
Sub-Temperate Basal Sliding
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 3-5
-
- Article
-
- You have access
- HTML
- Export citation
A Numerical Study of Plane Ice-Sheet Flow
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 139-160
-
- Article
-
- You have access
- HTML
- Export citation
Chemical Fractionation of Brine in the McMurdo Ice Shelf, Antarctica
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 307-313
-
- Article
-
- You have access
- HTML
- Export citation
On the Deterioration of a Grounded Iceberg
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 161-167
-
- Article
-
- You have access
- HTML
- Export citation
Icing on a Non-Rotating Cylinder Under Conditions of High Liquid Water Content in the Air: I. Form and Size of Ice Deposits
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 6-11
-
- Article
-
- You have access
- HTML
- Export citation
Explosive Growth of Shear-Heating Instabilities in the Down-Slope Creep of Ice Sheets
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 314-320
-
- Article
-
- You have access
- HTML
- Export citation
Icing on a Non-Rotating Cylinder Under Conditions of High Liquid Water Content in the Air: II. Heat Transfer and Rate of Ice Growth
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 12-19
-
- Article
-
- You have access
- HTML
- Export citation
Comparison of Experimental and Computer Modeling of Snow-Block Impact on Structures
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 321-324
-
- Article
-
- You have access
- HTML
- Export citation
Theory and Laboratory Observations of Naled Ice Growth
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 168-177
-
- Article
-
- You have access
- HTML
- Export citation
Subglacial Hydrology for an Ice Sheet Resting on a Deformable Aquifer
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 20-30
-
- Article
-
- You have access
- HTML
- Export citation
Propagating Strain Anomalies during Mini-Surges of Variegated Glacier, Alaska, U.S.A.
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 178-191
-
- Article
-
- You have access
- HTML
- Export citation
Wave Ogives
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 325-334
-
- Article
-
- You have access
- HTML
- Export citation
Refraction Correction for Radio Echo-Sounding of Ice Overlain by Firn
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 192-194
-
- Article
-
- You have access
- HTML
- Export citation
Drainage-Basin Characteristics of Nordaustlandet Ice Caps, Svalbard
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 31-38
-
- Article
-
- You have access
- HTML
- Export citation
Stress-Gradient Coupling in Glacier Flow:III. Exact Longitudinal Equilibrium Equation*
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 335-341
-
- Article
-
- You have access
- HTML
- Export citation
Interpretation of Radio Echoes from Storglaciären, Northern Sweden
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 39-49
-
- Article
-
- You have access
- HTML
- Export citation
Discharges of Turbid Water during Mini-Surges of Variegated Glacier, Alaska, U.S.A.
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 195-207
-
- Article
-
- You have access
- HTML
- Export citation
Stress-gradient Coupling in Glacier Flow: IV. Effects of the “T” Term*
-
- Published online by Cambridge University Press:
- 12 May 2017, pp. 342-349
-
- Article
-
- You have access
- HTML
- Export citation
Medial Moraines and Surface Melt on Glaciers of the Torngat Mountains, Northern Labrador, Canada
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 350-354
-
- Article
-
- You have access
- HTML
- Export citation
Assessment of mass-balance variations within a sparse stake network, qamanârssûp sermia, west greenland
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 50-53
-
- Article
-
- You have access
- HTML
- Export citation




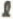 is increased by about 5%. 2. The asymmetry parameter
is increased by about 5%. 2. The asymmetry parameter 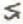 2.5
2.5