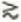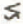1. Introduction
In the “vertically” integrated stress-equilibrium equation for a limitlessly wide glacier or ice sheet flowing in plane strain over a basal surface of longitudinally varying slope, as discussed by Reference KambKamb (1986), there occurs a term often designated “T” and given by

where x is a longitudinal coordinate, y is generally upward normal to x, and y B and y s are the y coordinates of the bed and surface. This term was formulated and discussed in a series of papers by Reference BuddBudd (1968, Reference Budd1970[a], Reference Budd[b], Reference Budd1971), who called it the “variational stress” term. Its role in longitudinal stress equilibrium as presently understood has been summarized by Reference NyeNye (1969, p. 212), Reference Raymond and VoightRaymond (1978, p. 808; 1980, p. 104), and Reference PatersonPaterson (1981, p. 100 and 164), who quoted Budd’s conclusion that T is negligible when averaged longitudinally over distances greater than 3h‒4h, where h is the ice thickness. On the other hand, Reference BuddBudd (1971, p. 186) stated, on the basis of a calculation of flow over sinusoidal bedrock topography of wavelength λ, that “for wavelengths λ = 4h or less the T term cannot be neglected”.
In the theory of longitudinal stress-gradient coupling developed by Reference Kamb and EchelmeyerKamb and Echelmeyer (1986) in Part I it was found that glacier flow is governed by a longitudinal average of ice thickness and surface slope weighted in such a way that most of the contribution to the average comes from a longitudinal interval 2
2. Effect of T on Longitudinal Equilibrium
The effect of the T term in the longitudinal equilibrium equation (23) of Part III (Reference KambKamb, 1986) (hereafter designated (111-23)) can be determined by introducing into Equation (1) the longitudinal variation in τ xy , that necessarily arises in the context of the theory in Parts I and II when the basal shear stress τ B varies with x. Consistent with the assumptions in equations (1-1) and (1–2) (from Part I) as to how flow and stress are related, the longitudinal variation in τ xy is linked to the longitudinal variation in τ B by assuming that τ xy varies linearly with y from the bed to the surface, as if would exactly if the longitudinal stress gradient ∂τ xx /∂x were independent of y. Hence we take

τ B(x) is the quantity whose departure from the value ρghα (where α is the local slope) the theory in Part I implicitly calculates from the effect of longitudinal stress gradients. By making τ xy (y S) = 0 in Equation (2) we neglect the small amount, of order δ, by which it differs from 0 because the surface is inclined at angle δ (assumed small) to the x-axis. Figure 1 in Part III shows the flow geometry and the angles δ = +dy s /dx and θ = +dy B /dx, the latter being the slope of the bed relative to the x-axis, also assumed small.
If we now perform on Equation (2) the x differentiations and then the y integrations indicated in Equation (1), and define dh/dx = × ≅ +(δ ‒ θ), we obtain after some manipulation

We then introduce Equation (3) into the equilibrium equation (III-23), obtaining, after re-arrangement

If we make the small-angle approximation δ ~ – « 1, then, as discussed in Part III, section 9, the terms B and K can be dropped, and the right-hand side of Equation (4a) reduces to

3. Effect on the Longitudinal Flow Coupling Equation of Part I
We now proceed from Equation (4) to the longitudinal flow-coupling equation by the same steps used in Part I, sections 2 and 3, starting from Equation (I – 4). First, we calculate the derivatives of τ B in terms of the flow ū from Equation (I-1):


Then we apply the perturbation treatment described in Part I, section 3, putting v = (u‒u 0)/u 0. This treatment involves a datum state in which all the derivatives in Equations (5) and (6) are zero. Thus the perturbed forms of Equations (5) and (6) are


where τ 0 = (u 0/c 1 h 0)1/n . When Equations (7) and (8) are substituted into Equation (4), we obtain the longitudinal flow-coupling equation with inclusion of the effects of the T term:

In the bracketed coefficient on the right in Equation (9) the second-order terms in – and δ can be neglected at our level of approximation, but the curvature terms have to be retained at this level. If we assume that since v is treated as a small perturbation, the term in (dv/dx)2 can be neglected, and if we multiply through by n/τ 0 in Equation (9) and gather terms, we obtain the equivalent of the longtudianl flow-coupling equation (I-10), corrected by addition of terms coming from T:

where ![]() is as defined in equation (I-11). Here we have replaced χ by dh/dx.
is as defined in equation (I-11). Here we have replaced χ by dh/dx.
For a convenient overview we can rewrite Equation (10) in the condensed form

where



4. Evaluation of Effects of the T Term
The effects of the T term on the longitudinally coupled flow are exhibited by Equation (11), which is similar in form to equation (I-10), with modifications as follows:
-
1. The longitudinal coupling length
 is increased to
is increased to  as given by Equation (12). In view of the
as given by Equation (12). In view of the  /h
0 values given in Part I, table I, this increase is a small effect, amounting at most to a few per cent.
/h
0 values given in Part I, table I, this increase is a small effect, amounting at most to a few per cent. -
2. The asymmetry parameter σ, given by equation (I-12), is changed to σ’ in Equation (13). To assess easily the effect of this change, it is helpful to define by σ h the contribution to σ from the longitudinal gradient of ice thickness in equation (I-12),
(16a)
which is what was used in calculating σ values for Part II, table I, and also to define a similarly scaled quantity deriving from the surface topography
(16b)
With Equation (16a) and (16b), σ’ from Equation (13) can be expressed as
(17)
Since σ, σh, and σα are of the same order of size, and since
 ≈1 while h
0/
is a fraction of unity (Part I, table I), σ’ differs from σ by only a modest fraction, in general.
≈1 while h
0/
is a fraction of unity (Part I, table I), σ’ differs from σ by only a modest fraction, in general.
-
3. The C(x) term on the right in Equation (11) is a forcing term that affects the flow via longitudinal averaging in a way similar to the effects of slope and thickness from the F(x) term on the right, already treated in Part I. We may call it the “T force”. It arises from longitudinal curvature of the surface and/or bed. The form of C(x) in Equation (15) is obtained from Equation (10) by noting that α = δ +
 and d/dx = 0,
and d/dx = 0,
 being the slope of the x-axis. To assess the magnitude of the effects of C(x) it is helpful to expand Equation (14) and re-group the terms on the right side of Equation (11) as follows:
(18)
being the slope of the x-axis. To assess the magnitude of the effects of C(x) it is helpful to expand Equation (14) and re-group the terms on the right side of Equation (11) as follows:
(18)
where H(x) is a forcing term due to thickness variations and A(x) is a forcing term due to slope variations. Equation (18) utilizes the fact that for the perturbation considered, dh/dx = dΔh/dx and dα/dx = dΔα/dx.
If we take harmonic variations of slope and thickness

(where the phase shift Φ is arbitary), then


Form Equation (20a) we see that the effect of the T term is to enhance H(x) by the factor 1 + (2πh
0/λ)2/6. This enhancement of the influence of longitudinal variations in ice thickness on flow is a new effect, not previously recognized in glacier-flow mechanics. Its physical basis is subtle and not immediately obvious but it can be understood in detail by tracing its origin back to the terms in the equilibrium equations from which it springs. The enhancement factor is 2 for λ = 2.6h, while for λ = 8.1h the factor has fallen to 1.1. The enhancement cannot be considered negligible at the 10% level except for λ ![]() 8 h. However, the effect of longitudinal stress-gradient coupling in attenuating the flow variations at short wavelengths works to suppress strongly the flow variations that tend to be enhanced by the “T force”. Thus, from Part I, section 3, longitudinal averaging causes attenuation of the flow response to Equation (20) by a factor (1 + (2π
8 h. However, the effect of longitudinal stress-gradient coupling in attenuating the flow variations at short wavelengths works to suppress strongly the flow variations that tend to be enhanced by the “T force”. Thus, from Part I, section 3, longitudinal averaging causes attenuation of the flow response to Equation (20) by a factor (1 + (2π

Since ![]() ≈ 2h (see Part I), Equation (21a) indicates that when the enhancement factor due to the T term is 1.4, the attenuation factor due to longitudinal averaging is 0.1, which nearly eliminates the response wave.
≈ 2h (see Part I), Equation (21a) indicates that when the enhancement factor due to the T term is 1.4, the attenuation factor due to longitudinal averaging is 0.1, which nearly eliminates the response wave.
In the short-wavelength limit, as λ → 0, the response in Equation (21a) tends to

This short-wavelength response is (h 0/
A second, more practically oriented reason for disregarding this effect is that the percentage variations in ice thickness at relatively short wavelengths are typically small compared to the percentage variations in slope, so that most of the longitudinal variation in the input function F(x) + C(x) comes from the slope function A(x) rather than from the thickness function H(x). Thus, for Variegated Glacier (Part I, fig. 8), the variations in h(x) at wavelengths ![]() 1000 m are less than about 5%, whereas the variations in α(x) are 20-100%. A large variation in h(x) occurs over a half wavelength equal to the length of the glacier, of course, but for this variation λ/h ~ 100 and the T-term correction to H(x) in Equations (18) or (20a) is completely negligible. Blue Glacier (Part I, fig. 10) is similar except that there is a large variation in h connected with the ice fall, over a length scale ~1 km.
1000 m are less than about 5%, whereas the variations in α(x) are 20-100%. A large variation in h(x) occurs over a half wavelength equal to the length of the glacier, of course, but for this variation λ/h ~ 100 and the T-term correction to H(x) in Equations (18) or (20a) is completely negligible. Blue Glacier (Part I, fig. 10) is similar except that there is a large variation in h connected with the ice fall, over a length scale ~1 km.
The T-term correction to the slope-input function A(x) in Equation (20b), contained in the second term on the right, is a wave shifted 90° in phase relative to the direct input from F(x). This flow effect is again new and has a physical basis very similar to the T-term enhancement of H(x) in Equation (20a). Again, from Part I, section 3, the flow response to A(x) in Equation (20b) will be

where ψ = tan-1 (π α0 h 0/λ). The “T force” causes enhancement of the response by the square-root factor in the numerator, and longitudinal coupling superimposes an attenuation factor, the reciprocal of the quantity in the denominator. For Variegated Glacier, with α0 ≈ 0.1 and λ ≈ 950 m ≈ 2.7h for the typical longitudinal oscillations in α (Part I, fig. 8), the enhancement factor is only 1.01, and the attenuation factor is 1/23. For λ = 1.3h, corresponding to the shortest wavelength oscillations in a, the enhancement factor is still only 1.03, while the attenuation factor is 1/94. Thus the effects of enhancement of A(x) due to the “T force” appear quite negligible. Even for a large mean slope α0 ~ 0.5, the effects are probably not large enough to be recognizable in an observed flow response.
The above conclusions, based on the theoretical results for harmonic perturbations in Equations (20)‒(22), are tested in a practical way by direct calculation of the effect of the forcing term C(x) on the flow curves of Variegated Glacier and Blue Glacier that were obtained in Part I, sections 8 and 9, with C(x) omitted. From the functions h(x) and α(x) used there, we calculate C(x) from Equation (15), add it to the input function F(x) used previously, and carry out the longitudinal averaging by the same method and with the same parameter values used in Part I, sections 8 and 9. For Variegated Glacier, the flow as so recalculated differs by at most 1% from the calculated flow curve for 4
From the foregoing considerations, we conclude that in the first-approximation treatment of Part I the effects of the T term contained in the function C(x) are essentially negligible. In a higher approximation it might be appropriate to use the modified form of H(x) in Equation (18) and to seek observational evidence for effects of the enhancement factor in Equation (20a). In cases of high surface slope (α ![]() 0.5), the enhancement of A(x) indicated by Equation (20b) might possibly need to be taken into consideration.
0.5), the enhancement of A(x) indicated by Equation (20b) might possibly need to be taken into consideration.
5. Effect on the Basal Shear Stress
Because of the direct linkage between flow velocity and basal shear stress via equation (I‒1), the conclusions of the last section are tantamount to the conclusion that the T term has an essentially negligible effect on τB. The maximum effect on τB is for short-wavelength variations in ice thickness h; in this case the T term gives a variation in τB that is about 4% of the variation of the local “slope stress” ρgαh, according to Equation (21b) with ![]() ≈2h. (As noted in section 4, the accuracy of this estimate is limited by the validity of the underlying assumption in Equation (2), which declines at short wavelengths.) Variations in slope α have a smaller effect via the T term, as long as the slopes are relatively small (α0~0.1.) If effects at the
≈2h. (As noted in section 4, the accuracy of this estimate is limited by the validity of the underlying assumption in Equation (2), which declines at short wavelengths.) Variations in slope α have a smaller effect via the T term, as long as the slopes are relatively small (α0~0.1.) If effects at the ![]() 5% level can be neglected, the relation between slope stress and τB remains as given by equation (1‒34) without modification from the T term.
5% level can be neglected, the relation between slope stress and τB remains as given by equation (1‒34) without modification from the T term.
This means that it is not necessary to distinguish between two longitudinal length scales for averaging of τB ‒ a short scale over which the effects of T are significant and an intermediate scale over which they are negligible ‒ as has often been done in the literature (for summary see Reference Raymond and VoightRaymond (1978, p. 809)). There still remains the need to distinguish between a short scale over which longitudinal stress gradients significantly affect τB and a long scale over which they do not, as discussed in part 1, section 3.
6. Comparison with other Evaluations of T
The evaluation of the T term given by Reference BuddBudd (1968, p. 64) and recapitulated by Reference HutterHutter ([c1983], p. 265) is based on the simple assumption that τ xy (y) in Equation (1) is given by ρgα(y S‒y). This is incorrect. Because of the effect of longitudinal stress gradients, τ xy (x.y) is everywhere modified from the value ρgα(y S‒y) that it would have in the absence of these gradients. The mistaken asusmption leads to the conclusion that T varies as d2α/dx 2, whereas we see from Equation (10) that the “direct” contribution from T to the input function C(x) varies instead as dα/dx and d(α ‒ β)/dx. The source of this contribution is from the ratio (y s ‒y)/h in Equation (2), and is physically quite distinct from the effects of the factor τB(x) in Equation (2), which is, according to the present theory, what must replace ρghα in Budd’s evaluation. The second-derivative effect, from d2τB/dx 2 in Equation (3), appears ultimately in the contribution h 0 2/6 in Equation (12), which is the principal “indirect” effect of the T term on the flow. We see here how the flow coupling modulates in a significant and subtle way the flow response to α(x) and h(x) via the T term. These conclusions are, of course, limited by the validity of the assumption in Equation (2) on which evaluation of the T term is based, but this treatment, which takes into consideration in a first approximation the effect of longitudinal stress coupling on the T term, is obviously better than a treatment that does not, as is the case with Budd’s.
A second evaluation of the T term was given by Reference BuddBudd (1971, p. 185) along entirely different lines, based on a treatment of flow over sinusoidal bedrock topography by a linear-viscous analysis that in principle can be made exact for topographic undulations of infinitesimal amplitude. The basic idea is good, but, as pointed out by Reference Hutter, Hutter, Legerer and SpringHutter and others (1981, p. 252), Budd’s analysis is flawed by a fundamental error, which makes the results invalid. The magnitude of T given by Reference BuddBudd (1971, fig. 3) would indicate a contribution comparable to what we evaluate from Equation (15), although the detailed form of the dependence on λ is different and there is no indication of the phase shift relative to α(x) shown in Equation (21).
7. Effect of the T Term on the Longitudinal Flow-Coupling Equation of Part II
We now consider the effects of the T term on the flow perturbation that arises as a result of a small perturbation in ice thickness and surface slope from the realistic datum state of a glacier for which h, α, and u are known functions of x. This type of flow perturbation is the subject treated in Part II.
To find the effects of the T term, we need to evaluate the perturbation term T 1 in equation (II‒4). to find how it depends on the datum-state functions h 0 , α 0, and u 0 and on the perturbations h 1, α 1 and β1 introduced in Part II, section 2. If we continue to make the basic assumption contained in Equation (2), then the T term is given by Equation (3). To find the perturbation T1, we introduce into Equation (3) the perturbation relations τB = τ 0 + τ1 , h = h 0 + h 1 δ = δ 0 + α1, θ = θ0 + β 1, X = X 0 +X 1 = dh 0 /dx +dh 1 /dx, u = u 0 + u 1, and T = T 0 + T 1 and then subtract from Equation (3) the value of the unperturbed term T 0, obtained by setting all the perturbations to zero. Keeping only the first-order perturbation terms, we find

Now we express the perturbation τ1 in terms of the perturbations u 1 and h 1 by means of equation (I‒9), which can be rewritten

(overlooking the distinction between n and n’ discussed in Part 11, section 2). From Equation (24) we can also obtain the derivatives dτ1/dx and d2τ1/dx 2. When these are put into Equation (23) and related terms grouped (noting that X = dh/dx), we obtain

in which the coefficients t u , t h, etc. are the following functions of the datum-state variables:




If we now introduce T 1 from Equation (25) into equation (II‒6), we get a longitudinal coupling equation that contains the effects of the T 1 term. When the terms are grouped and designated as in equation (II‒13), this reads

where


and where ![]() is defined in equation (II‒11), b in Equation (II-7), and t
u
in Equation (26). Equation (30) has a form similar to Equation (II‒13). The modified coefficients ϕ’
h
, ϕ’α
, ets., on the right side of Equation (30) are given explicitly below, in Equations (36)–(40).
is defined in equation (II‒11), b in Equation (II-7), and t
u
in Equation (26). Equation (30) has a form similar to Equation (II‒13). The modified coefficients ϕ’
h
, ϕ’α
, ets., on the right side of Equation (30) are given explicitly below, in Equations (36)–(40).
8. Evaluation of Effects on Flow Response to a Perturbation in Ice Thickness and Slope
Of the numerous terms in Equation (30) that are not present in the longitudinal flow-coupling equation (11–13), the magnitudes of some can be judged from their order in the angle δo and the quantity χ0 = dh o/dx, while for others a specific evaluation based on the characteristics of actual datum states is required. For this purpose, we take the geometry and flow field of Blue Glacier as a representative example (Echelmeyer, unpublished; Part II, table II).
As indicated in Equation (33), the quantity b′, which is present as the factor 1/b′ in all coefficients on the right-hand side of Equation (30), is modified from b by the quantity tu in Equation (26). If δo is small, as is χo by assumption, then the first two terms on the right in Equation (26), which are second order in these angle quantities, are negligible, and b itself is negligibly different from 1. If h odχo/dx and h odlnu o/dx are small of order δo, as may often be the case in practice, then the third, fifth, and sixth terms in Equation (26) are negligible on the same basis. The remaining terms are best evaluated numerically. Using the Blue Glacier datum state, we calculate values of b′ in the range 0.98 to 1.03. At the level of approximation sought in Part II, b′ can thus be taken as unity.
In view of this, the modified longitudinal coupling length l″ given by Equation (31) differs inappreciably from the l′ in Equation (12), except for the effect of the n″ in equation (II–ll), which was already noted in Part II, section 2.
The modified symmetry parameter σ′ in Equation (32) can be expressed, in terms of Equations (16a), (16b), and the additional similar definition
as follows:
Equation (35) is an augmented version of Equation (17). If σu is comparable to σ, σh , and σ∝ , then the discussion of σ based on Equation (17) in section 4 applies equally well to σ″ in Equation (35).
The influence coefficients on the right-hand side of Equation (30) are modified from those given by Equations (II-8)–(II-10) as follows:

where th , tα , and tβ are given by Equations (27)–(29), and jα by Equations (II–27) and (II–28), and jβ by

In Equations (36)–(38) the quantity b′ has been set equal to 1.
The magnitude of the correction term th in Equation (36) is found, from Equation (27) evaluated with the Blue Glacier data, to be \th \ ≤ 0.04. ϕh′, therefore is dominated by the other terms in Equation (36). However, for longitudinal gradients of h 0, ∂ 0, or u 0 rather larger than those in the Blue Glacier datum state, the size of tβ could be large enough to have an appreciable influence.
While j∝ Equation (37) is small (as found in Part II, section 5), ta is not particularly small, being of order ∂0 or e0 according to Equation (28). However, the factor sin#x221D*; in Equation (37) reduces the magnitude of the product to ≤ 0.02, for the Blue Glacier datum state. The effect can thus be neglected in general for typical valley glaciers with sin#x221D*; ∼ 0.1, but for steep glaciers or ice falls it may be non-negligible. The correction term tβ in Equation (38) does not have the sin#x221D*; factor, and it appears that the β 1 response may be appreciably affected by the T term. From Equation (29) this could be evaluated for an actual situation in which a β 1 perturbation came into consideration.
The final two terms in Equation (30), with coefficients
and
are the same as the terms given by C(x) in Equation (15). Their role in a flow perturbation here will be quite the same as already discussed in section 4 above. From the Blue Glacier perturbation data the quantity –(h o/6)(d2 h l/dx 2) has extreme values 1.1%, −0.8%, and −0.6%, at points where h 1/h 0 has values 4.2%, 4.0%, and 7.0%, respectively, indicating that the “thickness-curvature term” can amount to as much as 25% of the direct h 1/h 0 term on the right side of Equation (30). More typically, however, it amounts to only about 3%. Longitudinal averaging tends to suppress the effect of the localized higher values, as discussed in section 4. The quantity h 0/2)dα1/dx is found, for the Blue Glacier data, to be smaller by a factor of about 10, and therefore negligible.
From the foregoing evaluation, we conclude that the effects of the T 1 term on flow perturbations can in general be neglected, but that we should be on the lookout for unusual datum-state situations in which one or more of the many quantities that the T 1 term generates in Equations (26)-(35) would happen to be large enough to need to be taken into consideration.
9. Role of the T Term in Short-Wavelength Longitudinal Flow Variations
The simple assumption in Equation (2) that τxy is a linear function of y, which leads to the conclusions of this paper as to the essentially negligible role of the T term in longitudinal stress coupling, is a reasonable first approximation for long wavelengths, but breaks down at short wavelengths λ ≲ h, as has been repeatedly pointed out in sections 4–6. In Part III, section 6, it is noted that in longitudinal flow variations at very short wavelengths (λ ≪ h) the T term plays a major role in the longitudinal equilibrium equation, as expected from the presence of the second derivative in Equation (1). The role of the T term in longitudinal coupling at short wavelengths will be explored further in a later paper, and it will be shown there that longitudinal coupling theory can be extended in an approximate but useful way to short wavelengths by taking effects of the T term into consideration.


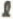 is increased by about 5%. 2. The asymmetry parameter
is increased by about 5%. 2. The asymmetry parameter 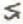 2.5
2.5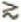
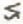
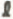 est accrue de 5% environ; (2) le paramètre d’asymétrie
est accrue de 5% environ; (2) le paramètre d’asymétrie 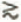
 wird etwa 5% grösser. 2. Der Asymmetrie-Parameter
wird etwa 5% grösser. 2. Der Asymmetrie-Parameter  2,5
2,5