Research Article
Chemical Fractionation of Brine in the McMurdo Ice Shelf, Antarctica
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 307-313
-
- Article
-
- You have access
- HTML
- Export citation
Explosive Growth of Shear-Heating Instabilities in the Down-Slope Creep of Ice Sheets
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 314-320
-
- Article
-
- You have access
- HTML
- Export citation
Comparison of Experimental and Computer Modeling of Snow-Block Impact on Structures
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 321-324
-
- Article
-
- You have access
- HTML
- Export citation
Wave Ogives
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 325-334
-
- Article
-
- You have access
- HTML
- Export citation
Stress-Gradient Coupling in Glacier Flow:III. Exact Longitudinal Equilibrium Equation*
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 335-341
-
- Article
-
- You have access
- HTML
- Export citation
Stress-gradient Coupling in Glacier Flow: IV. Effects of the “T” Term*
-
- Published online by Cambridge University Press:
- 12 May 2017, pp. 342-349
-
- Article
-
- You have access
- HTML
- Export citation
Medial Moraines and Surface Melt on Glaciers of the Torngat Mountains, Northern Labrador, Canada
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 350-354
-
- Article
-
- You have access
- HTML
- Export citation
Effects of the 1966–68 Eruptions of Mount Redoubt on the Flow of Drift Glacier, Alaska, U.S.A.
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 355-362
-
- Article
-
- You have access
- HTML
- Export citation
Isotropic Points on Glaciers
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 363-365
-
- Article
-
- You have access
- HTML
- Export citation
Implications of the form of the Flow Law for Vertical Velocity and Age–Depth Profiles in Polar Ice
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 366-370
-
- Article
-
- You have access
- HTML
- Export citation
Changes in the Salinity and Porosity of Sea-Ice Samples During Shipping and Storage
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 371-375
-
- Article
-
- You have access
- HTML
- Export citation
A Preliminary Assessment of Glacial Ice Profiling Using Vlf Surface-Impedance Measurements
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 376-382
-
- Article
-
- You have access
- HTML
- Export citation
Ice Conditions of an Arctic Polynya: North Water in Winter
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 383-390
-
- Article
-
- You have access
- HTML
- Export citation
Three-Dimensional Coordination Number from Two-Dimensional Measurements: A New Method
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 391-396
-
- Article
-
- You have access
- HTML
- Export citation
Experiments on Freeze-Bonding Between Ice Blocks in Floating Ice rubble
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 397-403
-
- Article
-
- You have access
- HTML
- Export citation
Motion of Sub-Freezing Ice Past Particles, with Applications to Wire Regelation and Frozen Soils
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 404-414
-
- Article
-
- You have access
- HTML
- Export citation
Grain Growth in Polar Ice: I. Theory
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 415-424
-
- Article
-
- You have access
- HTML
- Export citation
Grain Growth in Polar Ice: II. Application
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 425-433
-
- Article
-
- You have access
- HTML
- Export citation
The Granular Structure of Snow: An Internal-State Variable Approach
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 434-438
-
- Article
-
- You have access
- HTML
- Export citation
Hydraulics of Subglacial Cavities
-
- Published online by Cambridge University Press:
- 20 January 2017, pp. 439-445
-
- Article
-
- You have access
- HTML
- Export citation




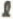 is increased by about 5%. 2. The asymmetry parameter
is increased by about 5%. 2. The asymmetry parameter 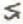 2.5
2.5