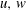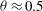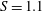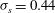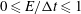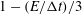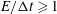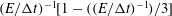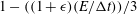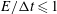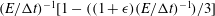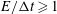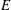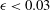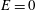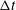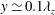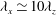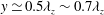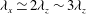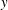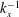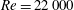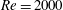Papers
Investigation of sheet-flow processes based on novel acoustic high-resolution velocity and concentration measurements
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 1-30
-
- Article
- Export citation
Fast transient microjets induced by hemispherical cavitation bubbles
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 31-51
-
- Article
- Export citation
Finite-amplitude acoustic-gravity waves: exact solutions
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 52-64
-
- Article
- Export citation
Effect of finite sampling time on estimation of Brownian fluctuation
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 65-84
-
- Article
- Export citation
Inertial effects on the generation of co-laminar flows
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 85-94
-
- Article
- Export citation
Dynamics of elastic dumbbells sedimenting in a viscous fluid: oscillations and hydrodynamic repulsion
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 95-108
-
- Article
- Export citation
Centre-manifold reduction of bifurcating flows
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 109-145
-
- Article
- Export citation
Azimuthal shear instability of a liquid jet injected into a gaseous cross-flow
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 146-172
-
- Article
- Export citation
Combustion enhancement in a scramjet engine using oxygen enrichment and porous fuel injection
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 173-198
-
- Article
- Export citation
Interacting vorticity waves as an instability mechanism for magnetohydrodynamic shear instabilities
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 199-225
-
- Article
- Export citation
Buoyancy-driven dispersion in a layered porous rock
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 226-239
-
- Article
- Export citation
The effect of seam imperfections on the unsteady flow within a fluid-filled torus
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 240-253
-
- Article
- Export citation
Statistical structure of self-sustaining attached eddies in turbulent channel flow
-
- Published online by Cambridge University Press:
- 12 February 2015, pp. 254-289
-
- Article
- Export citation
Dynamics of a binary mixture subjected to a temperature gradient and oscillatory forcing
-
- Published online by Cambridge University Press:
- 13 February 2015, pp. 290-322
-
- Article
- Export citation
Unsteady dynamics of rapid perching manoeuvres
-
- Published online by Cambridge University Press:
- 13 February 2015, pp. 323-341
-
- Article
- Export citation
Maximum kinetic energy dissipation and the stability of turbulent Poiseuille flow
-
- Published online by Cambridge University Press:
- 16 February 2015, pp. 342-363
-
- Article
- Export citation
Numerical simulations of three-dimensional plunging breaking waves: generation and evolution of aerated vortex filaments
-
- Published online by Cambridge University Press:
- 16 February 2015, pp. 364-393
-
- Article
- Export citation
Behaviour of a natural laminar flow aerofoil in flight through atmospheric turbulence
-
- Published online by Cambridge University Press:
- 16 February 2015, pp. 394-429
-
- Article
- Export citation
Maximizing the efficiency of a flexible propulsor using experimental optimization
-
- Published online by Cambridge University Press:
- 16 February 2015, pp. 430-448
-
- Article
- Export citation
The equilibrium dynamics and statistics of gravity–capillary waves
-
- Published online by Cambridge University Press:
- 18 February 2015, pp. 449-466
-
- Article
- Export citation