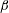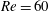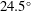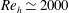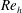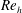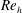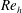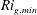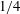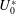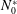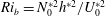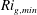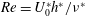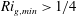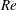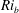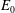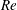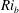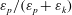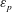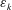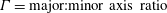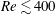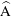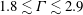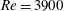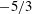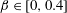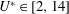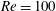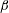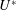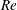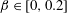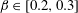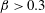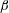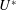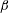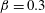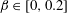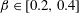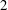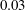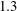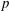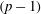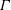The system composed of a circular cylinder, either fixed or elastically mounted, and immersed in a current linearly sheared in the cross-flow direction, is investigated via numerical simulations. The impact of the shear and associated symmetry breaking are explored over wide ranges of values of the shear parameter (non-dimensional inflow velocity gradient, 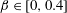 $\unicode[STIX]{x1D6FD}\in [0,0.4]$) and reduced velocity (inverse of the non-dimensional natural frequency of the oscillator,
$\unicode[STIX]{x1D6FD}\in [0,0.4]$) and reduced velocity (inverse of the non-dimensional natural frequency of the oscillator, 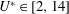 $U^{\ast }\in [2,14]$), at Reynolds number
$U^{\ast }\in [2,14]$), at Reynolds number 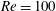 $Re=100$;
$Re=100$; 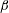 $\unicode[STIX]{x1D6FD}$,
$\unicode[STIX]{x1D6FD}$, 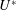 $U^{\ast }$ and
$U^{\ast }$ and 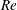 $Re$ are based on the inflow velocity at the centre of the body and on its diameter. In the absence of large-amplitude vibrations and in the fixed body case, three successive regimes are identified. Two unsteady flow regimes develop for
$Re$ are based on the inflow velocity at the centre of the body and on its diameter. In the absence of large-amplitude vibrations and in the fixed body case, three successive regimes are identified. Two unsteady flow regimes develop for 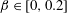 $\unicode[STIX]{x1D6FD}\in [0,0.2]$ (regime L) and
$\unicode[STIX]{x1D6FD}\in [0,0.2]$ (regime L) and 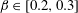 $\unicode[STIX]{x1D6FD}\in [0.2,0.3]$ (regime H). They differ by the relative influence of the shear, which is found to be limited in regime L. In contrast, the shear leads to a major reconfiguration of the wake (e.g. asymmetric pattern, lower vortex shedding frequency, synchronized oscillation of the saddle point) and a substantial alteration of the fluid forcing in regime H. A steady flow regime (S), characterized by a triangular wake pattern, is uncovered for
$\unicode[STIX]{x1D6FD}\in [0.2,0.3]$ (regime H). They differ by the relative influence of the shear, which is found to be limited in regime L. In contrast, the shear leads to a major reconfiguration of the wake (e.g. asymmetric pattern, lower vortex shedding frequency, synchronized oscillation of the saddle point) and a substantial alteration of the fluid forcing in regime H. A steady flow regime (S), characterized by a triangular wake pattern, is uncovered for 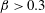 $\unicode[STIX]{x1D6FD}>0.3$. Free vibrations of large amplitudes arise in a region of the parameter space that encompasses the entire range of
$\unicode[STIX]{x1D6FD}>0.3$. Free vibrations of large amplitudes arise in a region of the parameter space that encompasses the entire range of 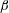 $\unicode[STIX]{x1D6FD}$ and a range of
$\unicode[STIX]{x1D6FD}$ and a range of 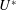 $U^{\ast }$ that widens as
$U^{\ast }$ that widens as 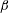 $\unicode[STIX]{x1D6FD}$ increases; therefore vibrations appear beyond the limit of steady flow in the fixed body case (
$\unicode[STIX]{x1D6FD}$ increases; therefore vibrations appear beyond the limit of steady flow in the fixed body case (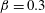 $\unicode[STIX]{x1D6FD}=0.3$). Three distinct regimes of the flow–structure system are encountered in this region. In all regimes, body motion and flow unsteadiness are synchronized (lock-in condition). For
$\unicode[STIX]{x1D6FD}=0.3$). Three distinct regimes of the flow–structure system are encountered in this region. In all regimes, body motion and flow unsteadiness are synchronized (lock-in condition). For 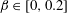 $\unicode[STIX]{x1D6FD}\in [0,0.2]$, in regime VL, the system behaviour remains close to that observed in uniform current. The main impact of the shear concerns the amplification of the in-line response and the transition from figure-eight to ellipsoidal orbits. For
$\unicode[STIX]{x1D6FD}\in [0,0.2]$, in regime VL, the system behaviour remains close to that observed in uniform current. The main impact of the shear concerns the amplification of the in-line response and the transition from figure-eight to ellipsoidal orbits. For 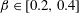 $\unicode[STIX]{x1D6FD}\in [0.2,0.4]$, the system exhibits two well-defined regimes: VH1 and VH2 in the lower and higher ranges of
$\unicode[STIX]{x1D6FD}\in [0.2,0.4]$, the system exhibits two well-defined regimes: VH1 and VH2 in the lower and higher ranges of 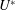 $U^{\ast }$, respectively. Even if the wake patterns, close to the asymmetric pattern observed in regime H, are comparable in both regimes, the properties of the vibrations and fluid forces clearly depart. The responses differ by their spectral contents, i.e. sinusoidal versus multi-harmonic, and their amplitudes are much larger in regime VH1, where the in-line responses reach
$U^{\ast }$, respectively. Even if the wake patterns, close to the asymmetric pattern observed in regime H, are comparable in both regimes, the properties of the vibrations and fluid forces clearly depart. The responses differ by their spectral contents, i.e. sinusoidal versus multi-harmonic, and their amplitudes are much larger in regime VH1, where the in-line responses reach 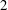 $2$ diameters (
$2$ diameters (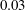 $0.03$ diameters in uniform flow) and the cross-flow responses
$0.03$ diameters in uniform flow) and the cross-flow responses 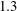 $1.3$ diameters. Aperiodic, intermittent oscillations are found to occur in the transition region between regimes VH1 and VH2; it appears that wake–body synchronization persists in this case.
$1.3$ diameters. Aperiodic, intermittent oscillations are found to occur in the transition region between regimes VH1 and VH2; it appears that wake–body synchronization persists in this case.