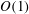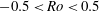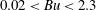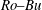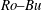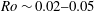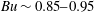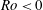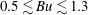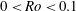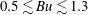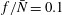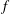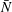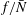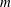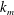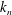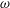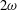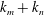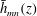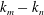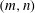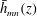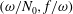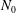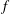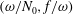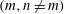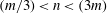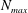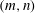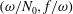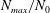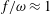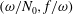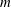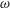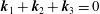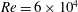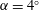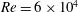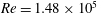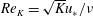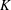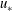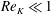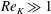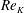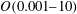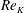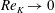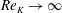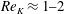We present a theoretical study of nonlinear effects that result from modal interactions in internal waves in a non-uniformly stratified finite-depth fluid with background rotation. A linear wave field containing modes 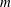 $m$ and
$m$ and  $n$ (of horizontal wavenumbers
$n$ (of horizontal wavenumbers 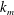 $k_{m}$ and
$k_{m}$ and 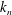 $k_{n}$) at a fixed frequency
$k_{n}$) at a fixed frequency 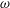 $\unicode[STIX]{x1D714}$ results in two different terms in the steady-state weakly nonlinear solution: (i) a superharmonic wave of frequency
$\unicode[STIX]{x1D714}$ results in two different terms in the steady-state weakly nonlinear solution: (i) a superharmonic wave of frequency 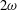 $2\unicode[STIX]{x1D714}$, horizontal wavenumber
$2\unicode[STIX]{x1D714}$, horizontal wavenumber 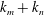 $k_{m}+k_{n}$ and a vertical structure
$k_{m}+k_{n}$ and a vertical structure 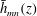 $\bar{h}_{mn}(z)$ and (ii) a time-independent term (Eulerian mean flow) with horizontal wavenumber
$\bar{h}_{mn}(z)$ and (ii) a time-independent term (Eulerian mean flow) with horizontal wavenumber 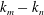 $k_{m}-k_{n}$. For some
$k_{m}-k_{n}$. For some 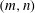 $(m,n)$,
$(m,n)$, 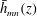 $\bar{h}_{mn}(z)$ is infinitely large along specific curves on the
$\bar{h}_{mn}(z)$ is infinitely large along specific curves on the 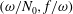 $(\unicode[STIX]{x1D714}/N_{0},f/\unicode[STIX]{x1D714})$ plane, where
$(\unicode[STIX]{x1D714}/N_{0},f/\unicode[STIX]{x1D714})$ plane, where 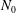 $N_{0}$ and
$N_{0}$ and 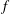 $f$ are the deep ocean stratification and the Coriolis frequency, respectively; these curves are referred to as divergence curves in the rest of this paper. In uniform stratifications, a unique divergence curve occurs on the
$f$ are the deep ocean stratification and the Coriolis frequency, respectively; these curves are referred to as divergence curves in the rest of this paper. In uniform stratifications, a unique divergence curve occurs on the 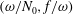 $(\unicode[STIX]{x1D714}/N_{0},f/\unicode[STIX]{x1D714})$ plane for those
$(\unicode[STIX]{x1D714}/N_{0},f/\unicode[STIX]{x1D714})$ plane for those 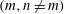 $(m,n\neq m)$ that satisfy
$(m,n\neq m)$ that satisfy 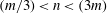 $(m/3)<n<(3m)$. In the presence of a pycnocline (whose strength is quantified by the maximum stratification
$(m/3)<n<(3m)$. In the presence of a pycnocline (whose strength is quantified by the maximum stratification 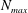 $N_{max}$), divergence curves occur for several more modal interactions than those for a uniform stratification; furthermore, a given
$N_{max}$), divergence curves occur for several more modal interactions than those for a uniform stratification; furthermore, a given 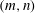 $(m,n)$ interaction can result in multiple divergence curves on the
$(m,n)$ interaction can result in multiple divergence curves on the 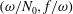 $(\unicode[STIX]{x1D714}/N_{0},f/\unicode[STIX]{x1D714})$ plane for a fixed
$(\unicode[STIX]{x1D714}/N_{0},f/\unicode[STIX]{x1D714})$ plane for a fixed 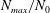 $N_{max}/N_{0}$. Nearby high-mode interactions in a uniform stratification and any modal interaction in a non-uniform stratification with a sufficiently strong pycnocline are shown to result in near-horizontal divergence curves around
$N_{max}/N_{0}$. Nearby high-mode interactions in a uniform stratification and any modal interaction in a non-uniform stratification with a sufficiently strong pycnocline are shown to result in near-horizontal divergence curves around 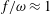 $f/\unicode[STIX]{x1D714}\approx 1$, thus implying that strong nonlinear effects often occur as a result of interaction within triads containing two different modes at the near-inertial frequency. Notably, self-interaction of certain modes in a non-uniform stratification results in one or more divergence curves on the
$f/\unicode[STIX]{x1D714}\approx 1$, thus implying that strong nonlinear effects often occur as a result of interaction within triads containing two different modes at the near-inertial frequency. Notably, self-interaction of certain modes in a non-uniform stratification results in one or more divergence curves on the 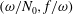 $(\unicode[STIX]{x1D714}/N_{0},f/\unicode[STIX]{x1D714})$ plane, thus suggesting that even arbitrarily small-amplitude individual modes cannot remain linear in a non-uniform stratification. We show that internal wave resonant triads containing modes
$(\unicode[STIX]{x1D714}/N_{0},f/\unicode[STIX]{x1D714})$ plane, thus suggesting that even arbitrarily small-amplitude individual modes cannot remain linear in a non-uniform stratification. We show that internal wave resonant triads containing modes 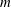 $m$ and
$m$ and  $n$ at frequency
$n$ at frequency 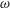 $\unicode[STIX]{x1D714}$ occur along the divergence curves, and their existence is guaranteed upon the satisfaction of two different criteria: (i) the horizontal component of the standard triadic resonance criterion
$\unicode[STIX]{x1D714}$ occur along the divergence curves, and their existence is guaranteed upon the satisfaction of two different criteria: (i) the horizontal component of the standard triadic resonance criterion 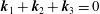 $\boldsymbol{k}_{1}+\boldsymbol{k}_{2}+\boldsymbol{k}_{3}=0$ and (ii) a non-orthogonality criterion. For uniform stratifications, criterion (ii) reduces to the vertical component of the standard triadic resonance criterion. For non-uniform stratifications, criterion (ii) seems to be always satisfied whenever criterion (i) is satisfied, thus significantly increasing the number of modal interactions that result in strong nonlinear effects irrespective of the wave amplitudes. We then adapt our theoretical framework to identify resonant triads and hence provide insights into the generation of higher harmonics in two different oceanic scenarios: (i) low-mode internal tide propagating over small- or large-scale topography and (ii) an internal wave beam incident on a pycnocline in the upper ocean, for which our results are in qualitative agreement with the numerical study of Diamessis et al. (Dynam. Atmos. Oceans., vol. 66, 2014, pp. 110–137).
$\boldsymbol{k}_{1}+\boldsymbol{k}_{2}+\boldsymbol{k}_{3}=0$ and (ii) a non-orthogonality criterion. For uniform stratifications, criterion (ii) reduces to the vertical component of the standard triadic resonance criterion. For non-uniform stratifications, criterion (ii) seems to be always satisfied whenever criterion (i) is satisfied, thus significantly increasing the number of modal interactions that result in strong nonlinear effects irrespective of the wave amplitudes. We then adapt our theoretical framework to identify resonant triads and hence provide insights into the generation of higher harmonics in two different oceanic scenarios: (i) low-mode internal tide propagating over small- or large-scale topography and (ii) an internal wave beam incident on a pycnocline in the upper ocean, for which our results are in qualitative agreement with the numerical study of Diamessis et al. (Dynam. Atmos. Oceans., vol. 66, 2014, pp. 110–137).