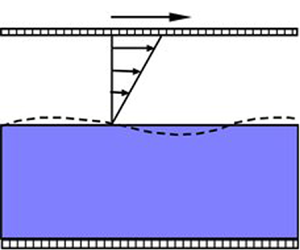
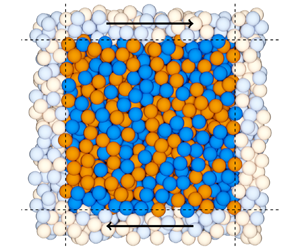
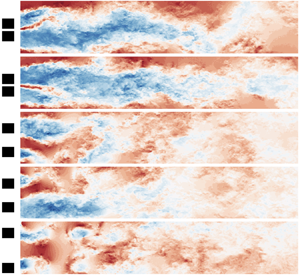
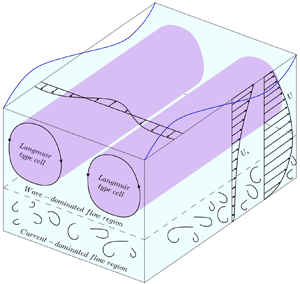
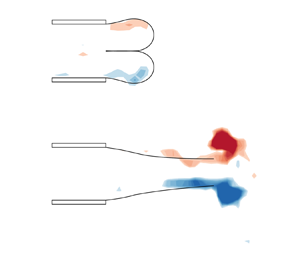
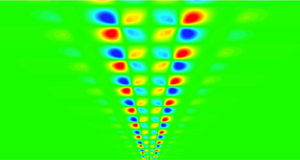
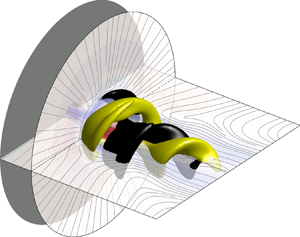
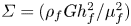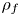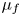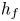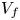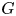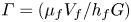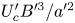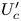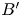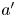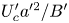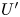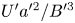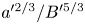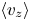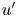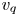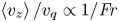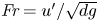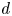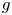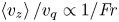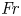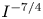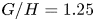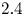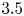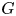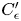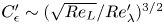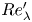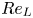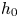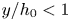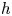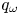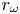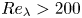Graphical abstract from Wüthrich, D., Shi, R. & Chanson, H. 2021 Strong free-surface turbulence in breaking bores: a physical study on the free-surface dynamics and air-water interfacial features. J. Fluid Mech.924, A20. doi:10.1017/jfm.2021.614.
JFM Perspectives
Stability and the transition to turbulence in the flow through conduits with compliant walls
-
- Published online by Cambridge University Press:
- 05 August 2021, P1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
On the Boussinesq approximation in arbitrarily accelerating frames of reference
-
- Published online by Cambridge University Press:
- 11 August 2021, R1
-
- Article
- Export citation
Stationary electro-osmotic flow driven by AC fields around charged dielectric spheres
-
- Published online by Cambridge University Press:
- 11 August 2021, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Additional spanwise vortices near the free surface in open channel flows
-
- Published online by Cambridge University Press:
- 12 August 2021, R3
-
- Article
- Export citation
Focus on Fluids
Extending the reach of Lagrangian analysis in turbulence
-
- Published online by Cambridge University Press:
- 10 August 2021, F1
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
A macrotransport equation for the Hele-Shaw flow of a concentrated suspension
-
- Published online by Cambridge University Press:
- 09 August 2021, A1
-
- Article
- Export citation
The effect of nonlinear drag on the rise velocity of bubbles in turbulence
-
- Published online by Cambridge University Press:
- 04 August 2021, A2
-
- Article
- Export citation
Drag, diffusion and segregation in inertial granular flows
-
- Published online by Cambridge University Press:
- 04 August 2021, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A turbulence dissipation inhomogeneity scaling in the wake of two side-by-side square prisms
-
- Published online by Cambridge University Press:
- 04 August 2021, A4
-
- Article
- Export citation
Correlation-based flow decomposition and statistical analysis of the eddy forcing
-
- Published online by Cambridge University Press:
- 04 August 2021, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the influence of collinear surface waves on turbulence in smooth-bed open-channel flows
-
- Published online by Cambridge University Press:
- 04 August 2021, A6
-
- Article
- Export citation
Starting jet formation through eversion of elastic sheets
-
- Published online by Cambridge University Press:
- 04 August 2021, A7
-
- Article
- Export citation
Distributed vortex-wave interactions: the relation of self-similarity to the attached eddy hypothesis
-
- Published online by Cambridge University Press:
- 04 August 2021, A8
-
- Article
- Export citation
Closing the loop: nonlinear Taylor vortex flow through the lens of resolvent analysis
-
- Published online by Cambridge University Press:
- 04 August 2021, A9
-
- Article
- Export citation
Transition from shear-dominated to Rayleigh–Taylor turbulence
-
- Published online by Cambridge University Press:
- 05 August 2021, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reynolds-number scaling of a vorticity-annihilating boundary layer
-
- Published online by Cambridge University Press:
- 06 August 2021, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The relation between wave asymmetry and particle orbits analysed by Slepian models
-
- Published online by Cambridge University Press:
- 05 August 2021, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local vortex line topology and geometry in turbulence
-
- Published online by Cambridge University Press:
- 05 August 2021, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear dynamics of fully developed swirling jets
-
- Published online by Cambridge University Press:
- 05 August 2021, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Plumes in rotating fluid and their transformation into tornados
-
- Published online by Cambridge University Press:
- 05 August 2021, A15
-
- Article
- Export citation